Понимание многоугольников: классификация и характеристики фигур
Многоугольники — это геометрические фигуры, состоящие из конечного числа отрезков, соединенных в замкнутую линию. Важно уметь классифицировать многоугольники по количеству сторон и углов. В этой статье мы собрали полезные советы для лучшего понимания этой темы, чтобы вы могли легко различать и идентифицировать различные типы многоугольников.
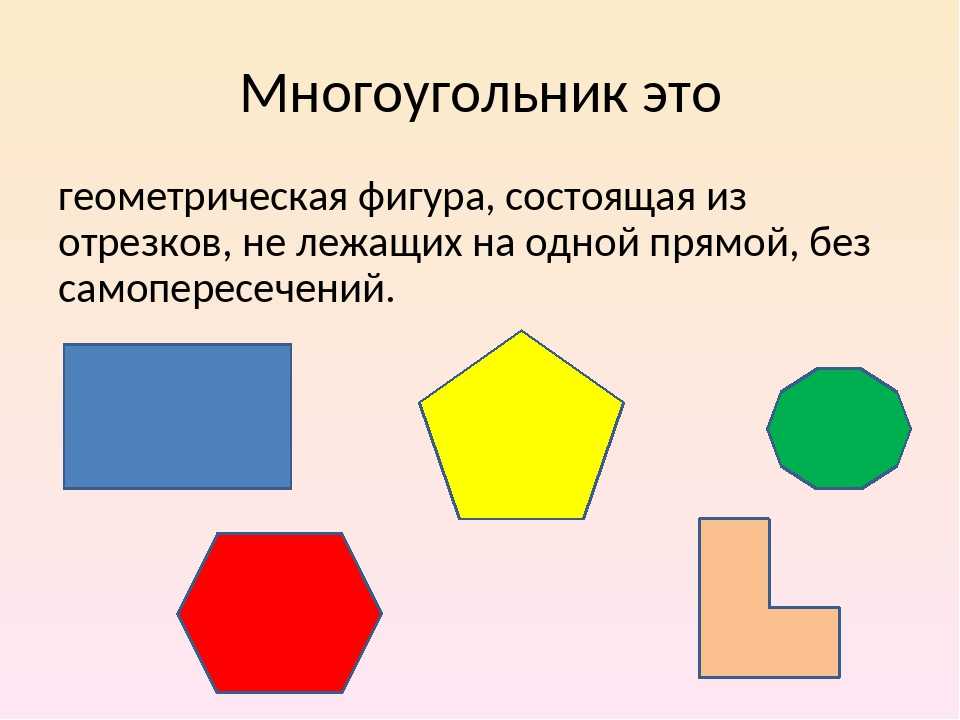
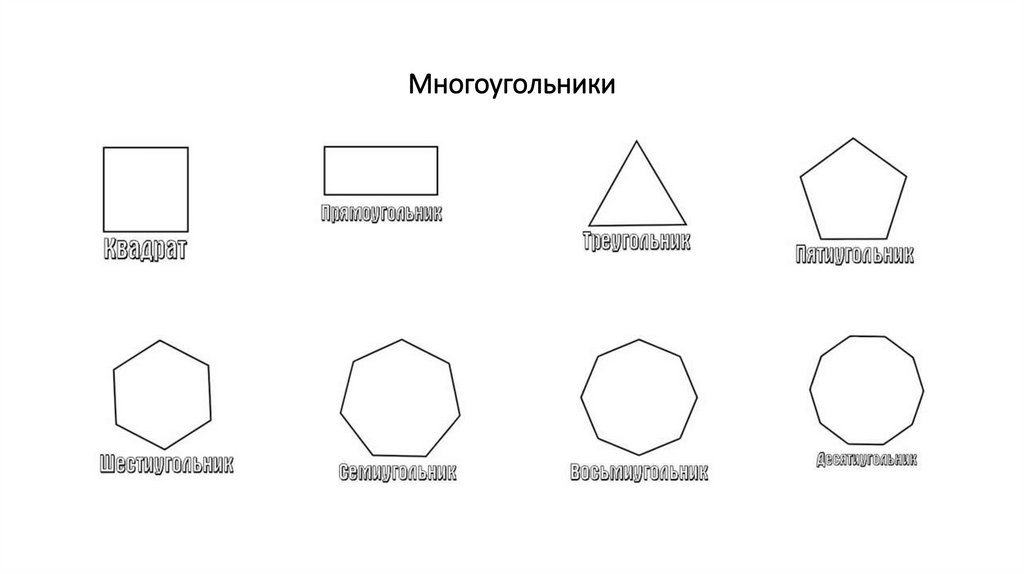
Обратите внимание на количество сторон: каждое многоугольник имеет определенное число сторон, которое важно для его классификации.

Геометрия 8 класс. Многоугольники
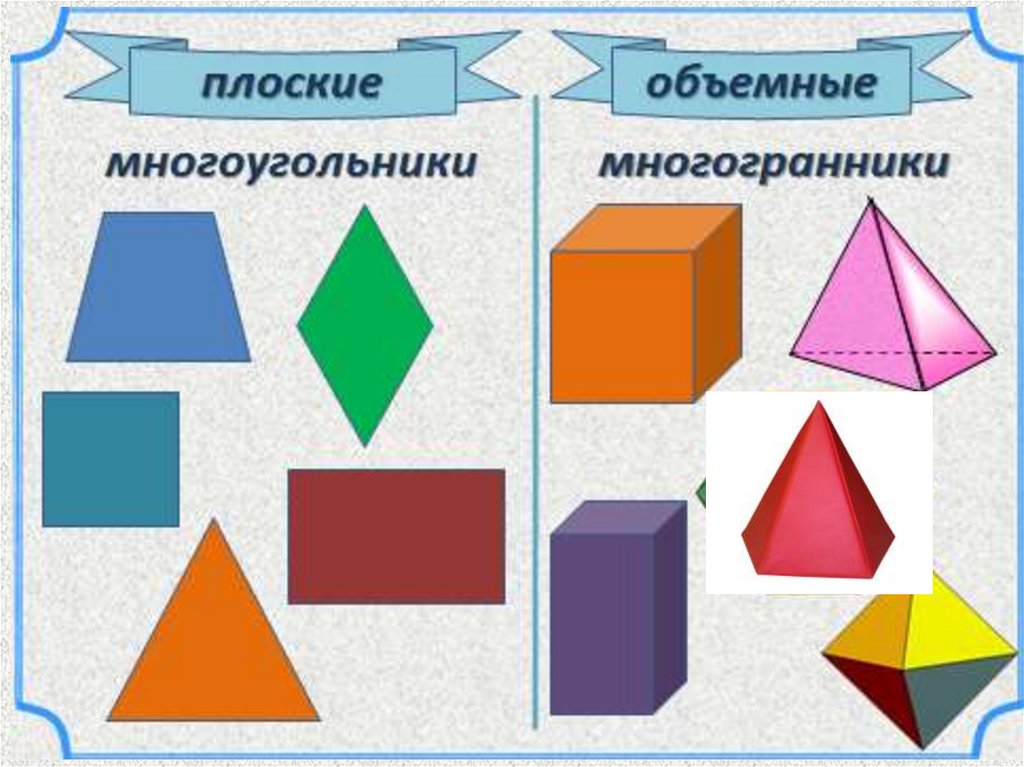
Для классификации многоугольников можно использовать такие термины, как треугольник, четырехугольник, пятиугольник и так далее.

Геометрия. 7 класс. Урок 7 \

Важно учитывать, что все углы в правильном многоугольнике равны, что помогает легко вычислить его внутренние углы.

Правильные многоугольники. Геометрия 9 класс - Математика - TutorOnline
Запомните, что если все стороны многоугольника равны, это правильный многоугольник, а если стороны разные — неправильный.

Многоугольники. 8 класс.
При изучении многоугольников не забывайте о их диагоналях — отрезках, соединяющих не смежные вершины фигуры.
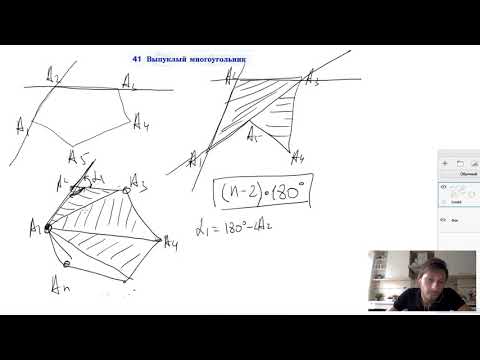
41. Выпуклый многоугольник

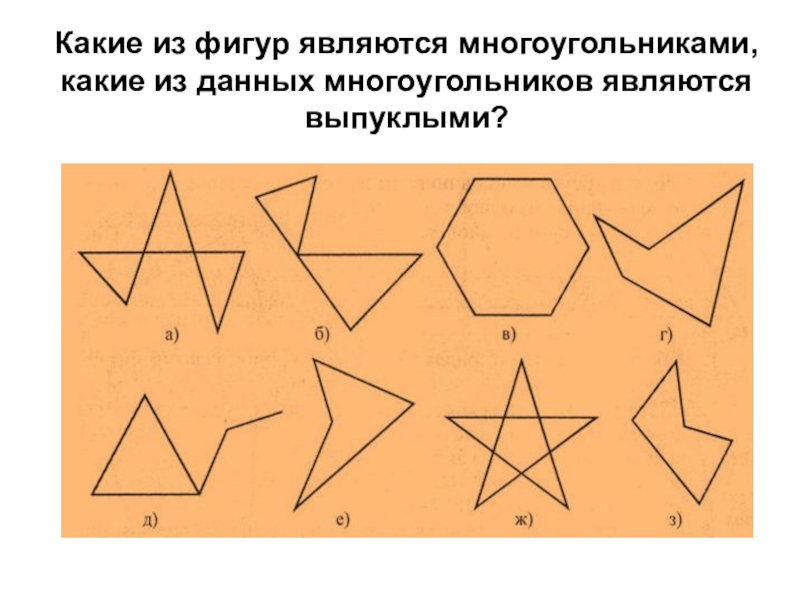
Существует особая категория многоугольников — выпуклые, где все их углы меньше 180 градусов.

Подобие многоугольников
Прямоугольник — это особый вид четырехугольника с четырьмя прямыми углами, и его противоположные стороны всегда равны.

Математика 5 класс. Треугольники. Многоугольники
Чтобы проверить, является ли многоугольник правильным, нужно удостовериться, что все его стороны и углы одинаковы.

Многоугольник
Для правильных многоугольников есть формула для вычисления суммы внутренних углов: (n-2) * 180°, где n — количество сторон.

Многоугольники. Равные фигуры. 5 класс

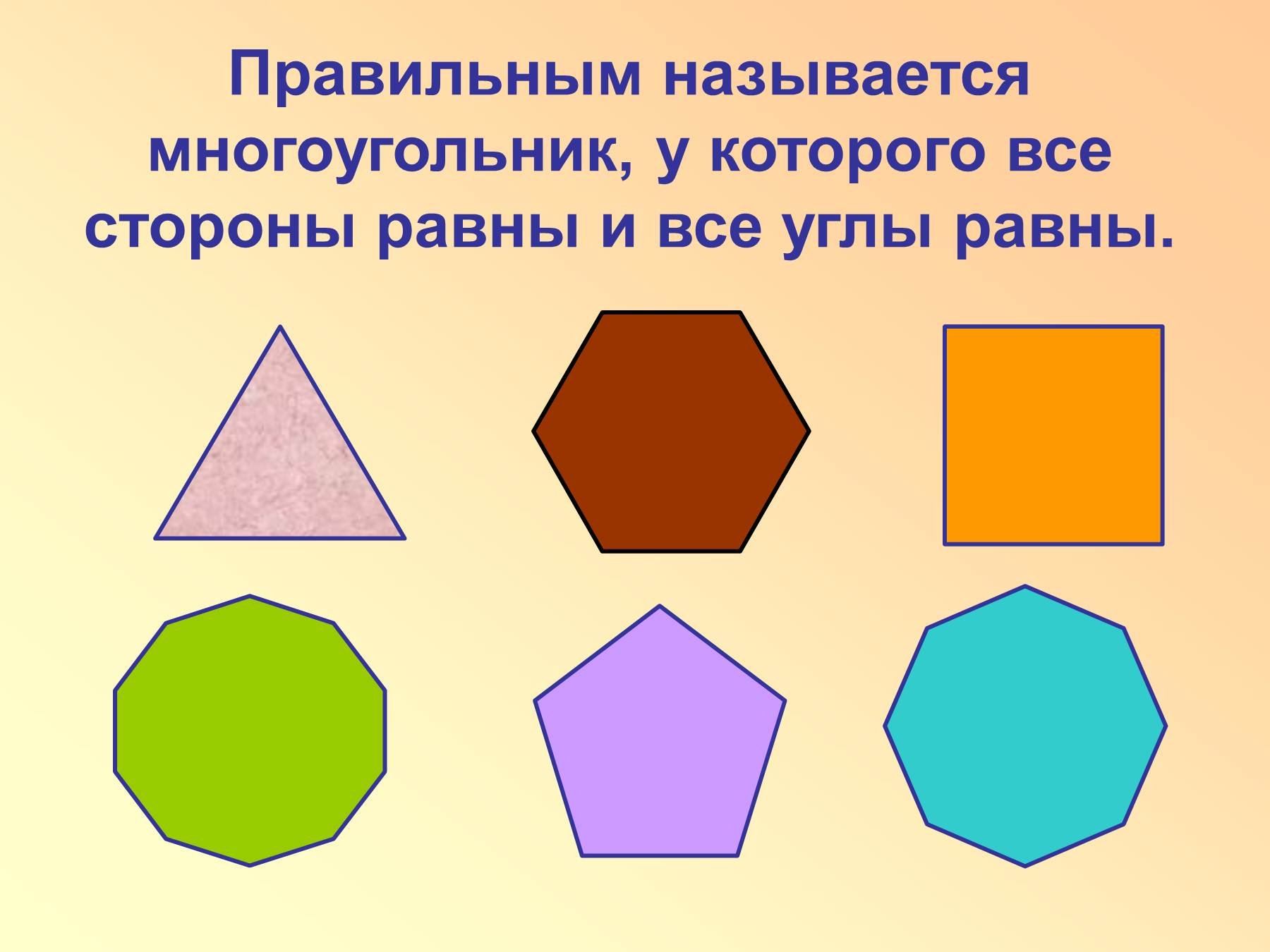
Изучая многоугольники, обращайте внимание на их симметрию — регулярные многоугольники всегда имеют оси симметрии, которые проходят через их вершины.


Классный способ для разметки любого угла без транспортира.