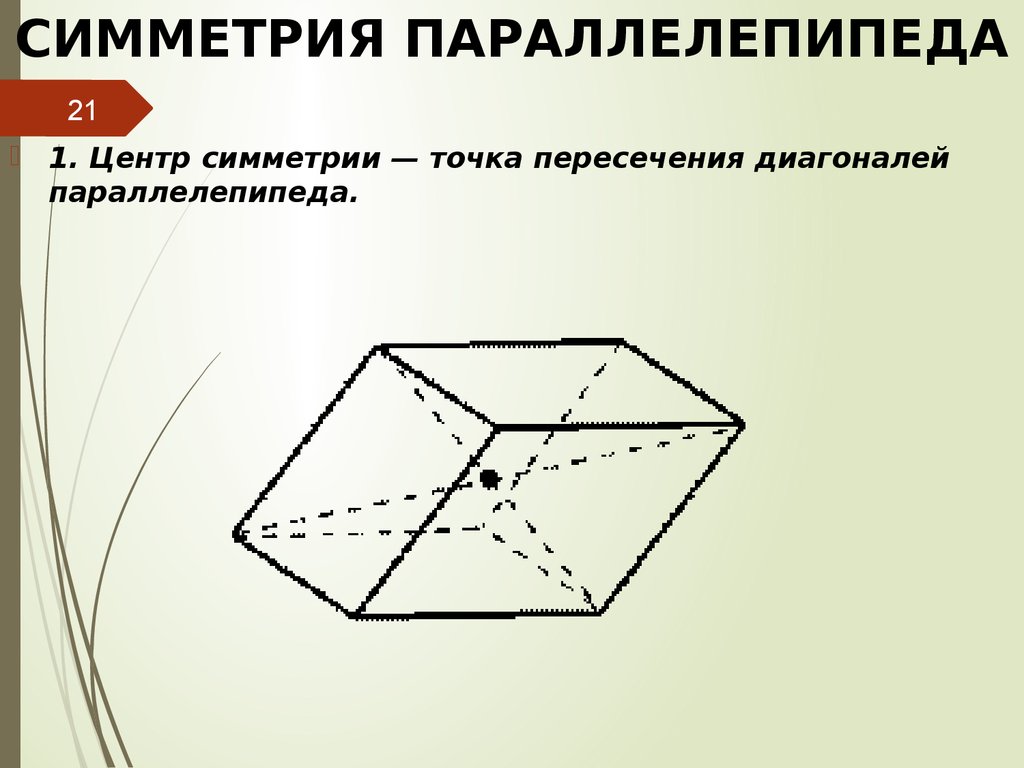
Основные аспекты симметрии параллелепипеда: от теории к практике

Элементы симметрии параллелепипеда имеют важное значение в геометрии и математике. Эти элементы включают оси симметрии, плоскости симметрии и центры симметрии, которые определяют его форму и особенности. Изучение симметрии помогает лучше понять пространственные структуры и их преобразования, что находит применение в различных областях науки и инженерии.

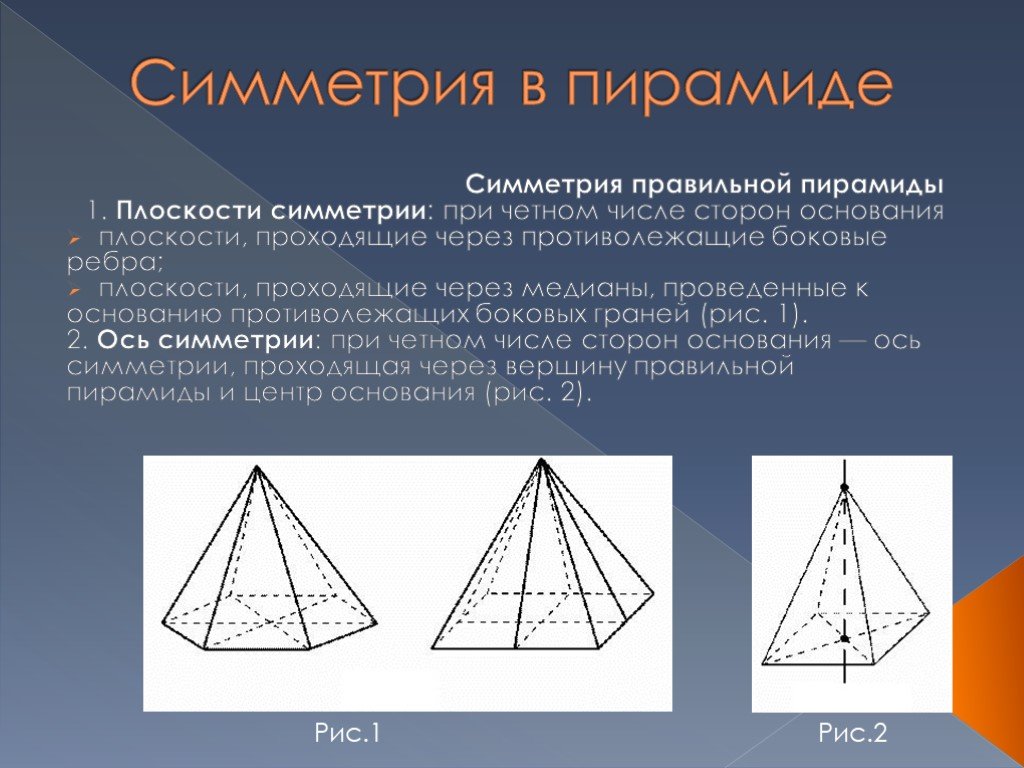
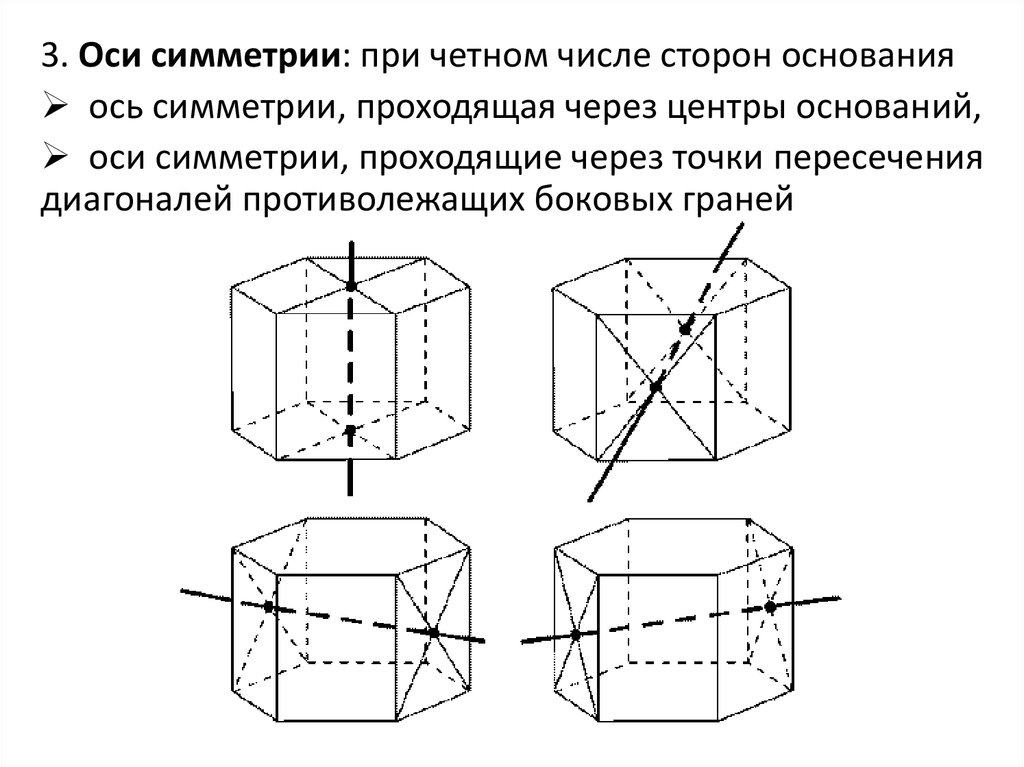
Для начала важно разобраться, что параллелепипед имеет 3 оси симметрии, проходящие через его середины противоположных граней.

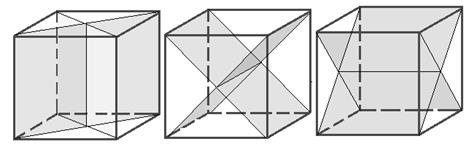
При изучении симметрии параллелепипеда следует обращать внимание на его диагонали — они также могут служить осями симметрии в некоторых случаях.

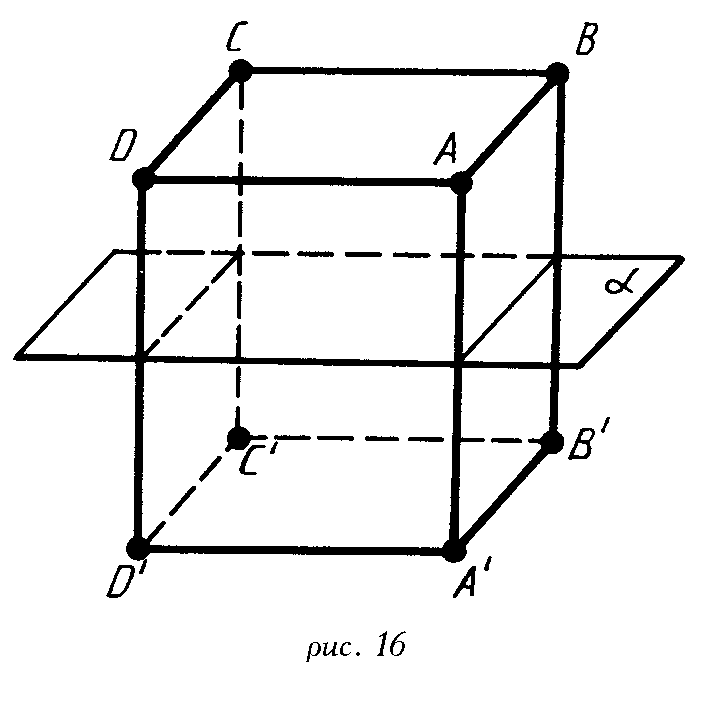
Для практических задач полезно представить параллелепипед как результат пересечения двух прямоугольных кубов, что поможет увидеть все его симметричные особенности.

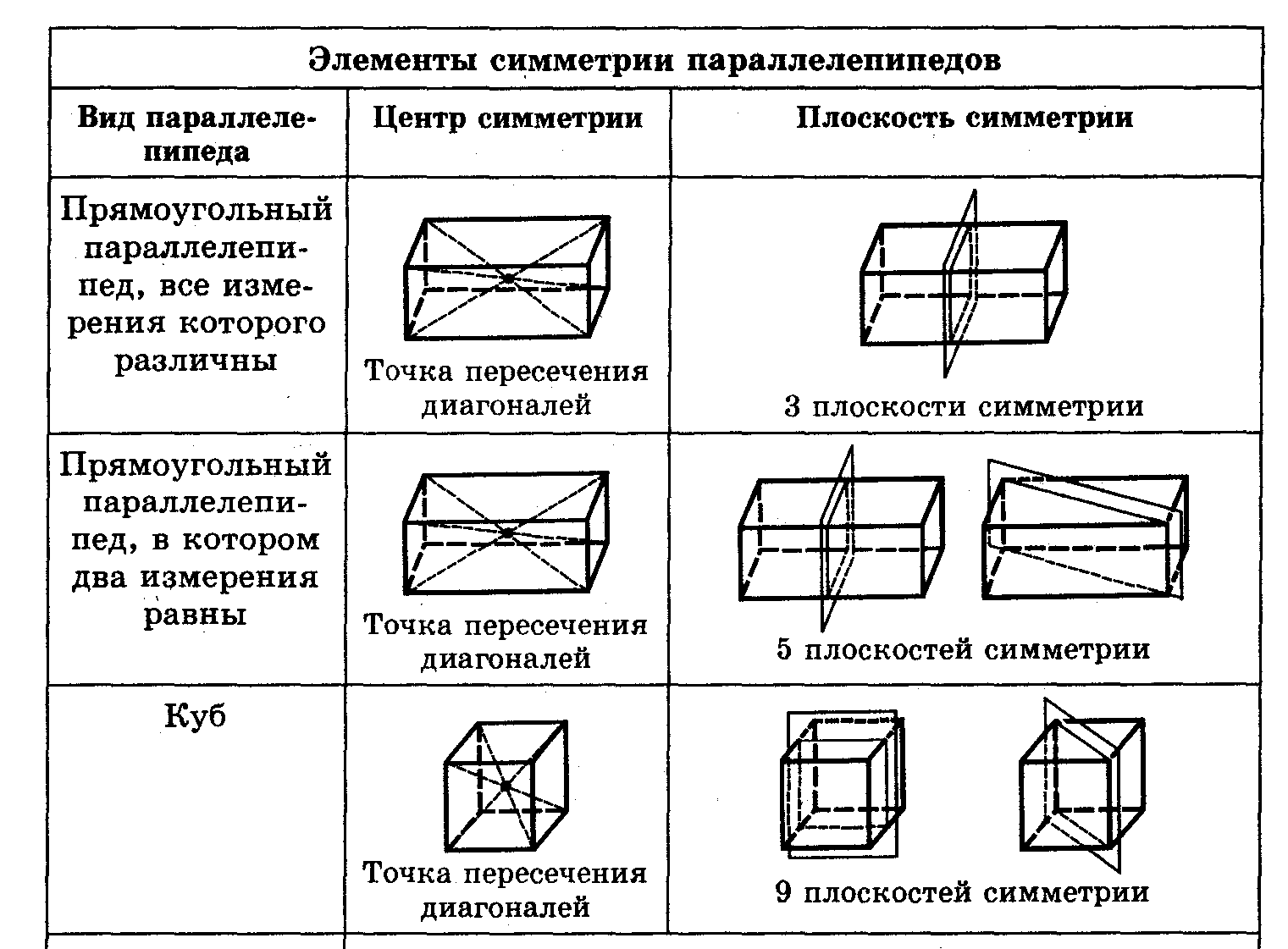
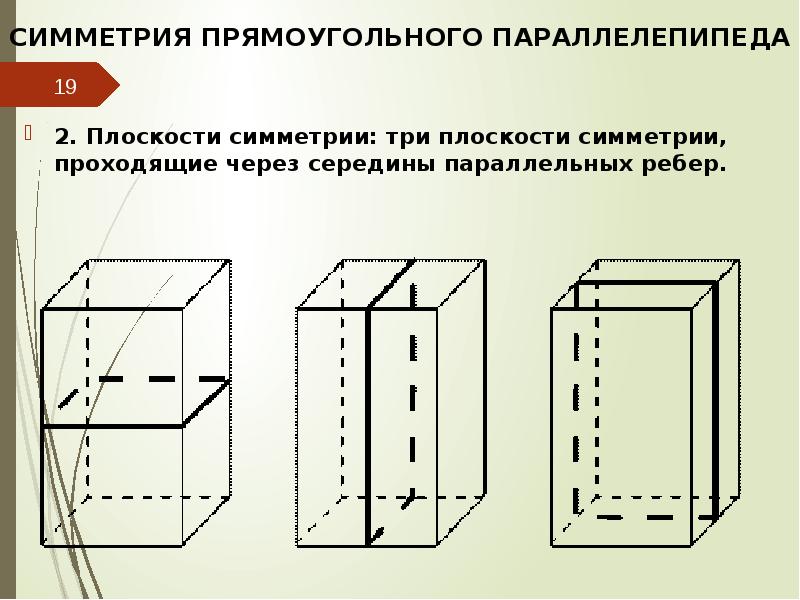
При проектировании объектов, основанных на параллелепипедах, полезно использовать зеркальную симметрию для оптимизации форм и упрощения вычислений.

Симметричные элементы параллелепипеда могут быть использованы для создания устойчивых конструкций в инженерии и архитектуре.

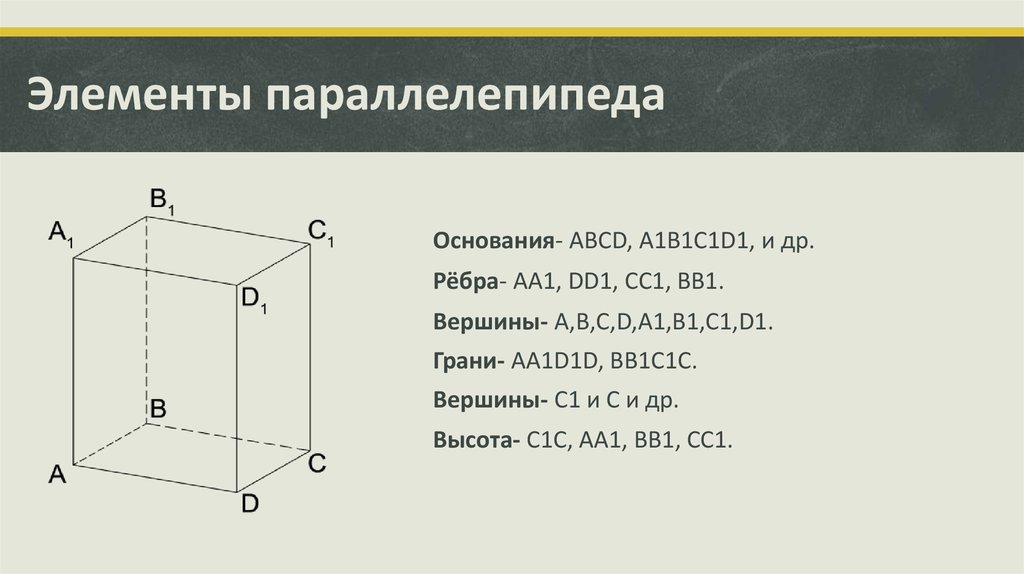
Для более точного представления симметрии параллелепипеда, рисуйте его в 3D-проекции, что поможет визуализировать оси и плоскости симметрии.

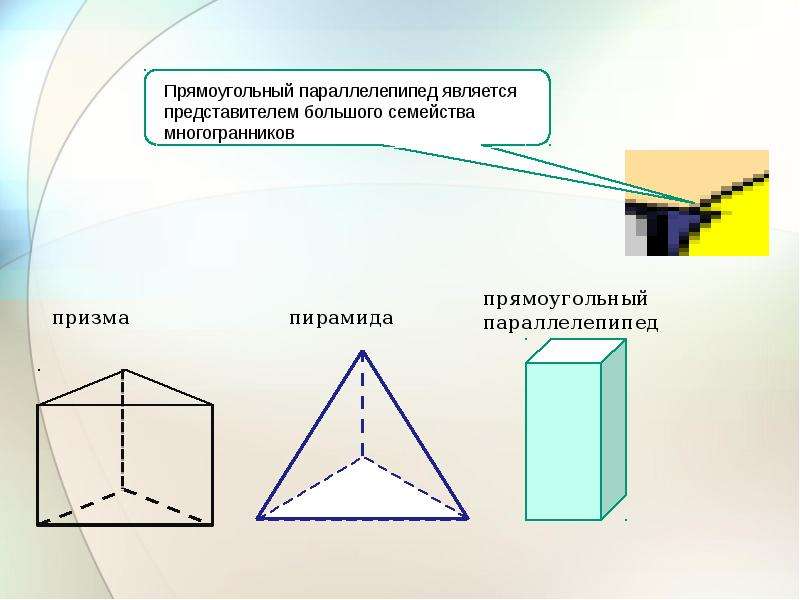
Симметрия параллелепипеда может быть полезна при решении задач на равновесие или распределение нагрузок в физических системах.

Применяйте знания о симметрии параллелепипеда для изучения других многогранников — многие их свойства будут аналогичны.

Для более глубокого понимания используйте компьютерные модели и симуляции, чтобы наглядно изучить поведение симметричных объектов в различных ситуациях.

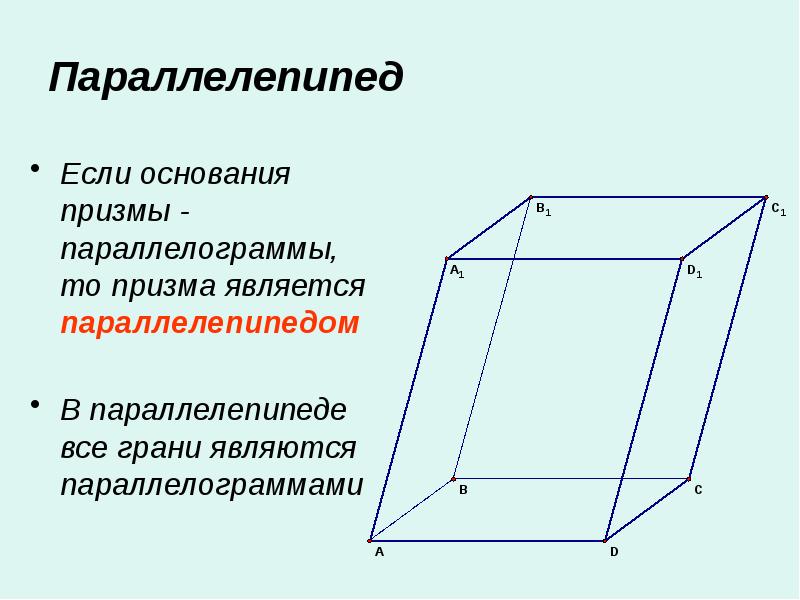
Не забывайте, что элементы симметрии могут значительно ускорить вычисления в задачах на геометрические преобразования и преобразования координат.