Понимание элементарных формул в математической логике и их роль в решении задач
На данной странице собраны фотографии, иллюстрирующие ключевые понятия элементарных формул в математической логике, а также полезные советы, которые помогут вам лучше понять и применить эти формулы для решения задач.

Изучайте элементарные логические операции, такие как конъюнкция, дизъюнкция и импликация, так как они являются основой для более сложных формул.

Таблица истинности

Не забывайте, что правильное использование скобок в формулах математической логики критично для корректного определения их смысла.

Классическая логика. Элементы математической логики.

Рекомендуется научиться визуализировать логические выражения, что поможет легче их анализировать и интерпретировать.

Типы логических формул

Практикуйтесь на простых примерах, чтобы глубже понять принципы работы с элементарными логическими формулами.

Конъюнкция, дизъюнкция, импликация, эквиваленция, отрицание. На примерах из жизни. Логика.
Использование таблиц истинности поможет вам наглядно оценивать правильность логических выражений.

Схема решения задач в математической логике

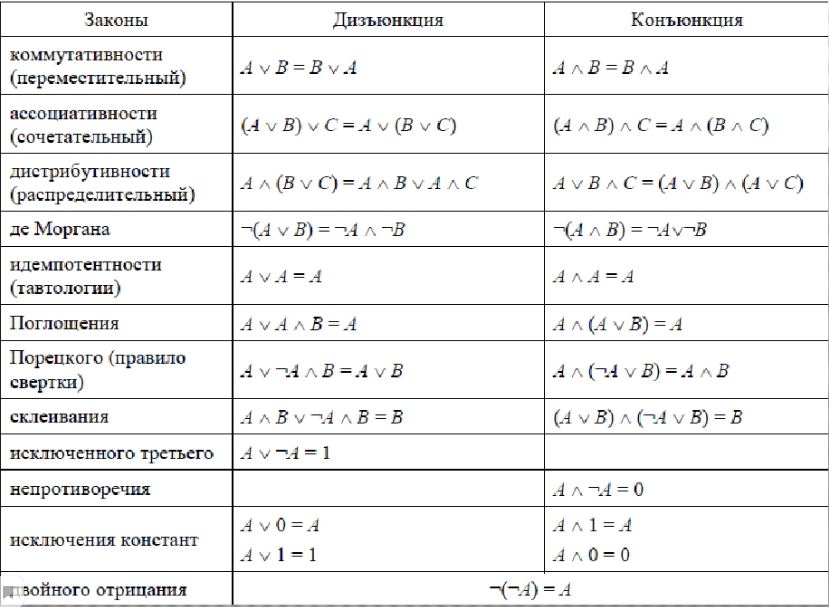
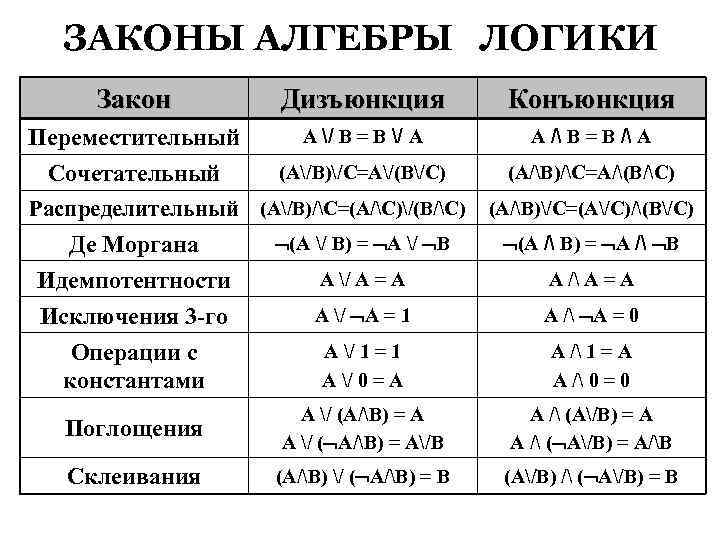
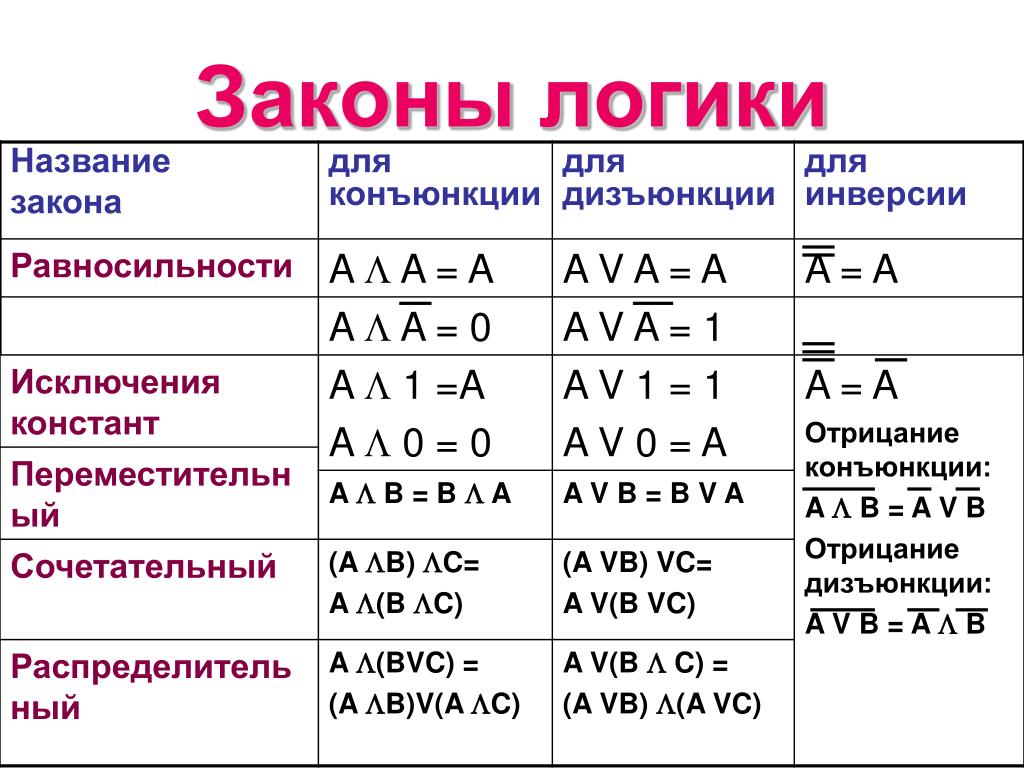
Обратите внимание на законы логики, такие как закон двойного отрицания и дистрибутивность, которые облегчают работу с формулами.
Попробуйте решать задачи на доказательства, применяя элементарные логические формулы для укрепления навыков.

Изучение теории доказательств поможет вам лучше понять, как элементарные формулы используются для логических выводов.

Синтаксис формул логики высказываний


Создавайте собственные логические выражения для тренировки и закрепления теоретических знаний.


Не забывайте проверять свои решения, используя разные методы доказательства и анализа логических формул.

Преобразование логических выражений / Упрощение выражений (практика) [Алгебра логики] #6