Основы работы с прямыми и призмами в геометрии: практическое руководство
На данной странице мы собрали полезные советы и фотографии, которые помогут вам лучше понять, как работать с геометрическими конструкциями, такими как прямые и призмы, используя пример а1а2а3. Эти материалы помогут вам освоить основные принципы построения и анализа таких объектов, а также дадут практические рекомендации для решения задач.


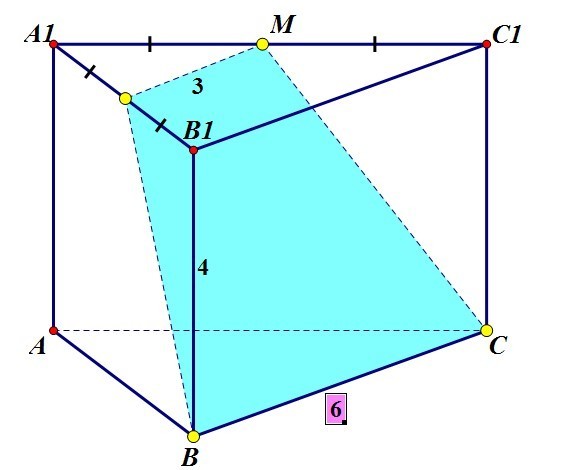
При работе с прямыми и призмами важно правильно определить их взаимное расположение и соотношение сторон для точного построения.

Площадь поверхности призмы. 11 класс.

Для более точных расчетов рекомендуется использовать вспомогательные линии и углы, которые помогут вам точно определить позиции точек.

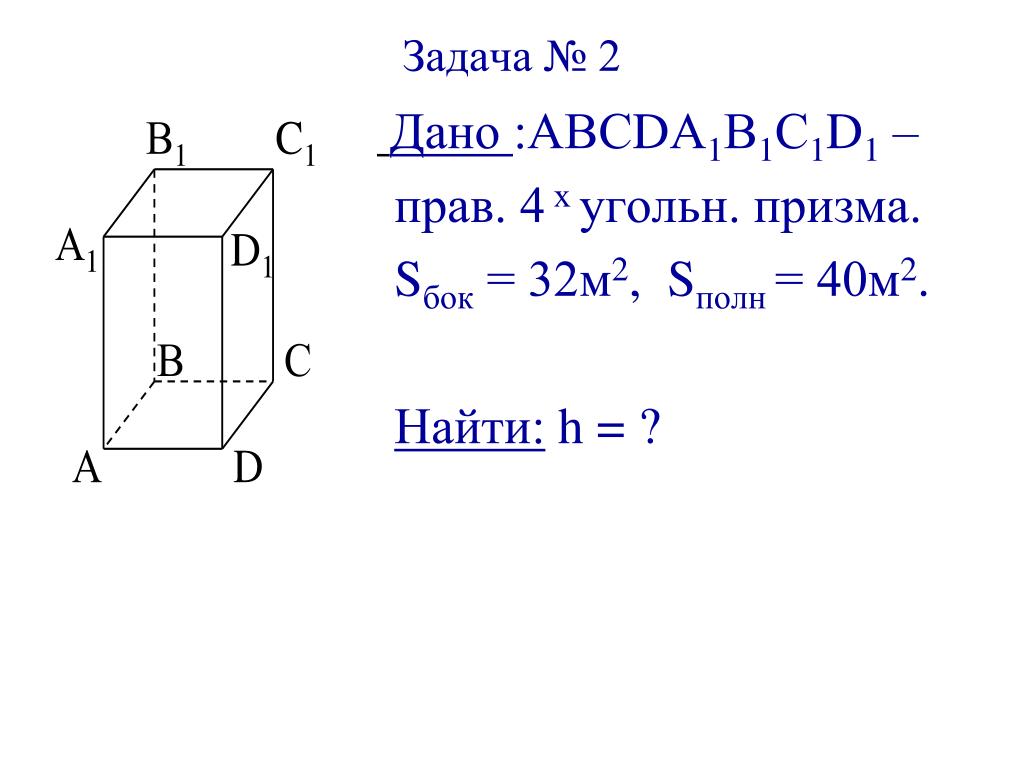
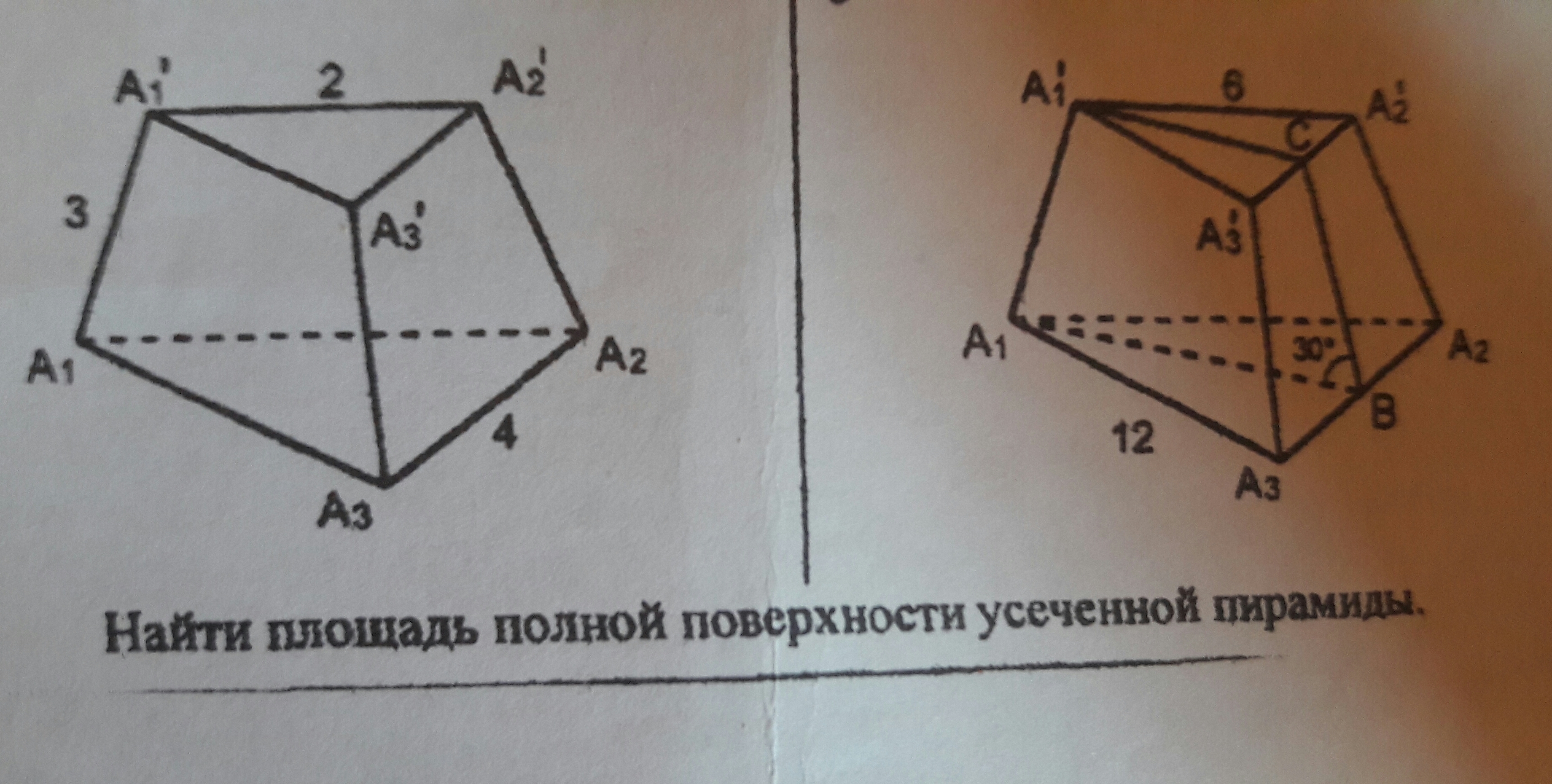
Задание 11. Объём и площадь поверхности составного многогранника.
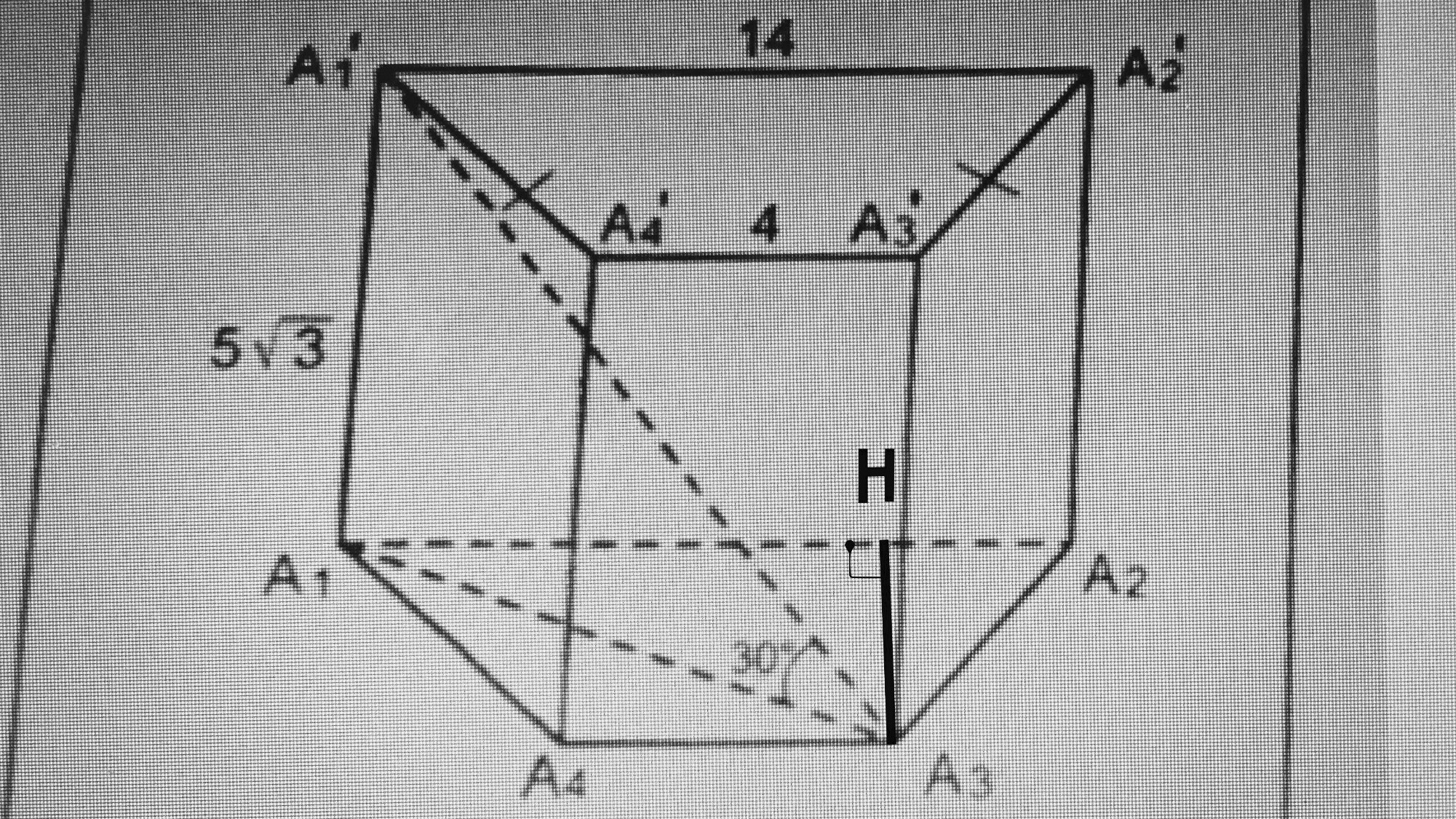

Если в задаче присутствуют несколько объектов, всегда следите за их соотношением в масштабе, чтобы избежать ошибок при построении.

Реакция на результаты ЕГЭ 2022 по русскому языку

Перед началом построения геометрической фигуры всегда рисуйте предварительные чертежи, чтобы избежать ошибок в дальнейшем.
Площадь поверхности многогранника

Использование различных методов измерения углов и длин поможет вам точнее определить параметры прямых и призм в задаче.
КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?
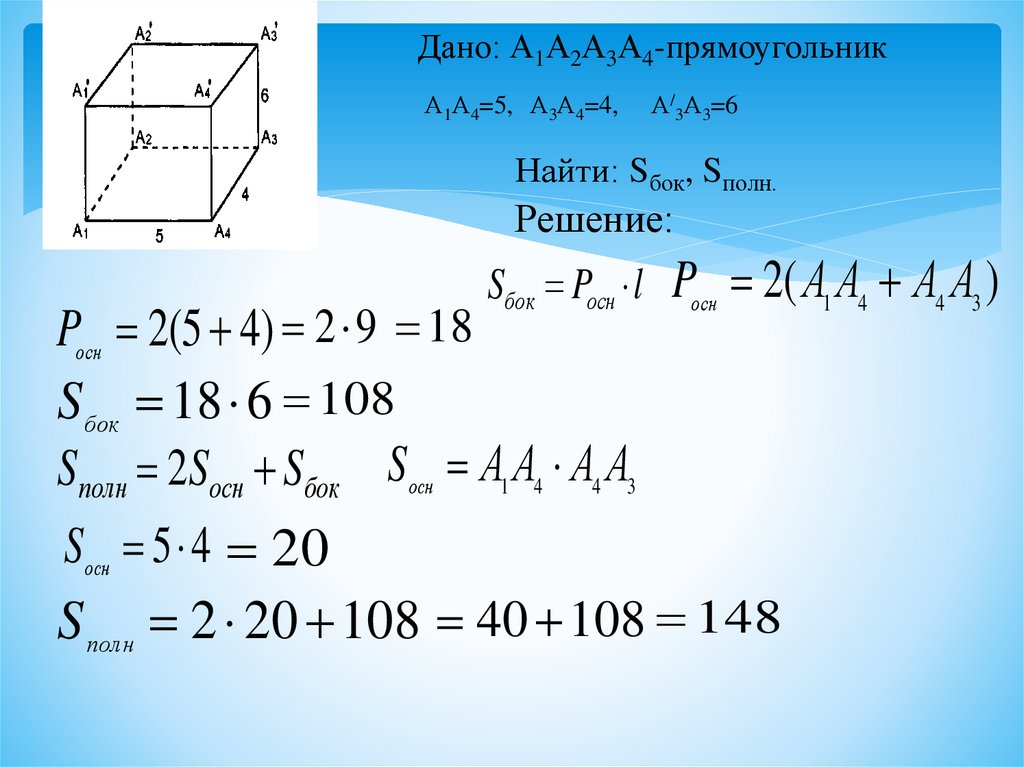
Для проверки правильности построения можно использовать симметрию и зеркальные отражения, что поможет избежать геометрических неточностей.
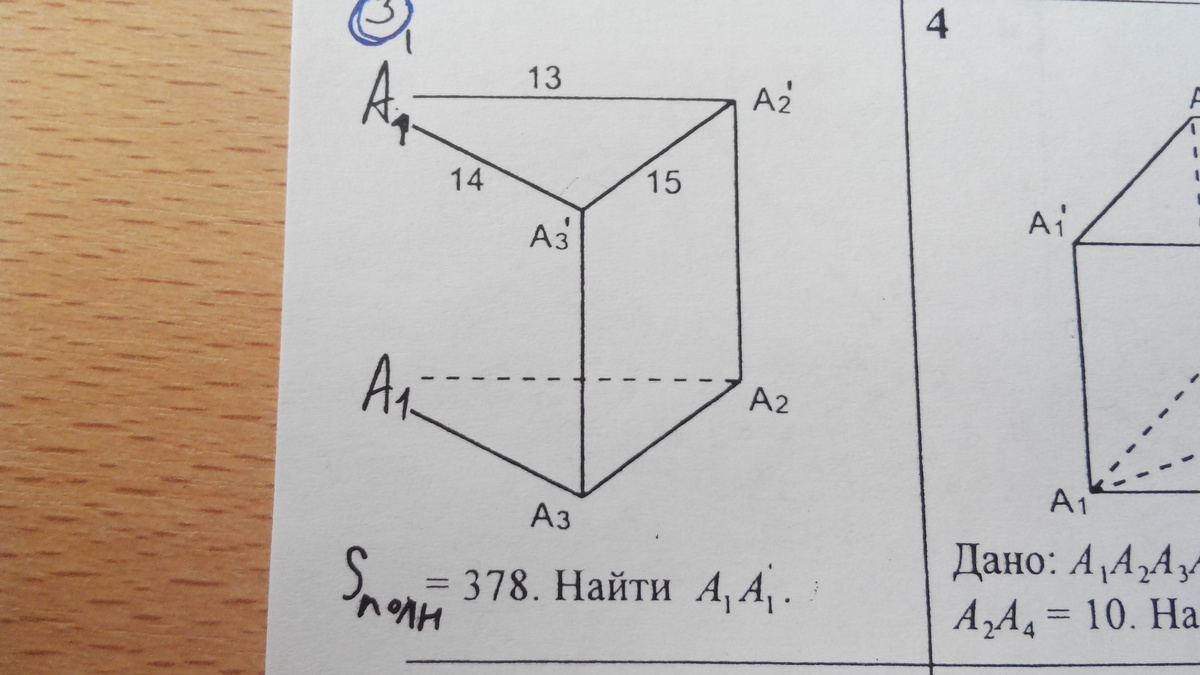
Внимательно следите за единицами измерения при вычислениях, чтобы не допустить ошибку в расчетах длин и углов.
Использование программных средств для построения геометрических фигур может значительно упростить работу и уменьшить количество ошибок.

тип 3. ЕГЭ профиль. № 1F4550 Площадь боковой поверхности треугольной призмы равна
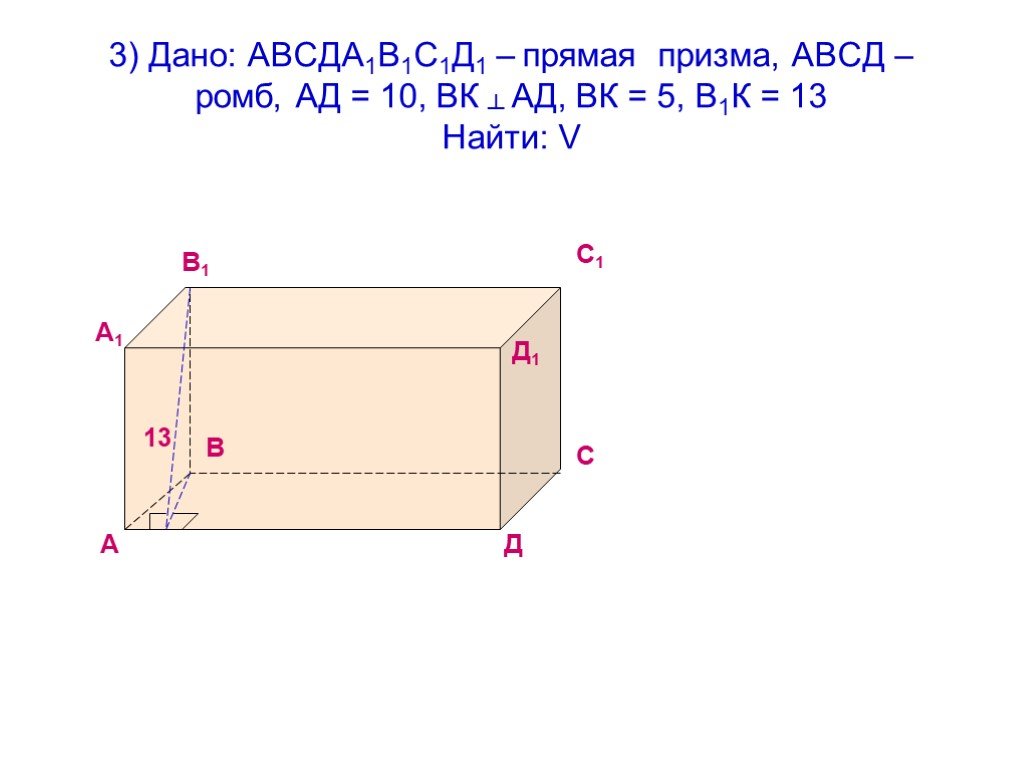
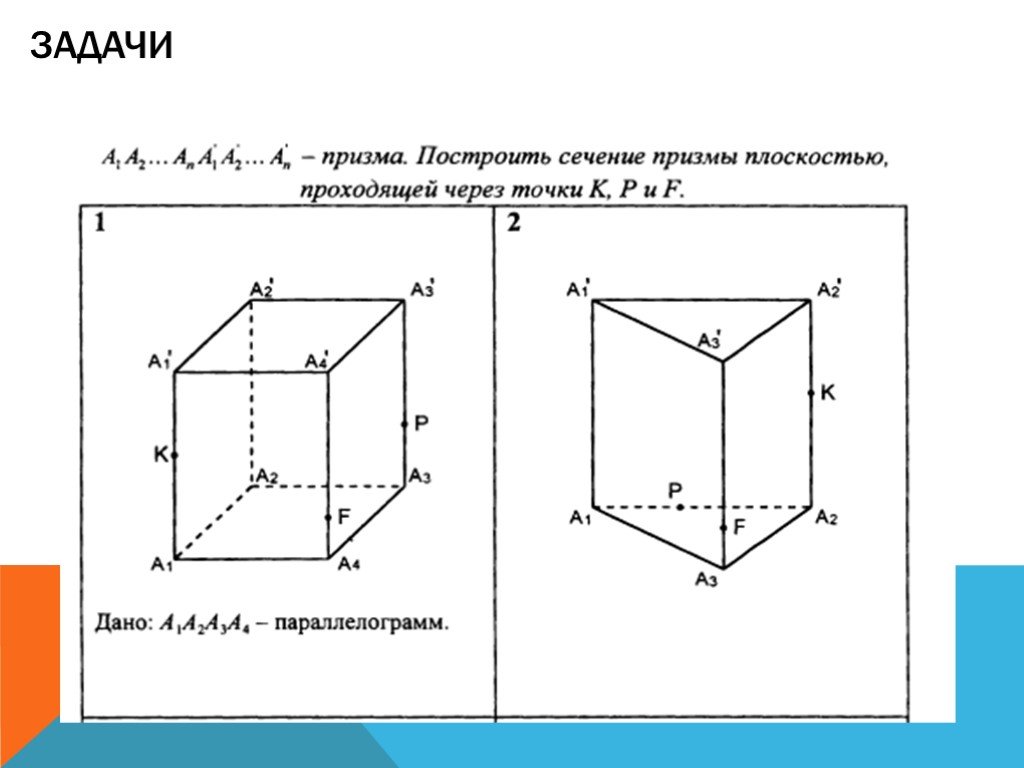
При анализе фигур всегда проверяйте взаимное расположение точек и сторон, что поможет вам быстрее обнаружить возможные ошибки в построении.
Не забывайте, что точность и аккуратность при выполнении геометрических построений – залог правильного результата.

Как найти объем многогранника? / Задача из ЕГЭ #25579