Как значение производной функции помогает анализировать её поведение на различных интервалах
Значение производной функции в каждой точке интервала — это важнейший элемент математического анализа, который помогает понять, как функция изменяется в каждой точке. Производная даёт информацию о скорости изменения функции и её локальных характеристиках. В этой подборке собраны советы, которые помогут вам разобраться в этом фундаментальном понятии и научиться эффективно использовать его для анализа графиков и решения задач.
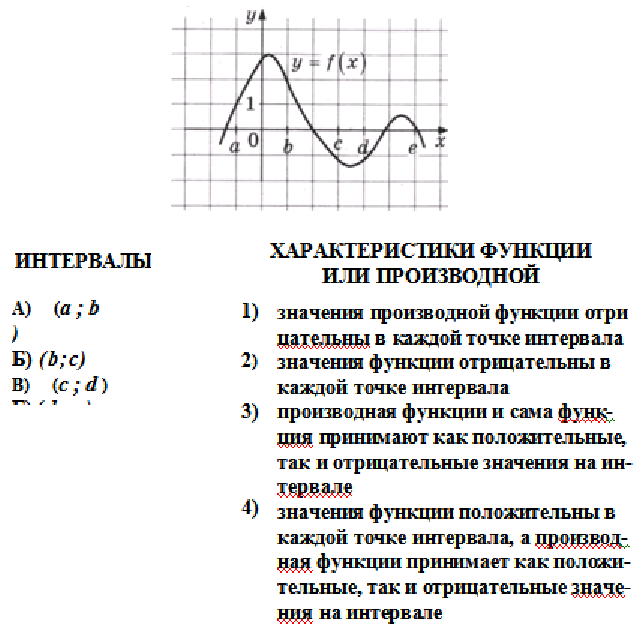

Для правильного понимания значения производной важно знать, что она может быть как положительной, так и отрицательной, что влияет на направление изменения функции.
Задание 14 базового ЕГЭ по математике. Функции. На рисунке изображён график y =f(х)
Производная функции в каждой точке интервала показывает скорость её изменения, и если она равна нулю, это может означать экстремум функции на данном участке.

Найти интервалы выпуклости и точки перегиба графика функции
Чтобы найти критические точки функции, нужно решить уравнение, в котором производная функции равна нулю или не существует.
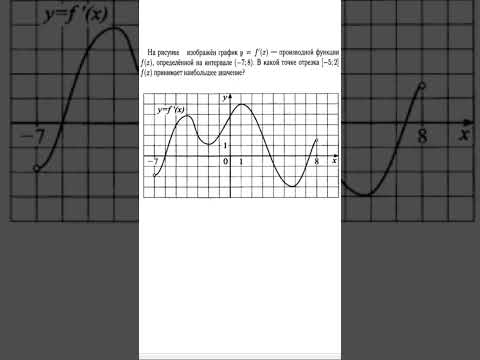
График производной функции. 8 задание профиля. #егэ #математика #профиль#производная #экстремум
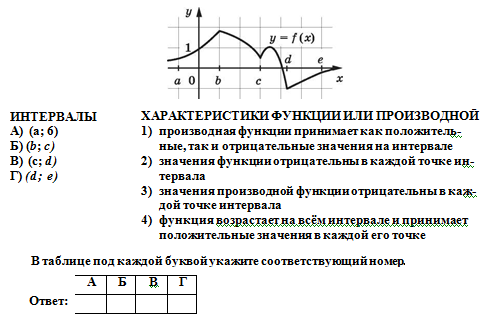
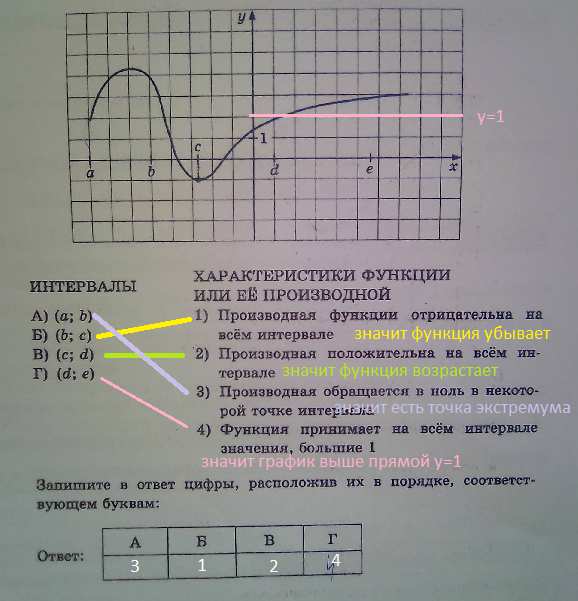
Изучая поведение функции с помощью её производной, можно определить интервалы роста и убыли функции, что значительно упрощает анализ её графика.
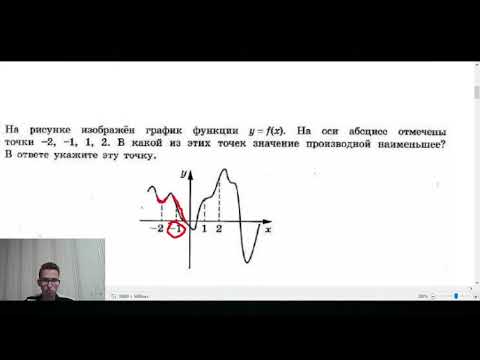
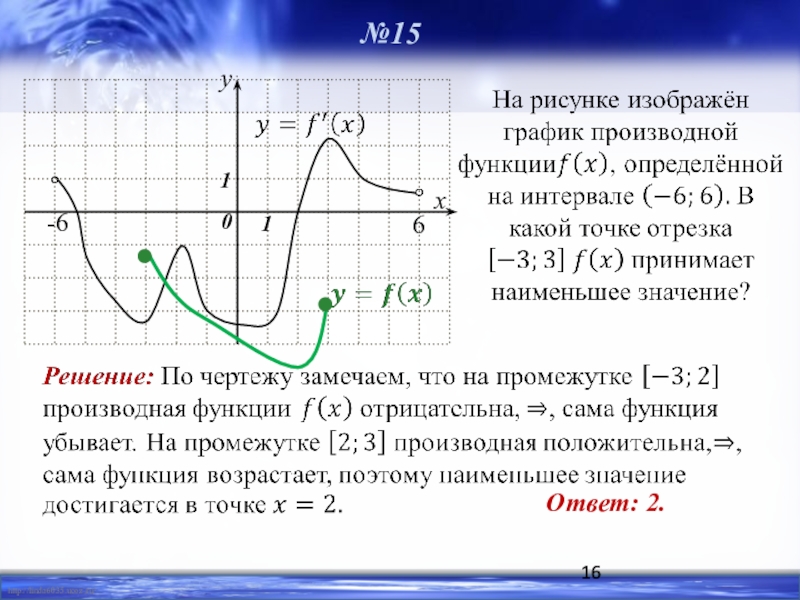
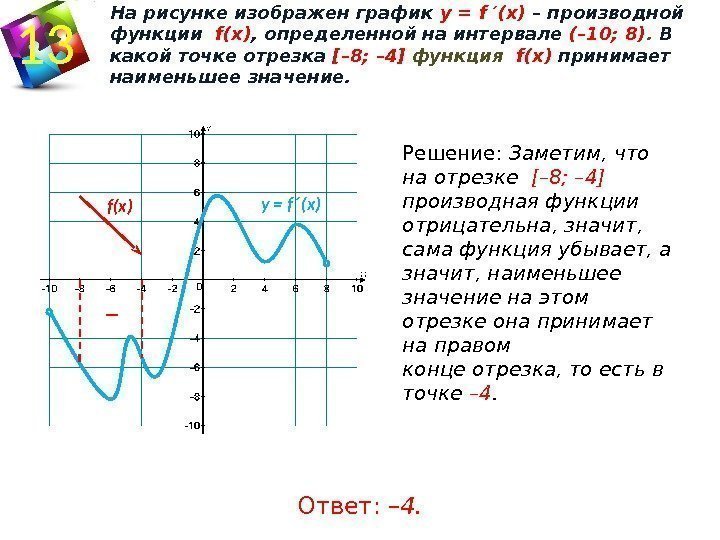
В какой точке значение ПРОИЗВОДНОЙ наименьшее?
Если производная функции меняет знак, это может свидетельствовать о наличии экстремума (максимума или минимума) в данной точке.

Тема 2 Пример на нахождение значения производной функции в точке
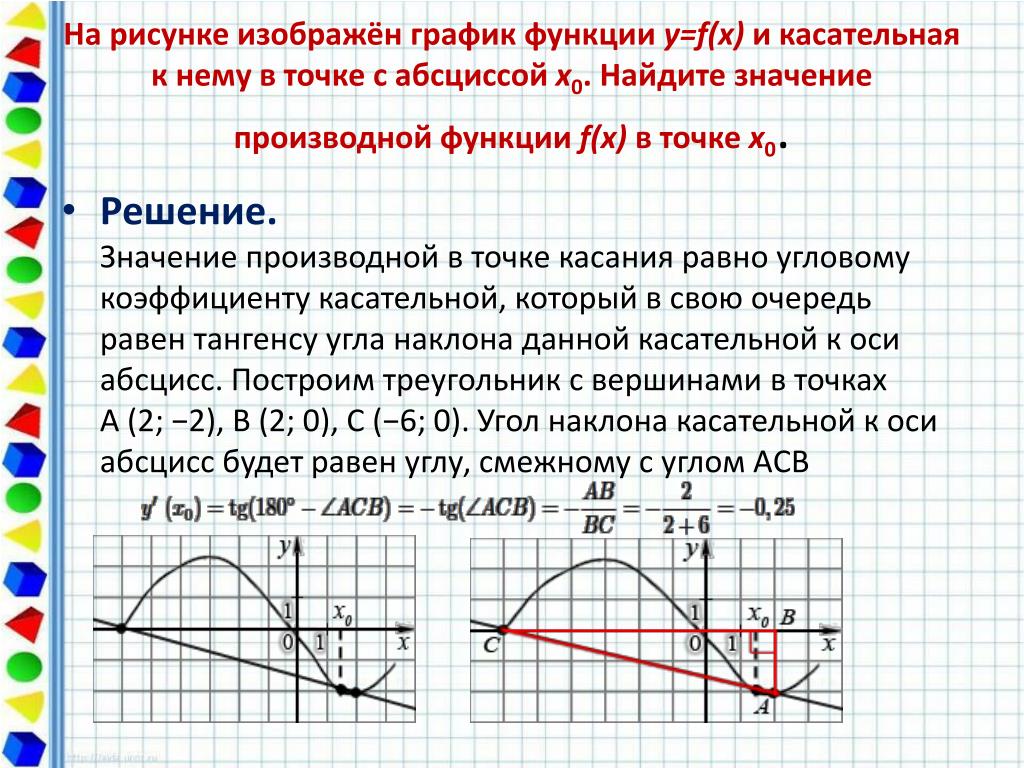
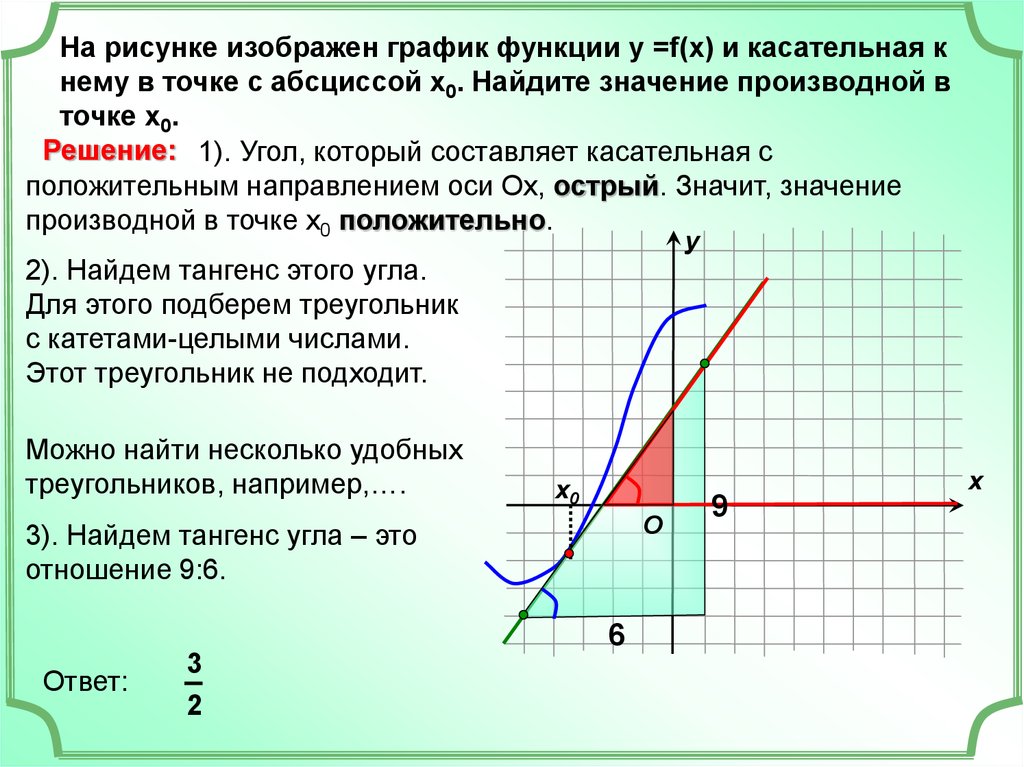
Значение производной также важно для определения касательной к графику функции в данной точке: наклон касательной равен значению производной.
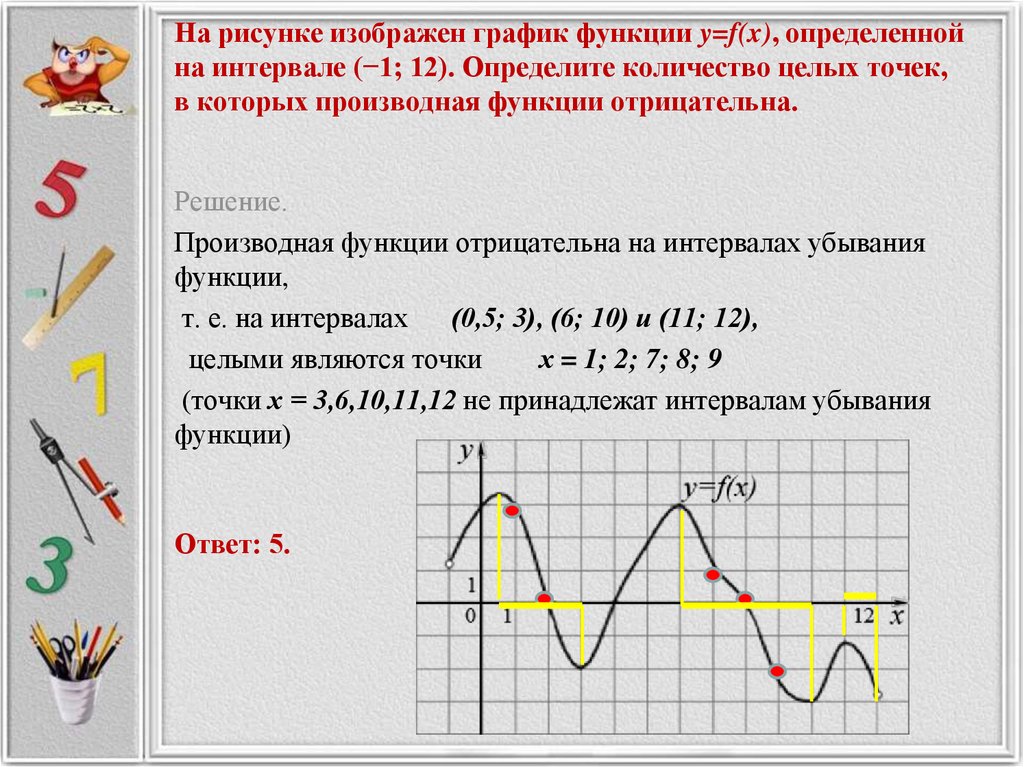
Использование производной для нахождения точек перегиба позволяет определить, где график функции изменяет свою кривизну.

Решаем все прототипы №12 из ЕГЭ по математике за 4 часа - Производная с нуля и до ЕГЭ
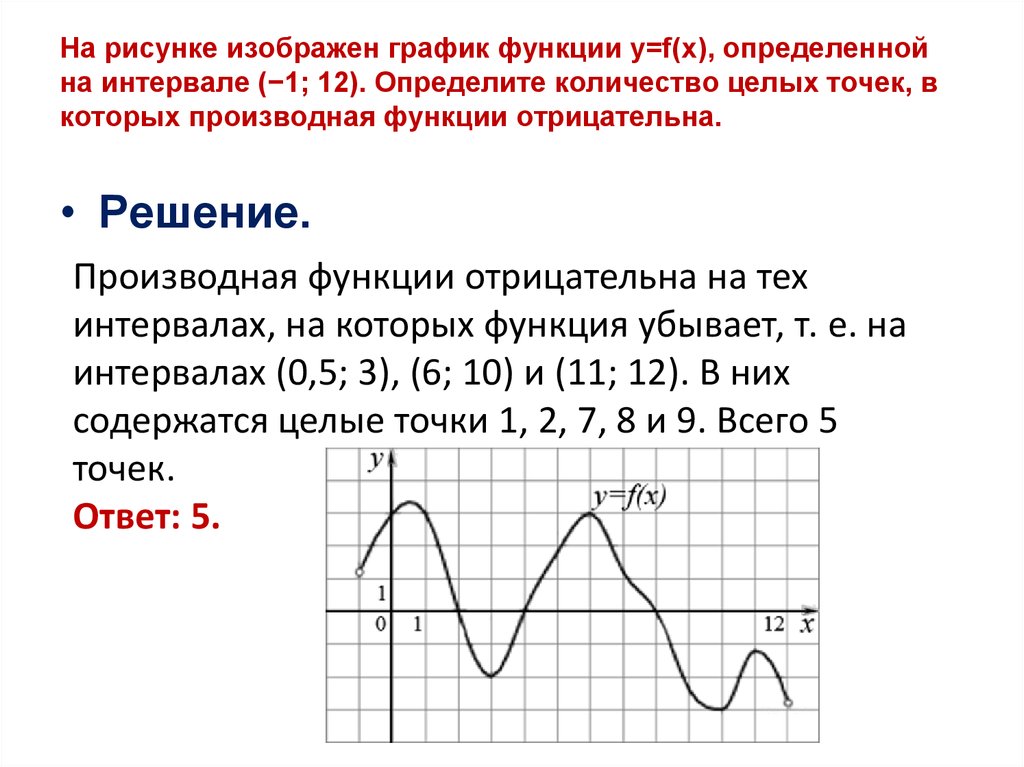
При анализе графика функции полезно учитывать, что если производная функции существует и непрерывна на интервале, функция будет гладкой и без разрывов.

Самый короткий тест на интеллект Задача Массачусетского профессора
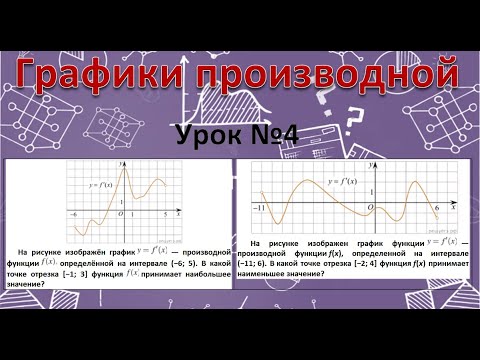
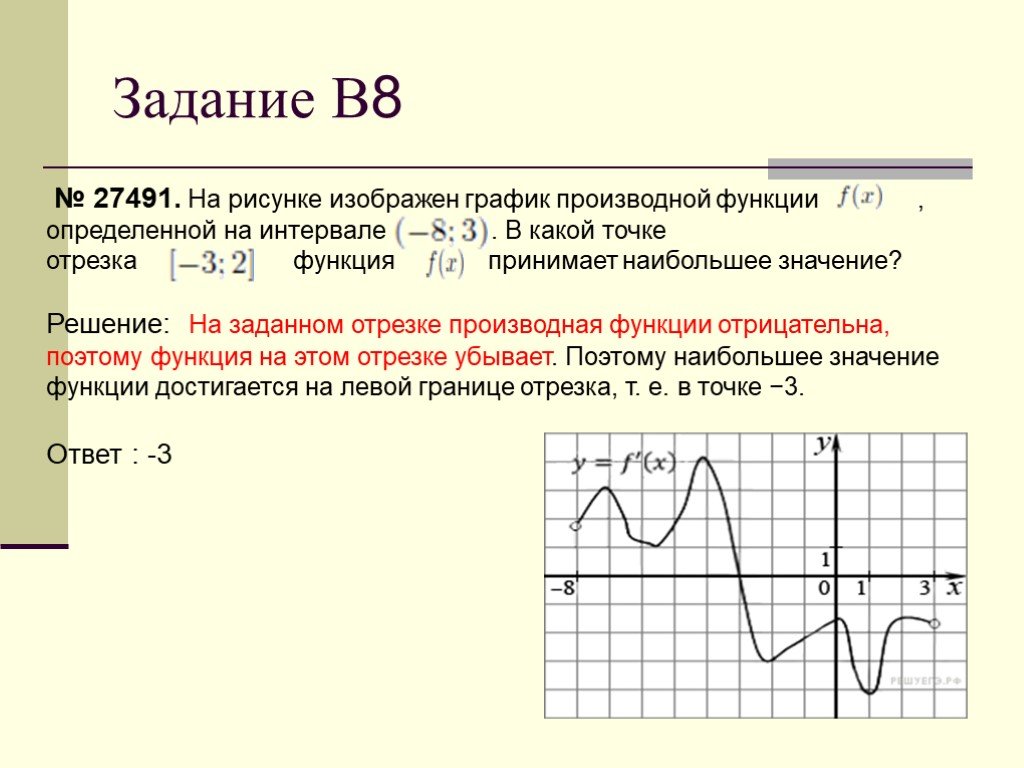
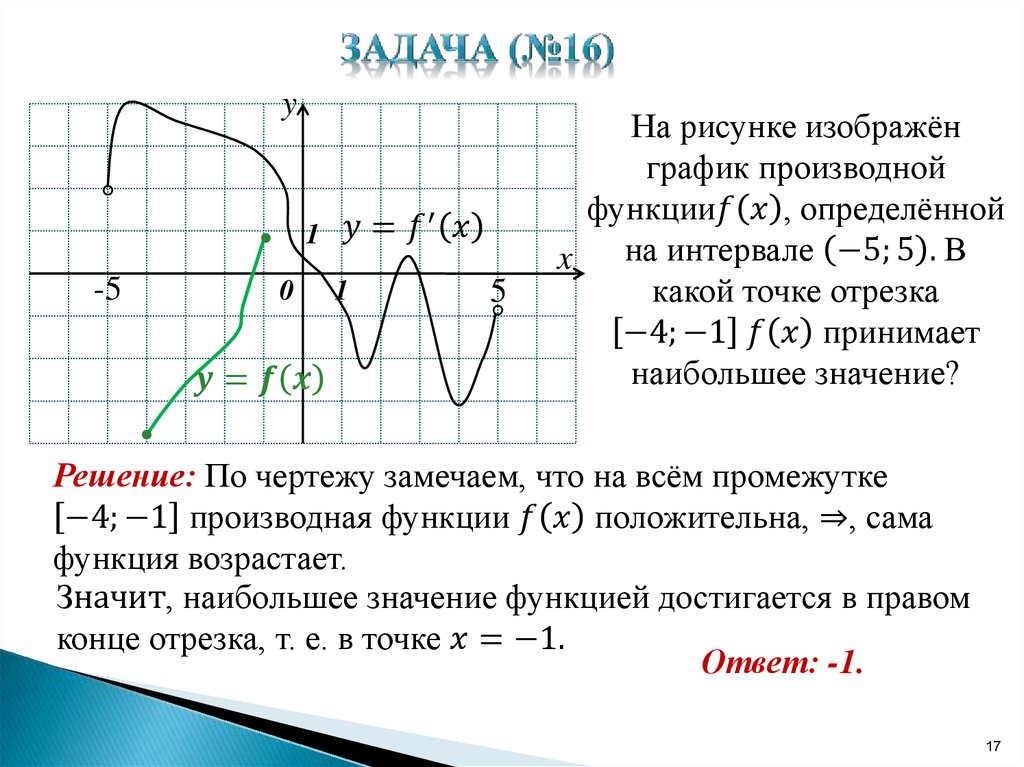
На рисунке изображён график —производной функции определённой на интервале . В какой точке отрезка
Для более точного анализа поведения функции можно использовать второй порядок производных, чтобы изучить, как изменяется сама скорость изменения функции.

Найти значение производной функции в точке. Алгебра 10 класс
При решении задач важно помнить, что производная не всегда существует в каждой точке: функции с разрывами или точками излома могут не иметь производной в этих точках.

4. Вычисление производных примеры. Самое начало.