Как правильно использовать формулы вписанных окружностей для успешного решения задач ЕГЭ по математике

На этой странице собраны полезные советы и ключевые формулы для решения задач с вписанными окружностями, которые могут встретиться на экзамене ЕГЭ по математике. Мы подробно разберем основные моменты, на которые стоит обратить внимание при подготовке, а также предложим практические рекомендации, которые помогут успешно справиться с заданиями на экзамене.

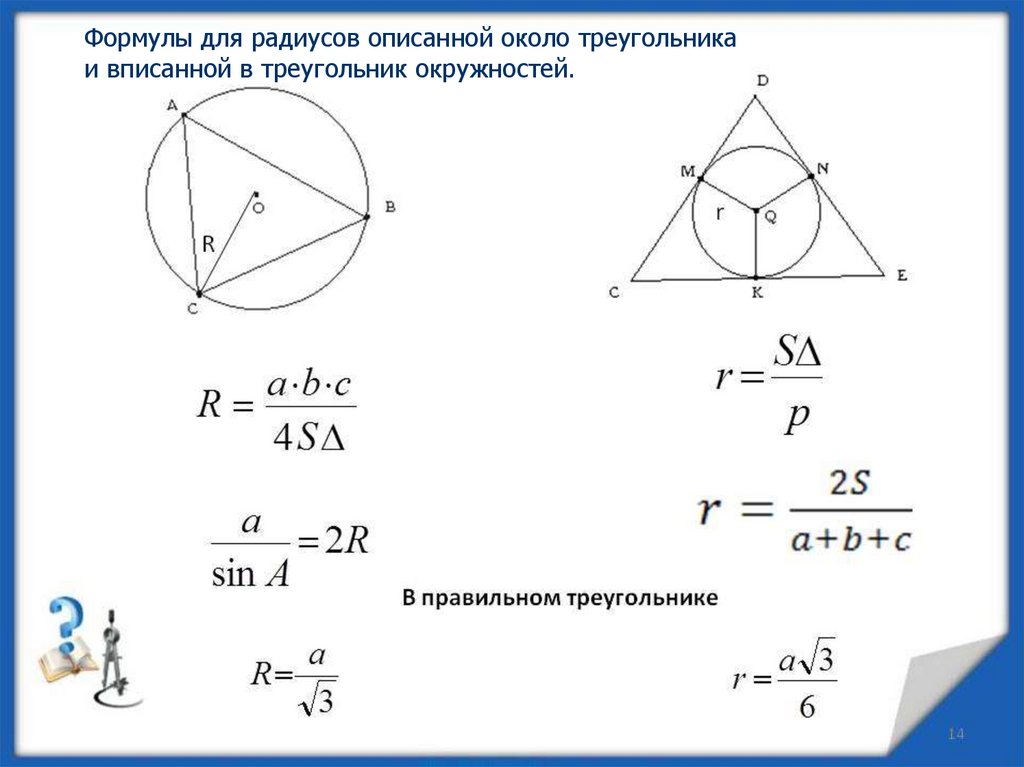
При решении задач на вписанные окружности важно помнить, что радиус окружности можно найти через площадь треугольника и его полупериметр.

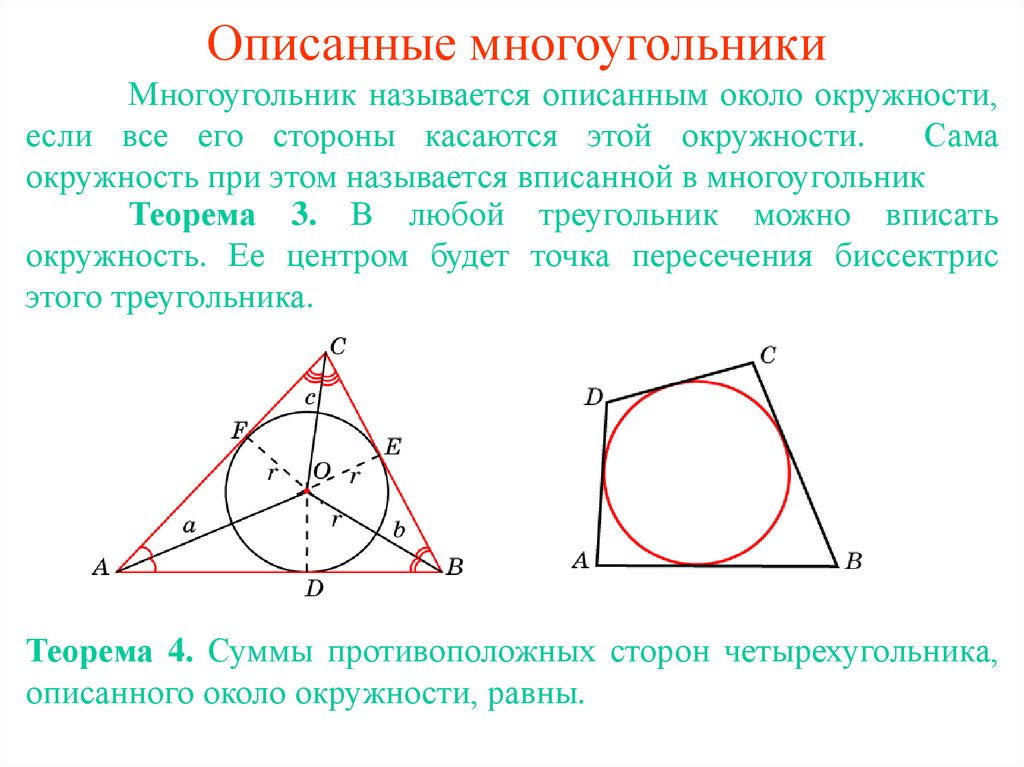
Не забывайте, что вписанная окружность касается всех сторон треугольника, а её центр — это точка пересечения его биссектрис.

Запомните формулу для радиуса вписанной окружности: r = S / p, где S — площадь треугольника, а p — его полупериметр.

Если в задаче дана информация о стороне треугольника и угле, можно воспользоваться теоремой о площади треугольника через сторону и угол для нахождения площади S.

Практикуйте нахождение полупериметра треугольника, так как это важная составляющая для применения формулы для радиуса вписанной окружности.

Не забывайте, что если треугольник является равнобедренным, то его биссектрисы и медианы совпадают, что облегчает нахождение центра вписанной окружности.

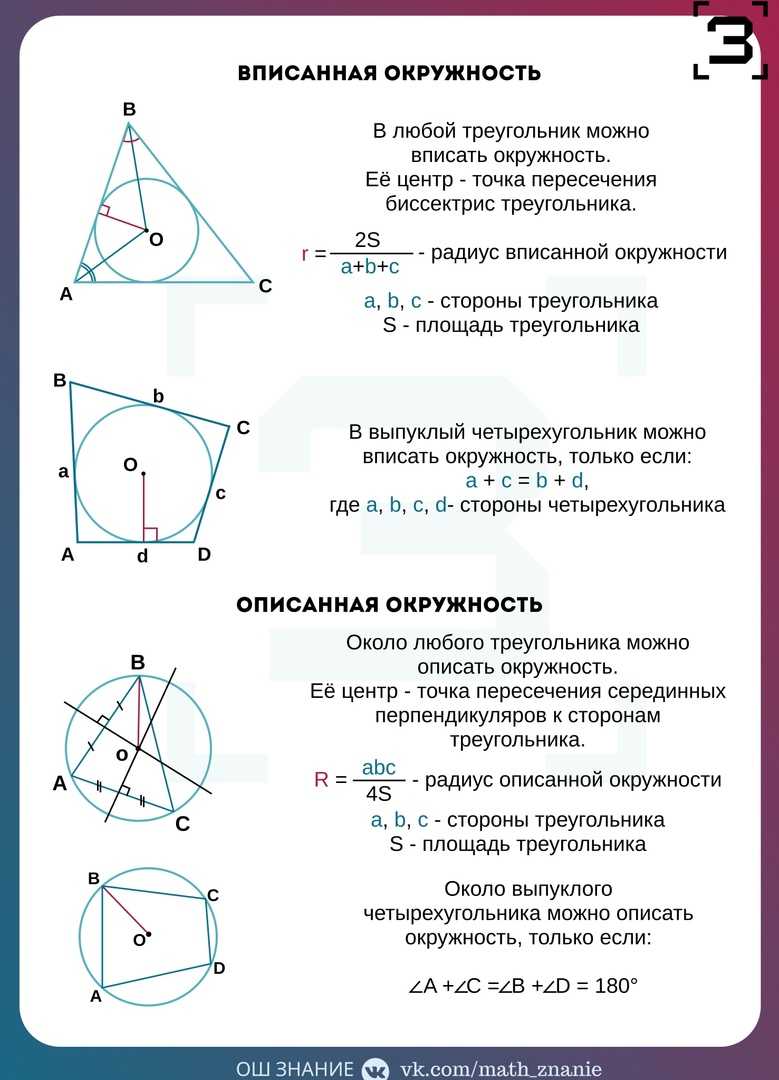
Для нахождения площади треугольника можно использовать различные методы, такие как формула Герона или через основание и высоту.

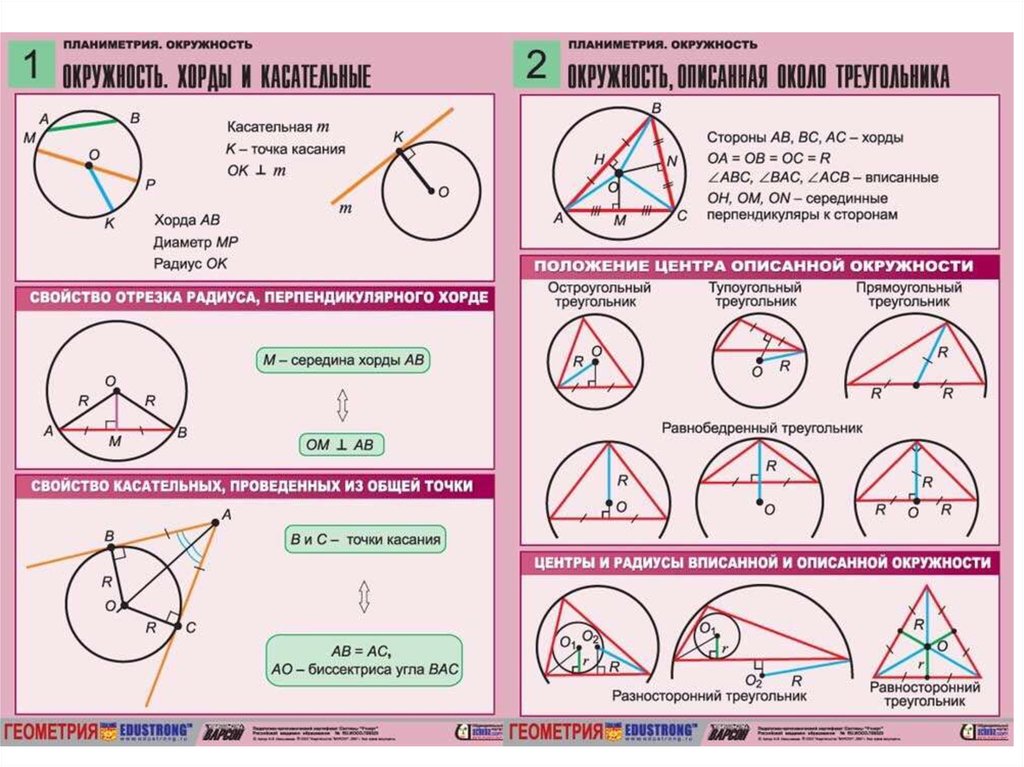
В задачах на вписанные окружности важно точно понимать, как использовать свойства касательных к окружности для нахождения длин сторон треугольника.

При решении задач с окружностями внимательно читайте условия задачи, чтобы не упустить важные геометрические связи и свойства треугольников.

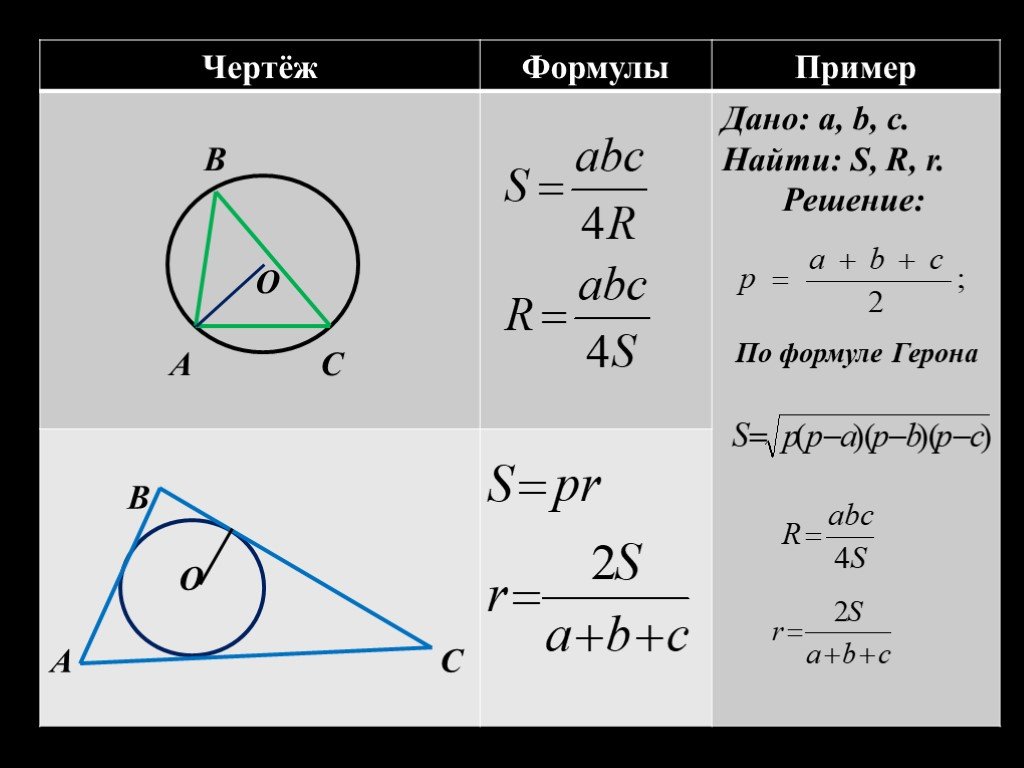
В задачах, где необходимо найти радиус вписанной окружности, всегда проверяйте все данные: иногда требуется применить дополнительные свойства треугольников или окружностей для точных расчетов.