Основы работы с векторами в базисе: ключевые моменты и полезные советы
Вектор в базисе векторов — важная концепция линейной алгебры, необходимая для эффективного решения многих математических задач. Правильное понимание этой темы позволяет упростить решение задач, связанных с преобразованиями векторных пространств, а также с вычислениями координат в различных базисах. В этой статье мы рассмотрим основные моменты, связанные с работой с векторами в базисе, а также предоставим практические советы для изучающих линейную алгебру.
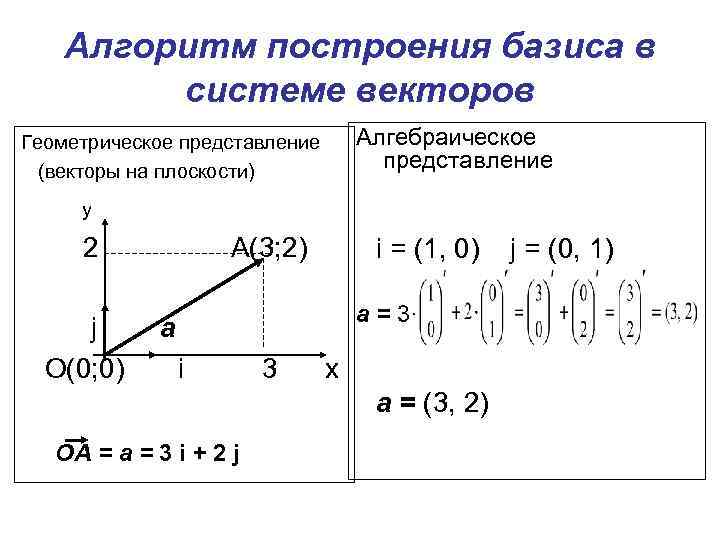


Для правильного понимания вектора в базисе, важно помнить, что базис задает систему координат, в которой любые векторы могут быть выражены через линейные комбинации его элементов.

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.


Всегда проверяйте, что векторы вашего базиса линейно независимы, иначе базис будет неполным и не сможет адекватно описать все пространство.

Как разложить вектор по базису - bezbotvy

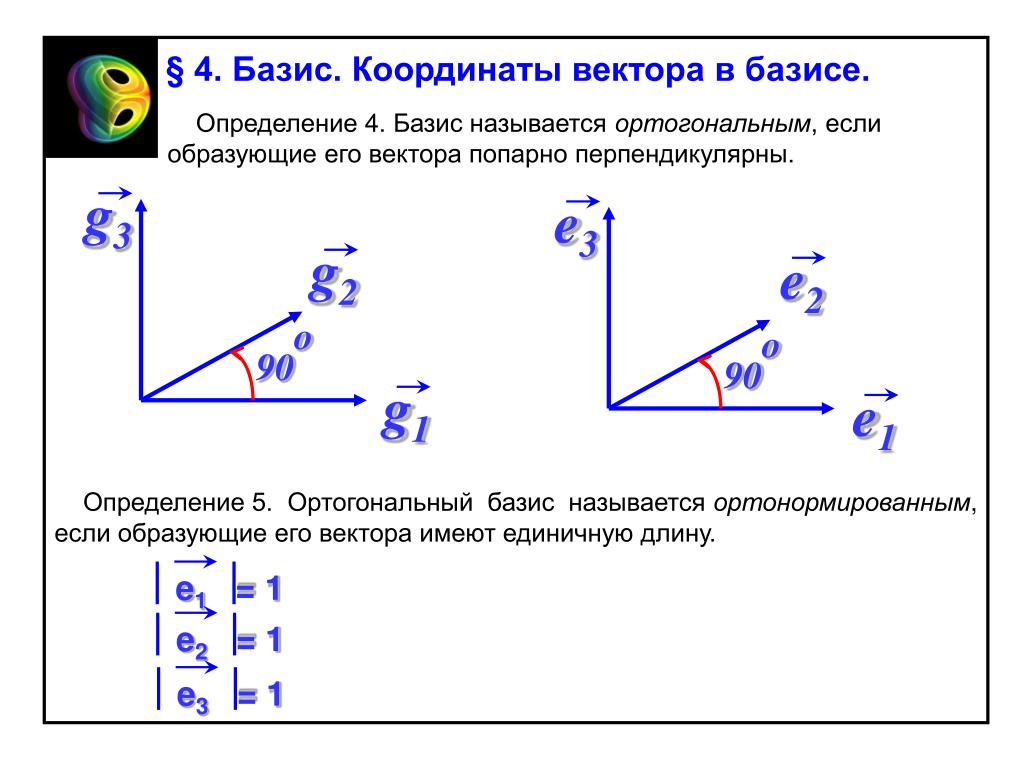
Для вычислений координат вектора в новом базисе используйте матрицу перехода между базисами — это упростит вычисления и позволит избежать ошибок.

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисе

При работе с векторами в базисе важно уметь преобразовывать координаты между различными базисами, что требует знания матриц перехода и их свойств.

Высшая математика. Линейные пространства. Векторы. Базис
Убедитесь, что понимаете разницу между каноническим базисом и произвольным базисом, так как это влияет на выбор методов решения задач.
Линейные комбинации, span и базисные вектора - Сущность Линейной Алгебры, глава 2

Практикуйтесь в нахождении координат вектора в различных базисах, это поможет вам быстрее ориентироваться в заданиях на экзаменах.

Найдите разложение вектора по векторам (базису)

Для упрощения задач по векторным пространствам полезно использовать геометрическое представление векторов, чтобы визуализировать их связь с базисом.
Не забывайте, что преобразования вектора в новый базис часто требуются при решении задач на линейные преобразования или при работе с системой линейных уравнений.
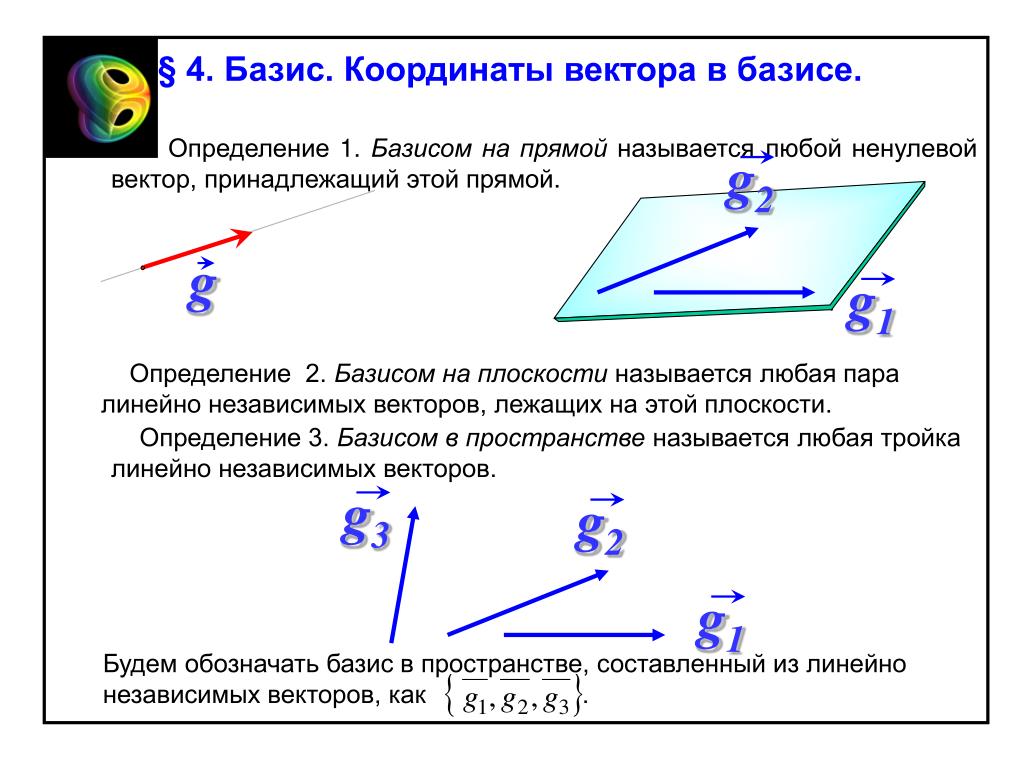

Решение задач на преобразование векторов в новые базисы требует четкого понимания алгоритмов умножения матриц и обращения матриц.

Разложение вектора по базису. 9 класс.

Используйте базис для упрощения сложных выражений, например, при вычислениях с матрицами или при решении систем линейных уравнений.
