Методы вычисления вектора нормали прямой из канонического уравнения: практические рекомендации
На этой странице представлены полезные советы и методы для нахождения вектора нормали прямой из канонического уравнения. Узнайте, как правильно применить математические формулы и избежать ошибок в расчетах.
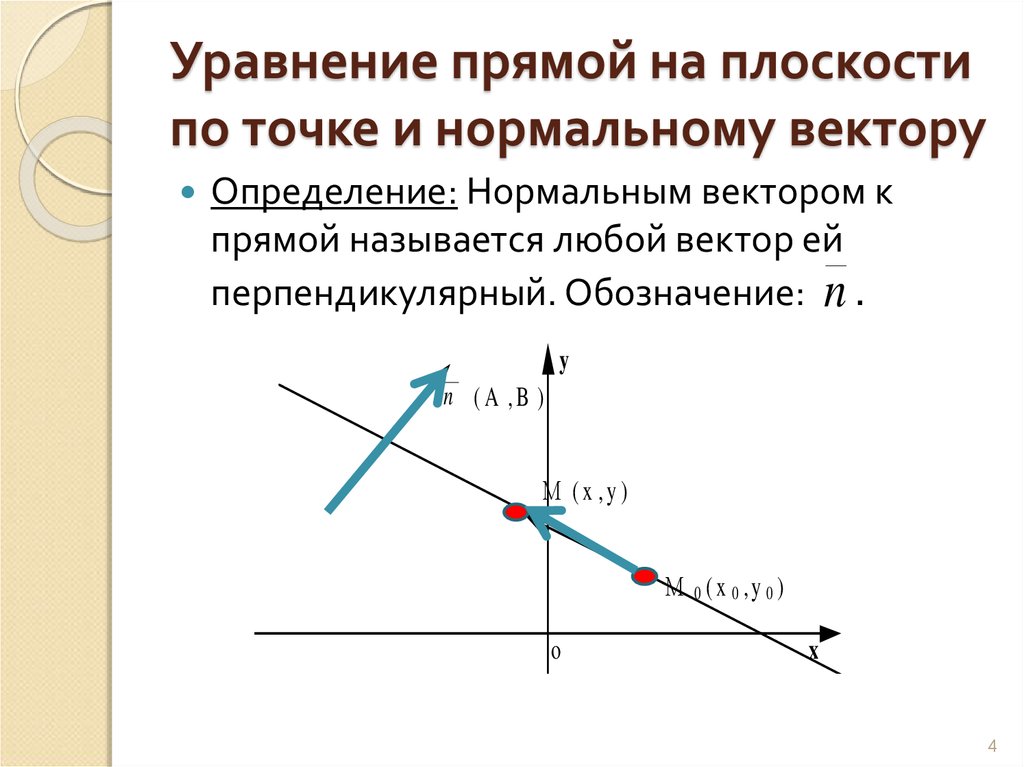

Чтобы найти вектор нормали прямой, достаточно взять коэффициенты при x и y из канонического уравнения прямой.
Уравнения прямой на плоскости - Векторная алгебра


Вектор нормали всегда перпендикулярен самой прямой, поэтому его направление можно определить по коэффициентам канонического уравнения.

Лекция 23. Виды уравнений прямой на плоскости.

Важно помнить, что вектор нормали не зависит от константы в уравнении прямой, он определяется только коэффициентами при x и y.

Геометрия. 9 класс. Уравнение прямой. Направляющий вектор и вектор нормали прямой /22.10.2020/


Если у вас есть каноническое уравнение вида Ax + By + C = 0, то вектор нормали будет равен (A, B).
Направляющий и нормальный вектор прямой на плоскости - Векторная алгебра
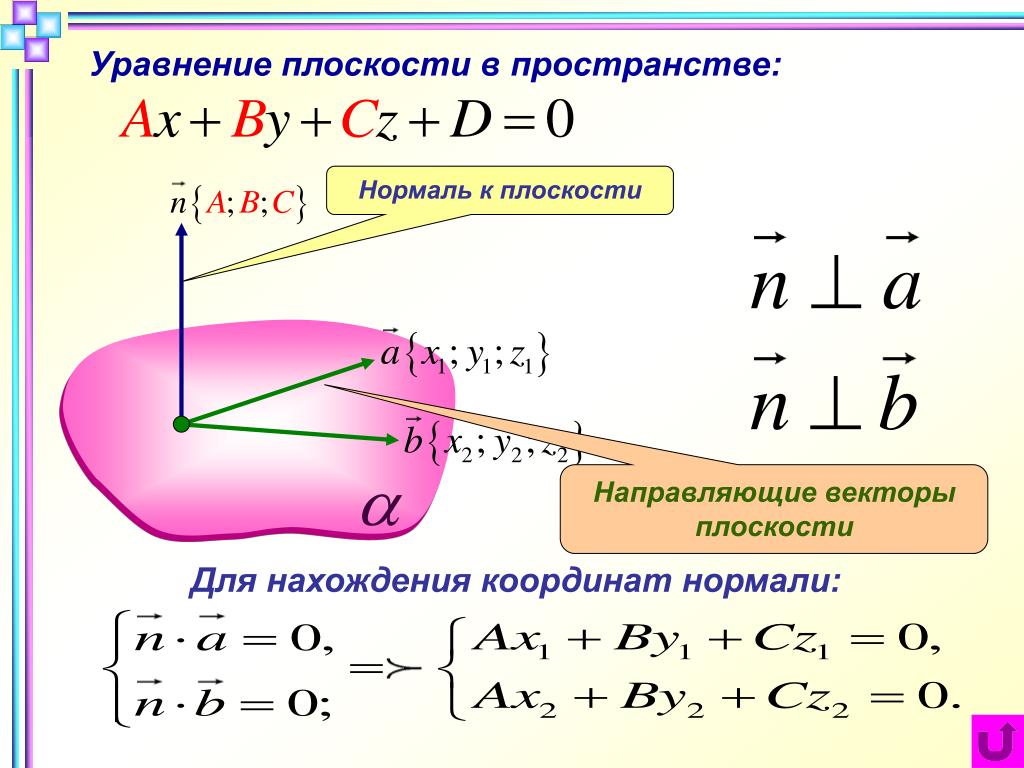
Для точности расчетов, всегда приводите уравнение прямой к каноническому виду перед нахождением вектора нормали.

Написать канонические и параметрические уравнения прямой в пространстве

При работе с каноническим уравнением прямой важно обратить внимание на знаки коэффициентов: положительные и отрицательные значения могут влиять на направление нормали.

Для получения единичного вектора нормали, можно нормировать вектор (A, B), деля его на длину.
Для решения задач на нахождение вектора нормали рекомендуется практиковаться на примерах с разными уравнениями прямых, чтобы лучше понимать закономерности.

Видеоурок \
Если уравнение прямой задано в другом виде, например, в общем виде Ax + By + C = 0, его можно преобразовать в каноническое, разделив обе части на коэффициент A или B.
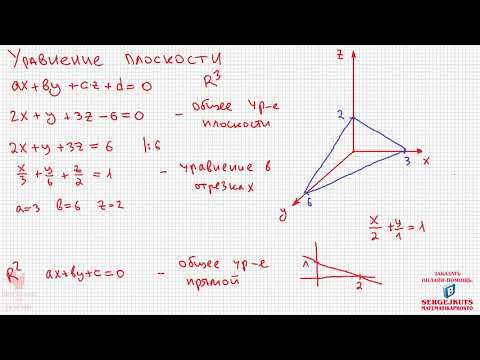
Математика без Ху%!ни. Уравнение плоскости.

Не забывайте, что вектор нормали может быть выражен в любом масштабе, главное — правильно соблюдать его ориентацию относительно прямой.

Математика без Ху%!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.
