Основные методы и рекомендации для работы с уравнениями парабол, гипербол и прямых
На этой странице вы найдете полезные советы и примеры для работы с уравнениями парабол, гипербол и прямых. Мы подробно рассмотрим, как решать различные задачи, связанные с этими кривыми, и поделимся рекомендациями по быстрому нахождению решений. Уравнения этих фигур играют важную роль в аналитической геометрии, и умение работать с ними обязательно пригодится при решении математических задач.
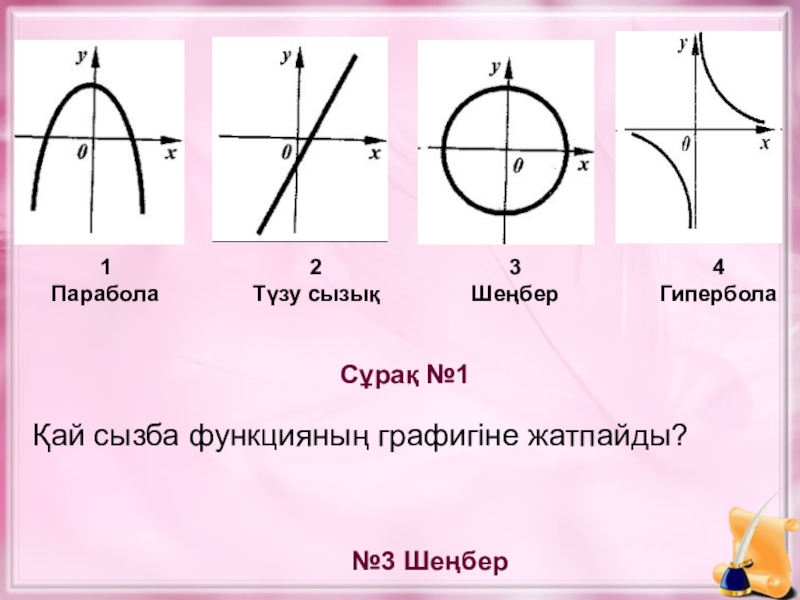

При решении уравнений параболы важно правильно выбрать фокус и директрису, так как они напрямую определяют форму и направление кривой.
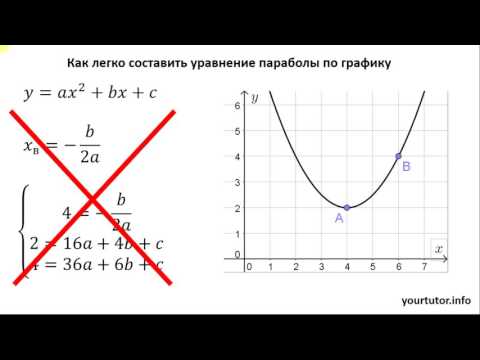
Как легко составить уравнение параболы из графика
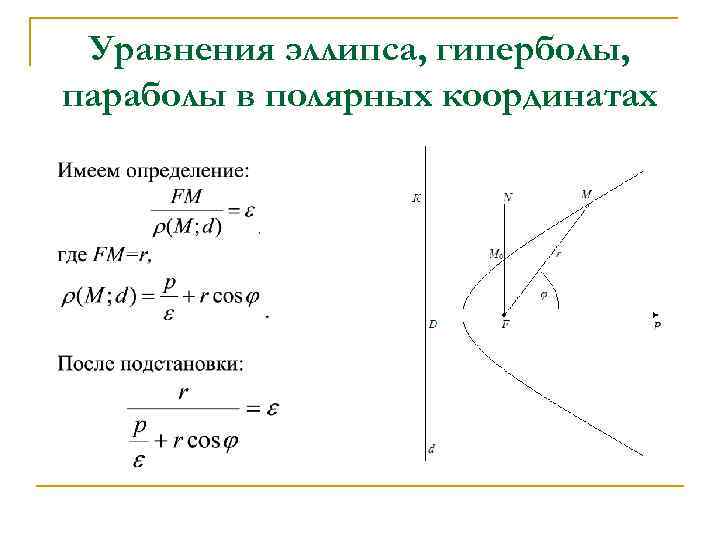
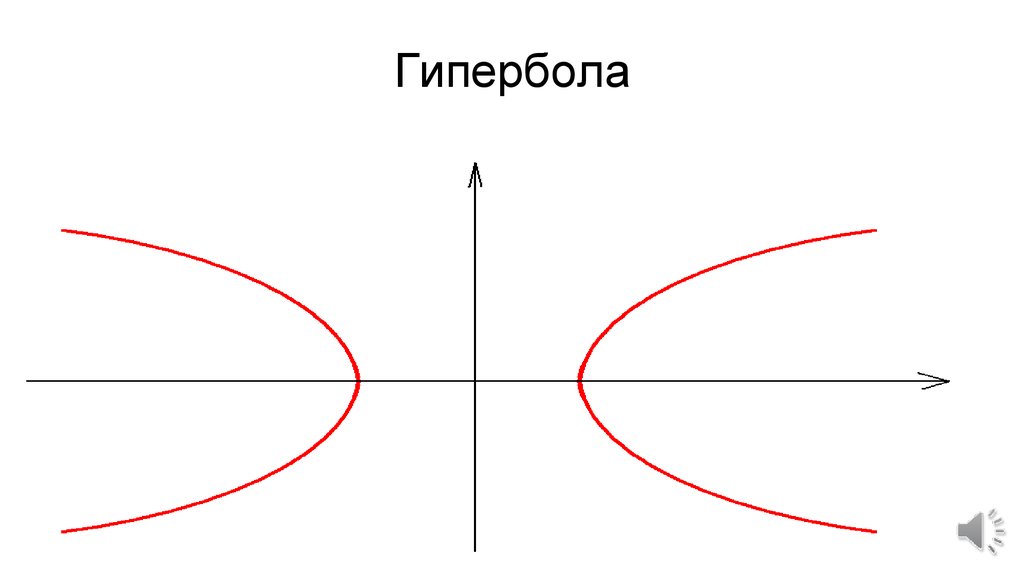
Для гиперболы убедитесь, что правильно определены ее асимптоты, так как они определяют поведение графика на больших расстояниях.

ПАРАБОЛЫ И ГИПЕРБОЛЫ НА ИЗИ
Когда решаете уравнение прямой, всегда проверяйте, что у вас правильно указаны координаты точек, через которые проходит прямая.

Математика ОГЭ Пересечение двух графиков прямой и параболы
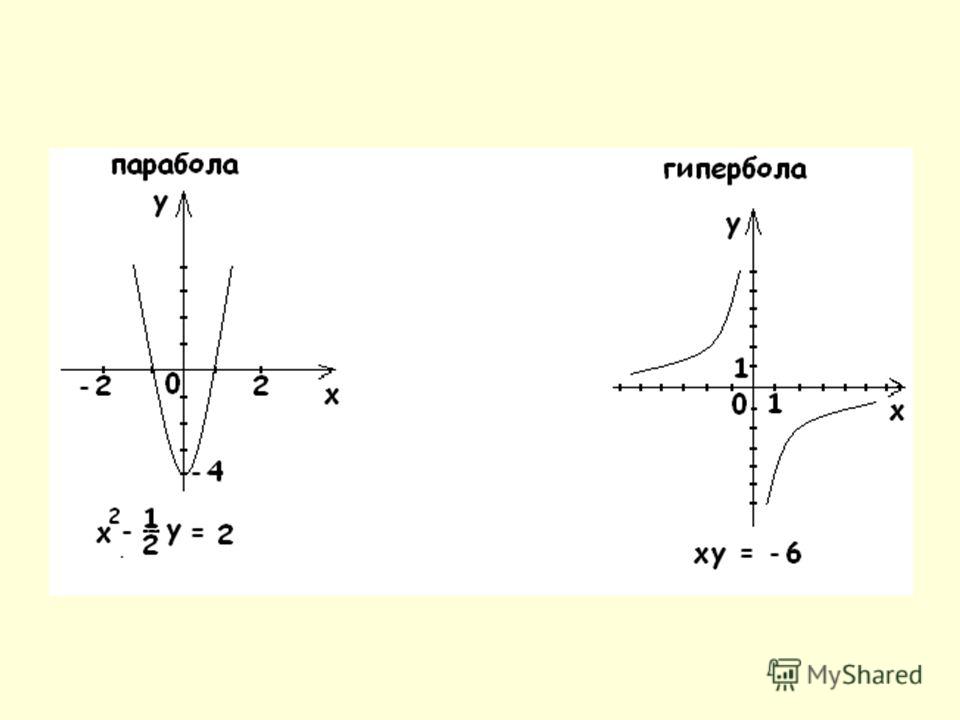
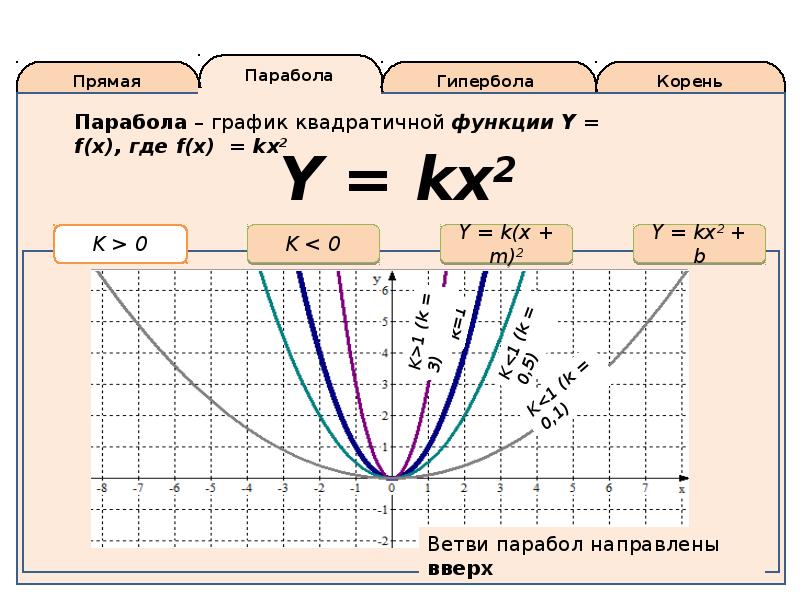
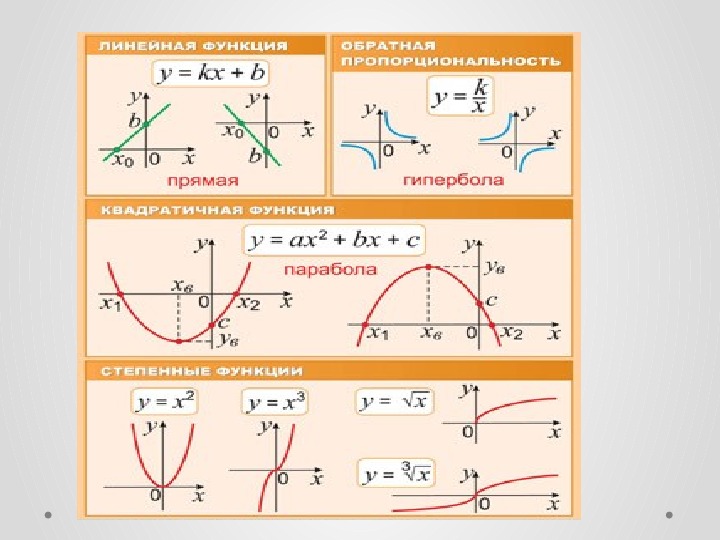
При анализе параболы используйте стандартные формы уравнений (например, y = ax^2 + bx + c), чтобы быстрее находить ключевые характеристики кривой.
Гипербола, прямая и полуплоскость - Параметр 78 - likerkacinema.ru #егэ2024
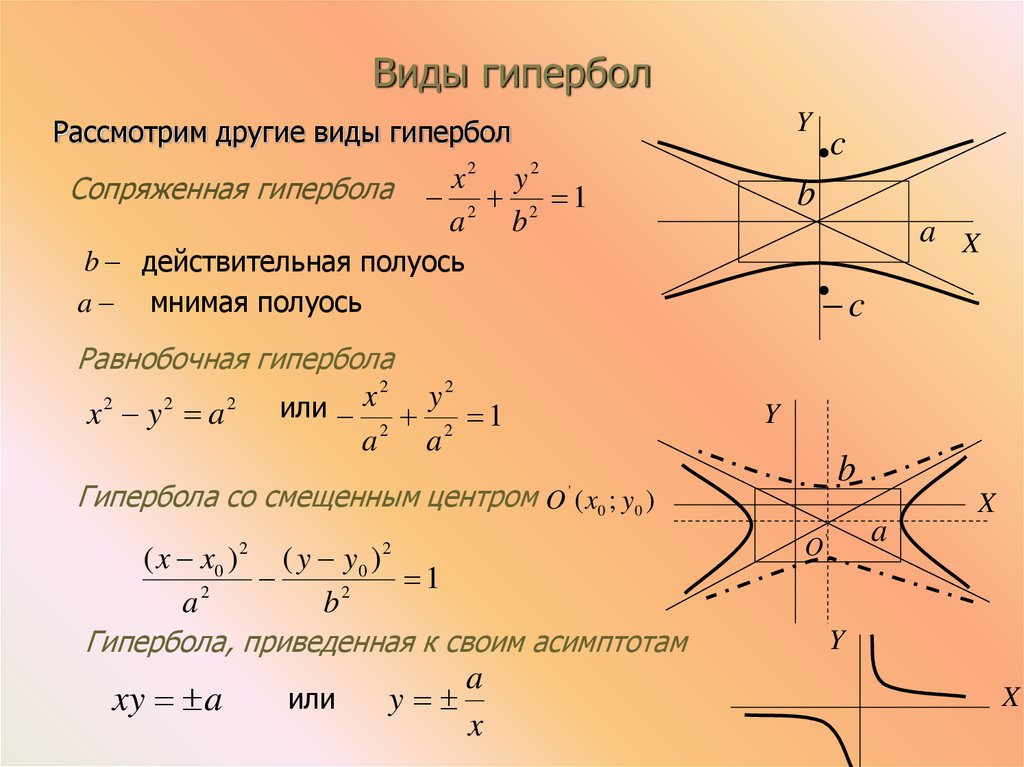

Для гиперболы полезно понять, как меняются координаты фокусов в зависимости от ориентации гиперболы, это упростит решение задач.

Всё о квадратичной функции. Парабола - Математика TutorOnline

При построении графиков прямых и кривых используйте систему координат с четкими делениями для точности построений.
Если уравнение прямой имеет вид Ax + By + C = 0, можно выразить ее в виде y = mx + b для удобства построения графика.

Графики функций-Парабола, прямая и гипербола
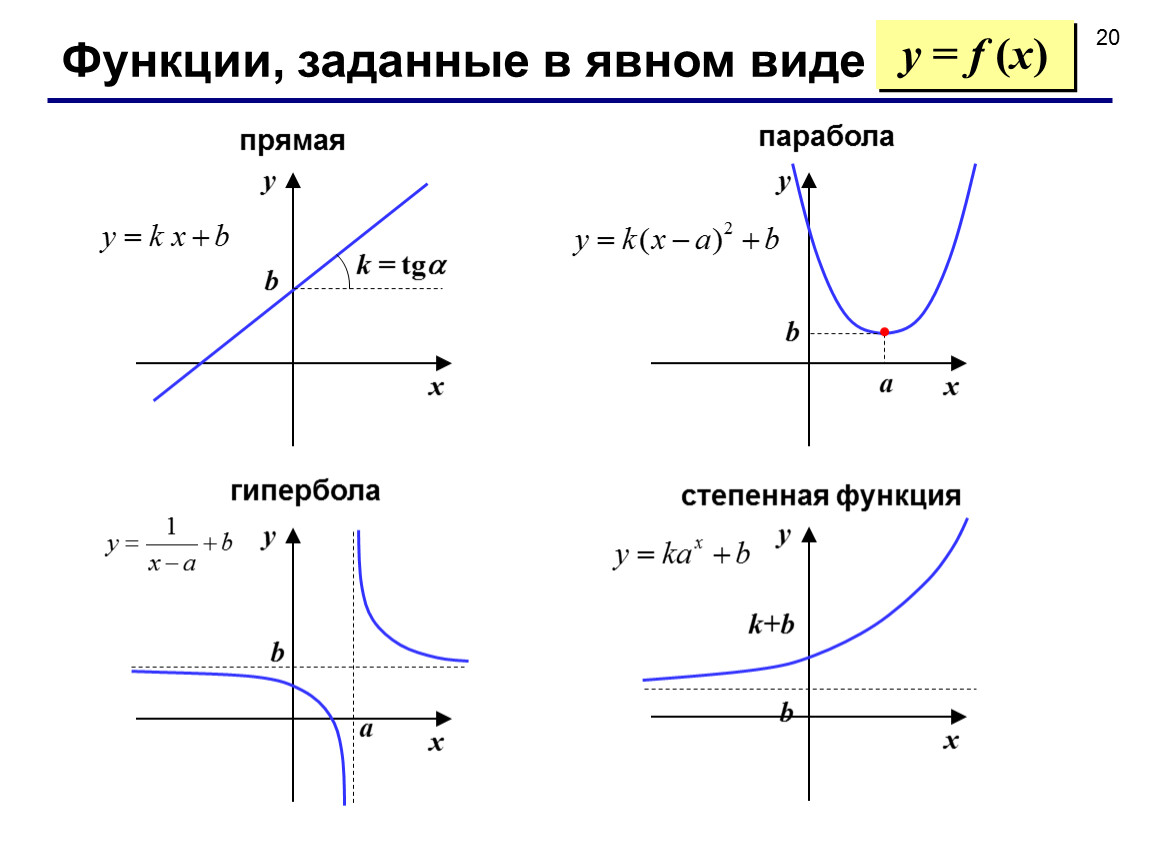
Не забывайте про симметрию параболы относительно оси, это поможет вам найти дополнительные точки на графике без вычислений.

Сопоставление графиков параболы и гиперболы в ОГЭ по математике

11-2 задание ОГЭ по математике - ГРАФИКИ - Прямая, парабола, гипербола
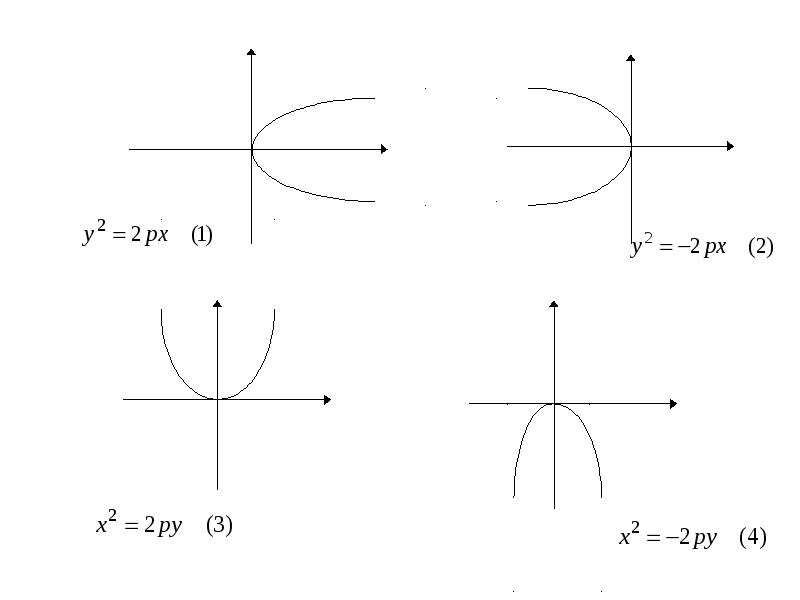
Используйте метод замены переменных для упрощения уравнений гиперболы, особенно когда они представлены в сложной форме.
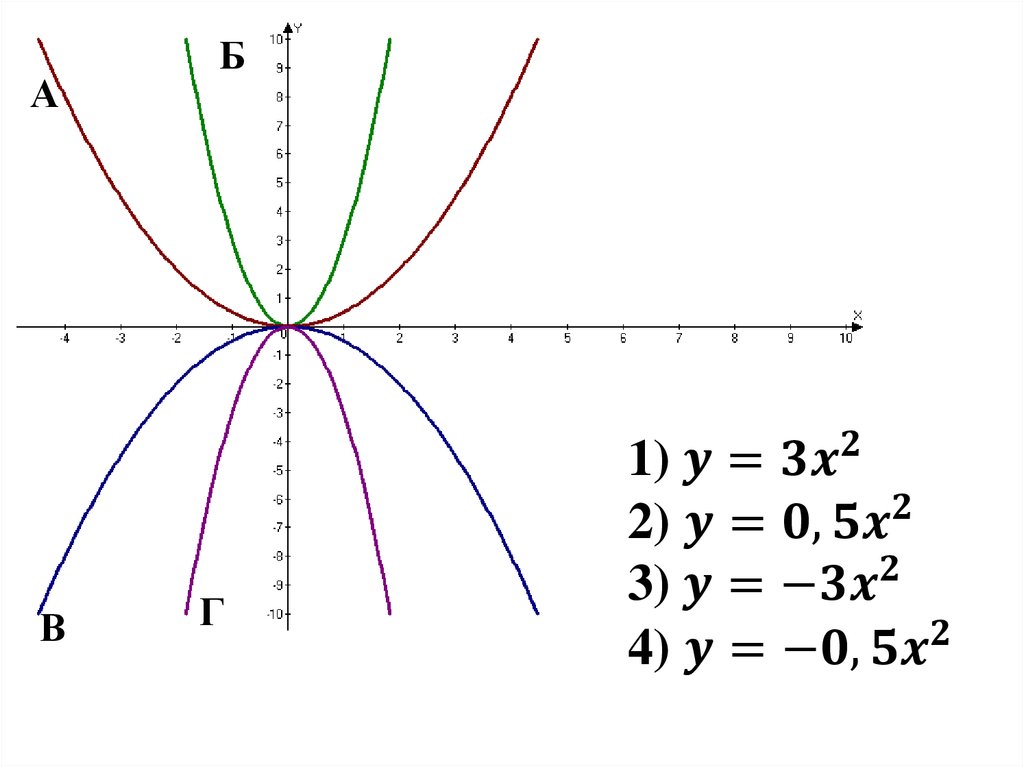
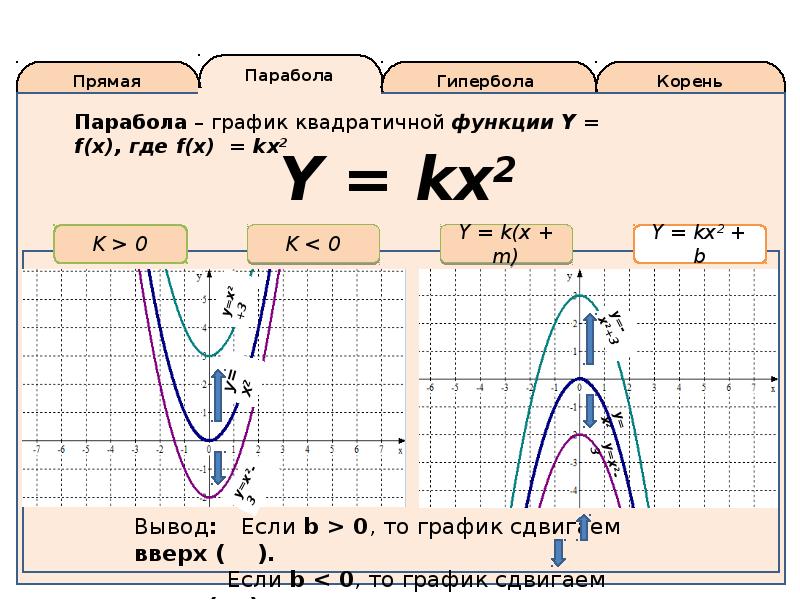
При решении задач с параболами и гиперболами полезно изучить их свойства через производные, чтобы лучше понять поведение кривых на различных участках.
