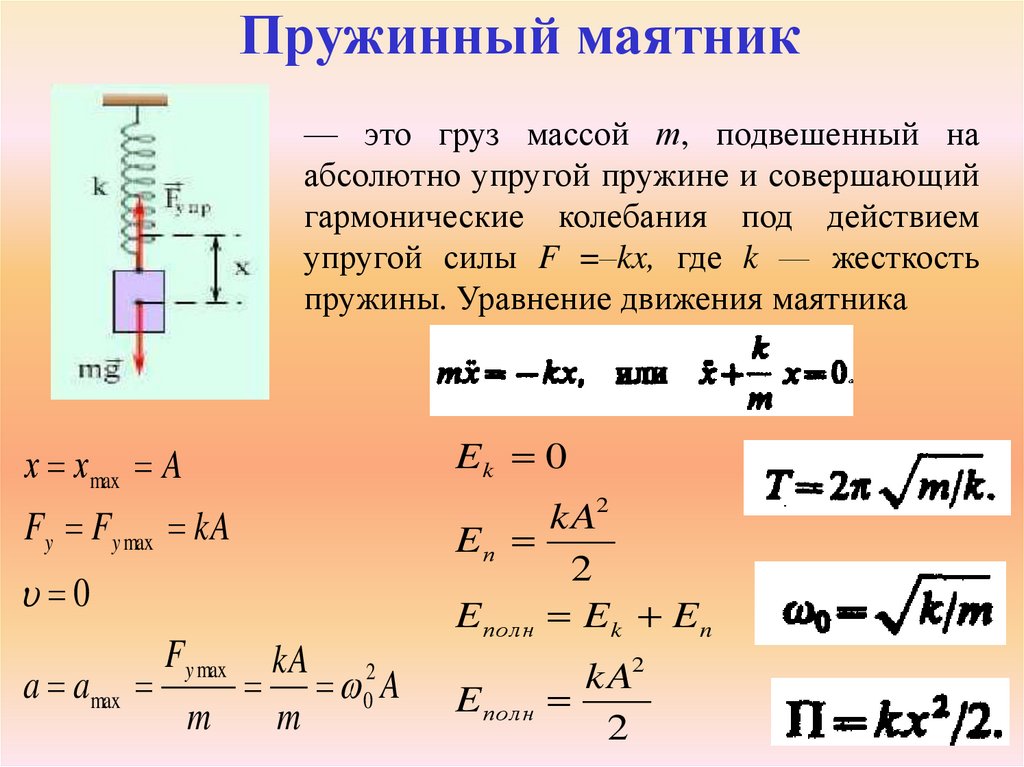
Основные аспекты уравнения движения пружинного маятника и его формулы
Пружинный маятник — классический пример гармонических колебаний, часто используемый для демонстрации основных законов механики. Для описания его движения применяется специальное уравнение, которое учитывает массу, жесткость пружины и амплитуду колебаний. В этой статье мы рассмотрим ключевые моменты в расчете и применении формул для определения характеристик свободных колебаний пружинного маятника.

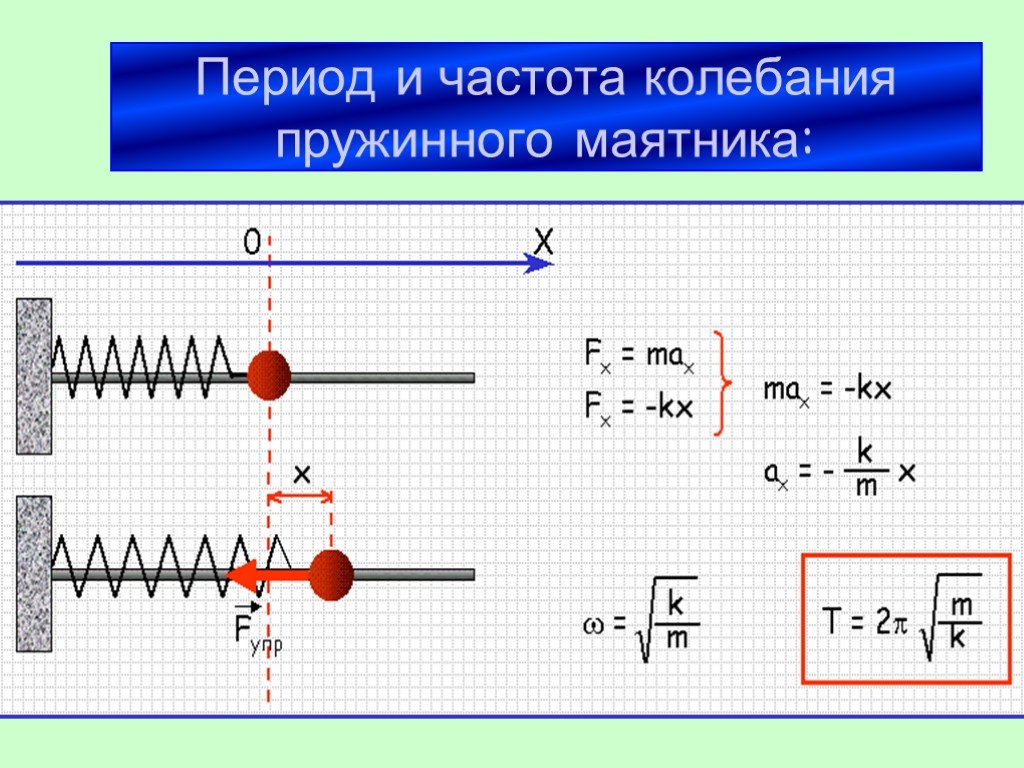

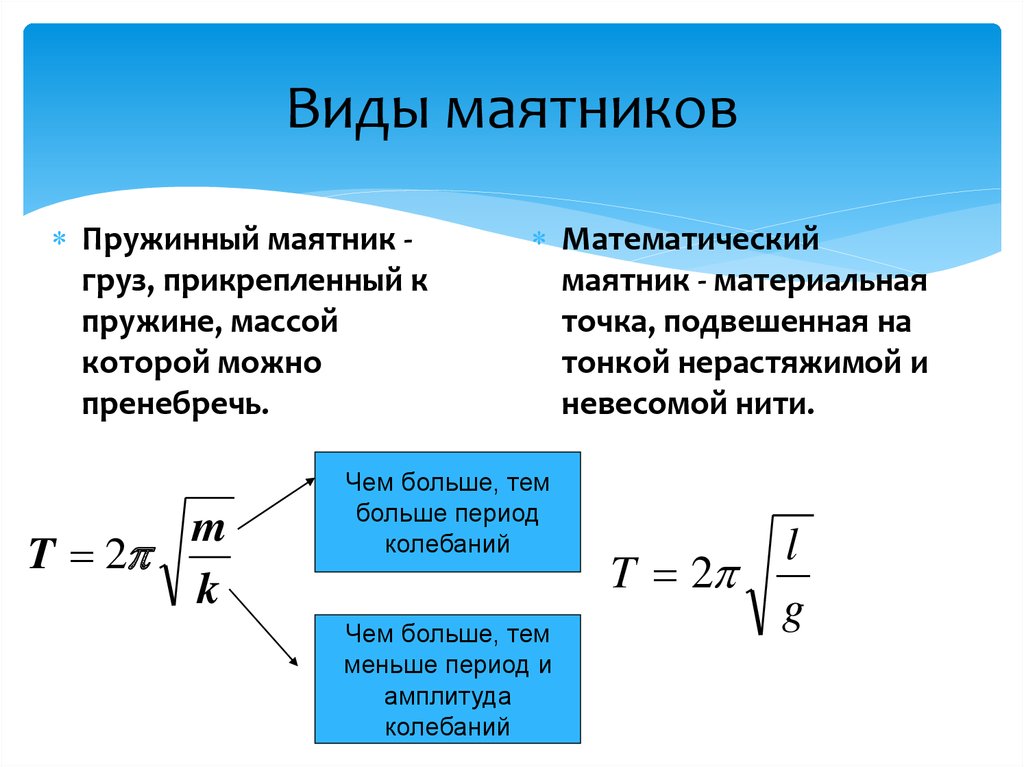
Не забывайте, что для определения периода колебаний пружинного маятника важен не только коэффициент жесткости пружины, но и масса тела, которое подвешено на пружине.

Механические колебания. Как найти период колебаний? - ЕГЭ 2023 по физике


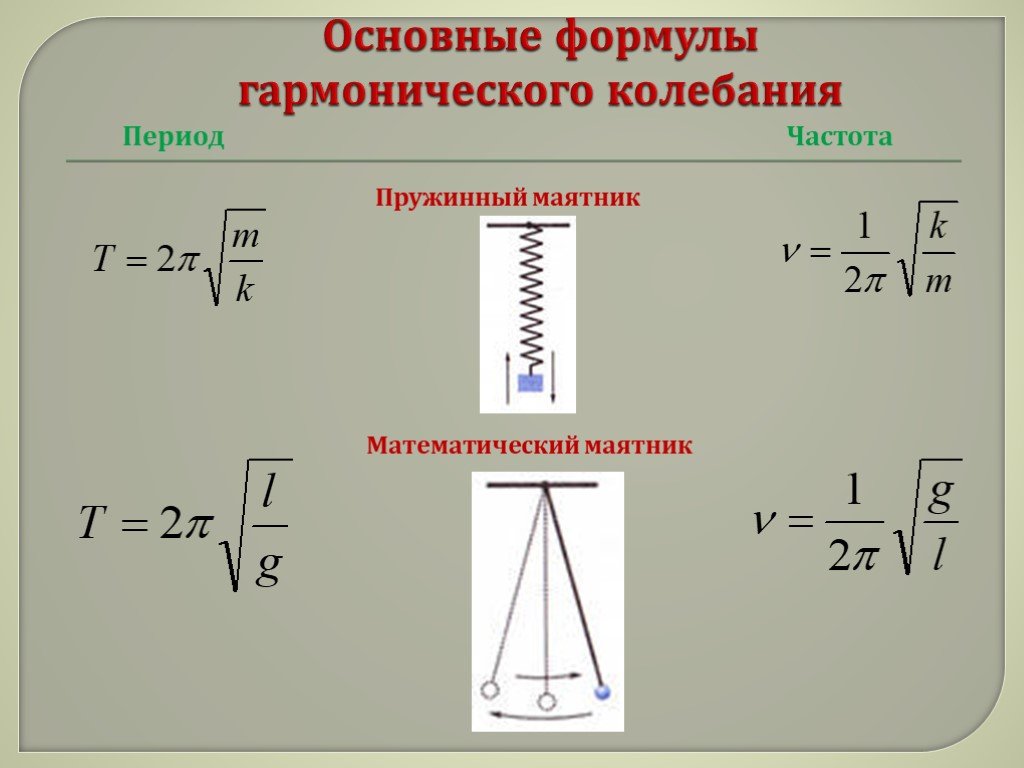
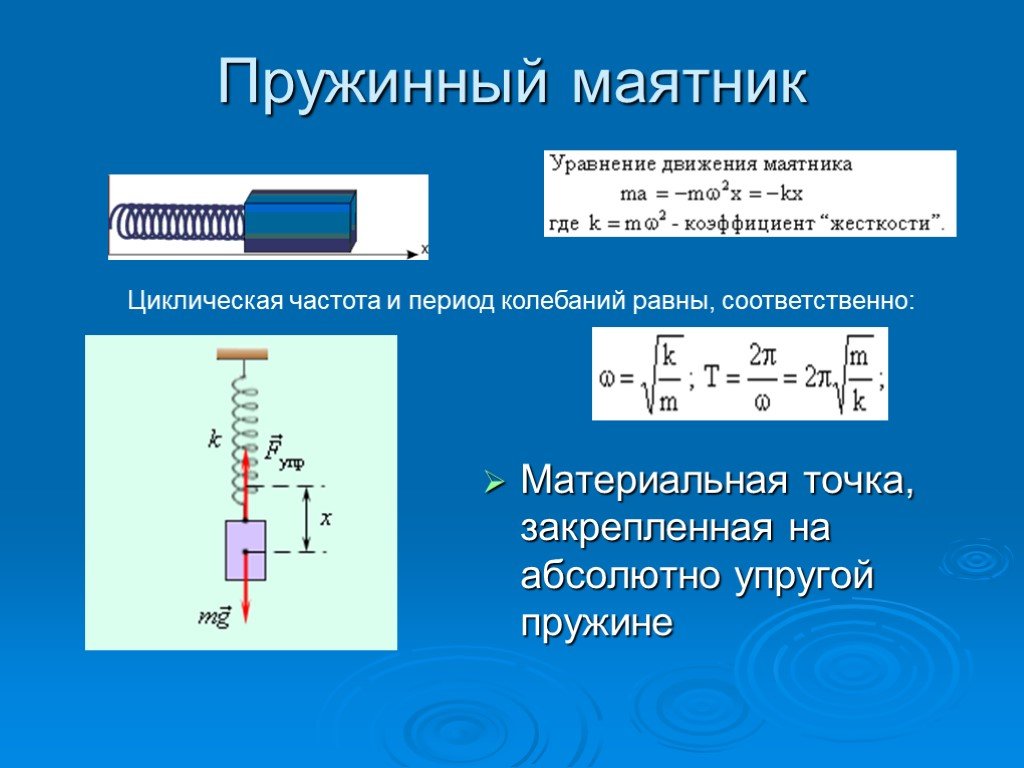
Уравнение свободных колебаний пружинного маятника имеет вид: m * d²x/dt² + k * x = 0, где m — масса тела, k — жесткость пружины, x — смещение от положения равновесия.

Колебания математического и пружинного маятников. 9 класс.
Для того чтобы точно рассчитать период колебаний маятника, используйте формулу T = 2π√(m/k), где T — период колебаний, m — масса тела, а k — жесткость пружины.

Период математического и пружинного маятни
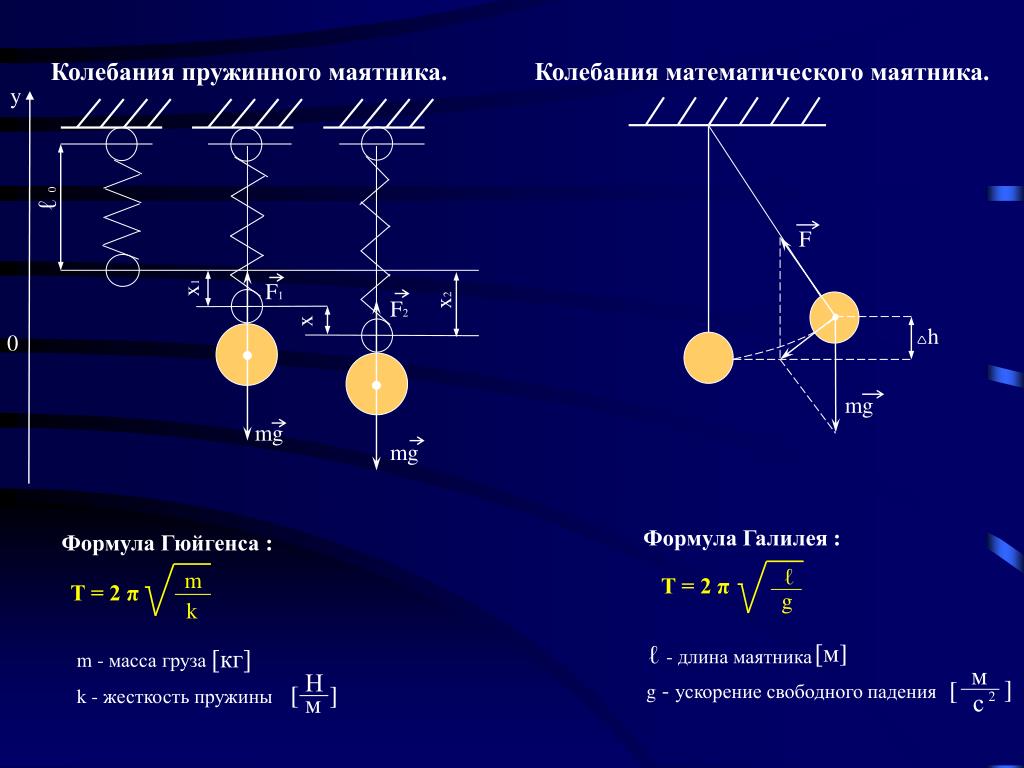

Прежде чем применять формулы, убедитесь, что ваша система не подвергается внешним воздействиям (например, сопротивлению воздуха или трению), так как это может существенно изменить результаты расчетов.

Лабораторная пружинный маятник

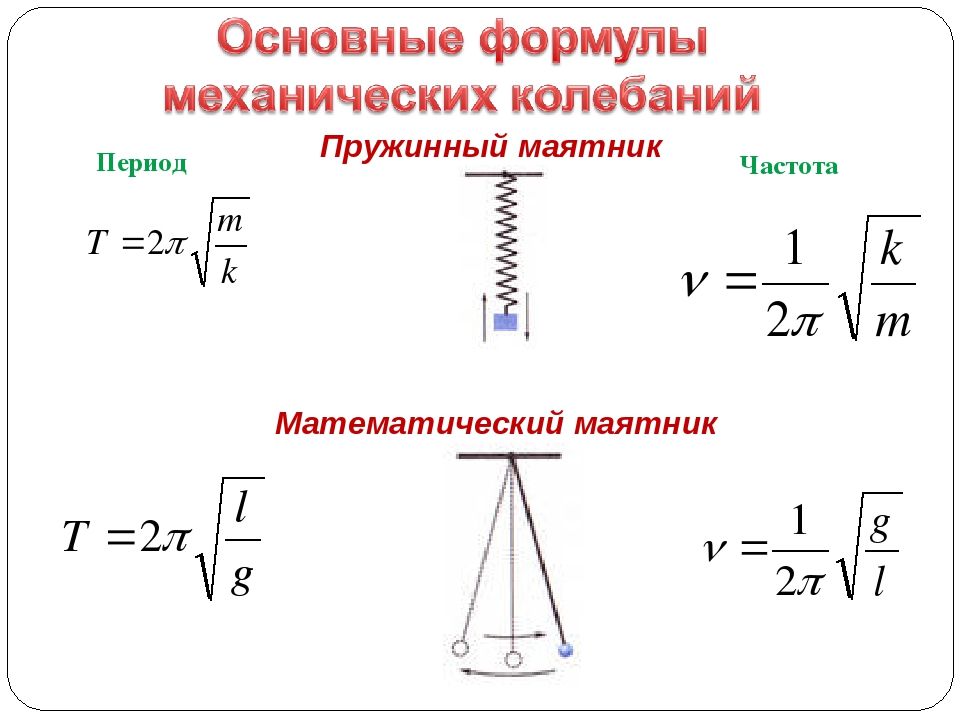
Важно учитывать, что амплитуда колебаний не влияет на период пружинного маятника в идеальных условиях — колебания остаются изотропными.

Горизонтальный пружинный маятник

Если вам нужно учитывать неидеальные условия, например, потерю энергии на трение, добавьте в уравнение дифференциальную составляющую для сопротивления среды.

Самый короткий тест на интеллект Задача Массачусетского профессора
Для более точных расчетов можно использовать численные методы, такие как метод Эйлера или Рунге-Кутты, если решение уравнений движения не получается аналитически.

Математические и пружинные маятники. 11 класс.
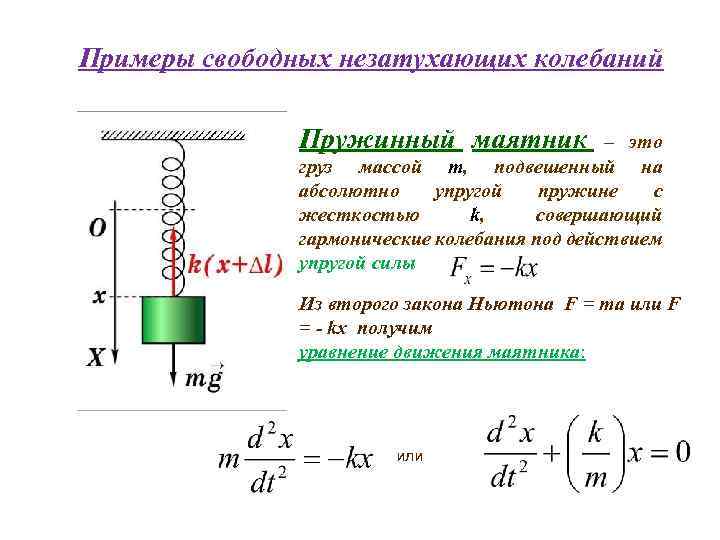
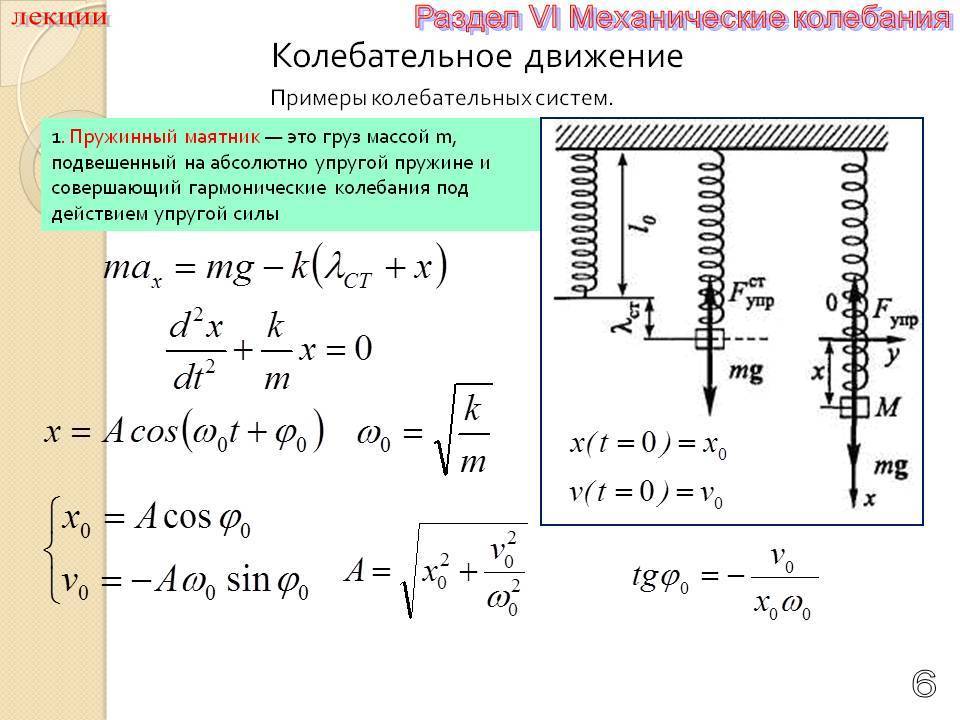
Для проверки правильности расчетов сделайте эксперимент: подвесьте тело на пружине, измерьте амплитуду и период колебаний, затем сравните полученные данные с теоретическими расчетами.


Помимо теоретических расчетов, изучите визуализацию колебаний — это поможет лучше понять динамику системы и применить формулы на практике.

Не забывайте, что на реальных маятниках могут быть дополнительные факторы, влияющие на движение, такие как деформация пружины или изменение температуры, что также важно учитывать при расчетах.

Видеоурок по физике \