Советы по упрощению выражений с дробями и степенями в математике
В этой подборке собраны полезные советы и методы, которые помогут вам упростить выражения с дробями и степенями. Разберемся, как правильно работать с такими выражениями и ускорить решение математических задач.



Всегда проверяйте, можно ли сократить дробь перед выполнением других операций.

Действия с алгебраическими дробями - Математика - TutorOnline


Помните, что степень степени умножается: (a^m)^n = a^(m*n).

Алгебра ВСЕ Темы за 8 Класс / Математика с НУЛЯ за 30 МИНУТ / Маркова

Используйте свойства степени с основанием 1, так как 1 в любой степени всегда остается равным 1.

Задание №1 \

Если дробь имеет одинаковые множители в числителе и знаменателе, их можно сократить.

8 класс, 4 урок, Преобразование алгебраических выражений

При работе с дробями старайтесь всегда привести их к общему знаменателю перед сложением или вычитанием.
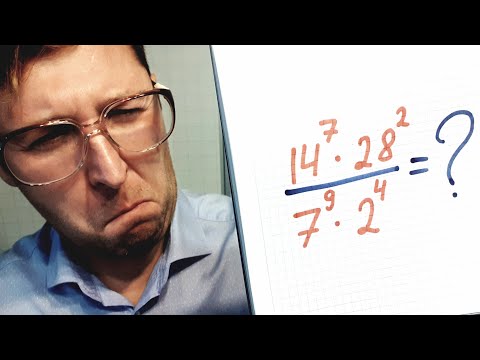
Сокращаем дроби со степенями №2. Алгебра 8 класс.
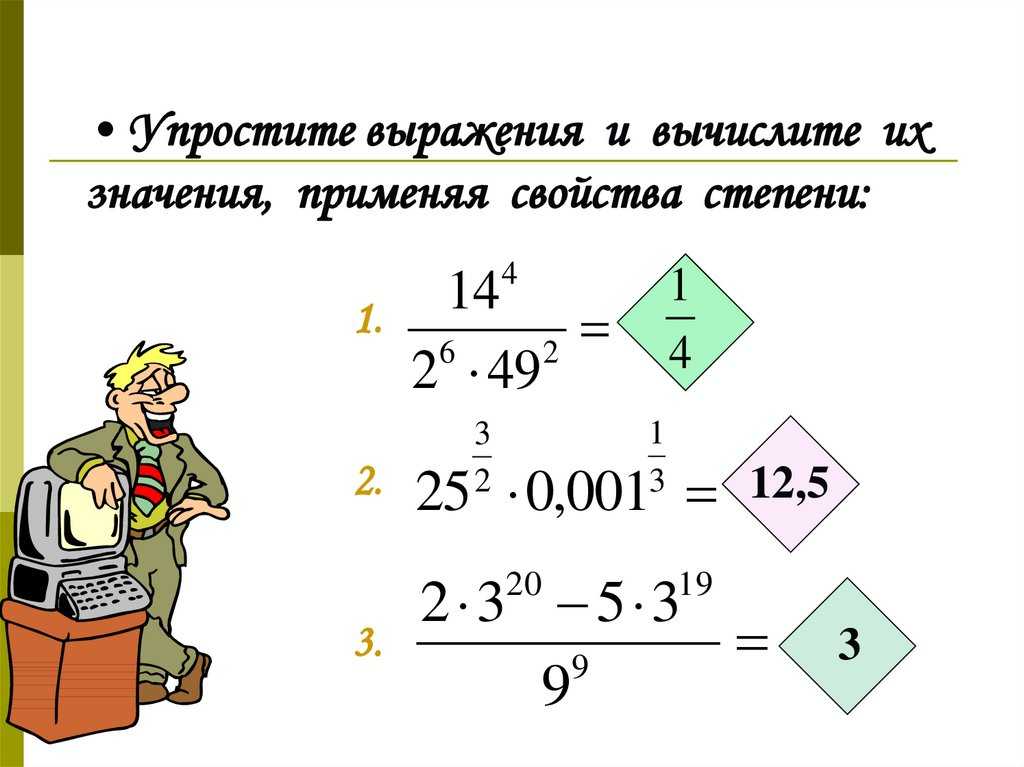
Для упрощения выражений с корнями используйте преобразования, такие как умножение и деление на сопряженные выражения.
Когда в выражении встречаются степени с одинаковыми основаниями, применяйте правило: a^m * a^n = a^(m+n).

Если у вас есть дробь с отрицательной степенью, помните, что a^(-n) = 1/a^n.

Используйте метод разделения на множители, чтобы упростить выражения с дробями и степенями.

Не забывайте о распределительном законе при работе с выражениями, содержащими степени и дроби.
