Объяснение принципа работы тригонометрического круга для вычисления синуса углов

Тригонометрический круг — это важный инструмент в математике, который помогает наглядно понять связи между углами и их тригонометрическими функциями. На этой странице вы найдете полезные советы и изображения, которые помогут вам разобраться, как с помощью тригонометрического круга вычислять синус углов, включая такие важные моменты, как значение синуса при угле π и его роль в различных задачах.

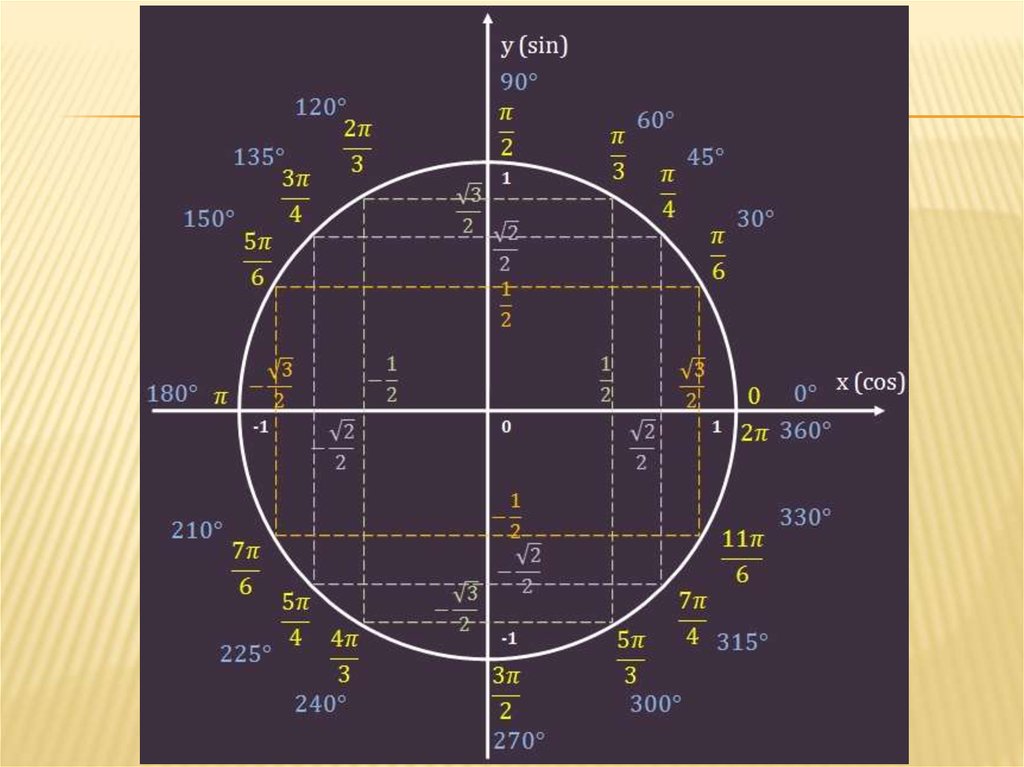
Для правильного вычисления синуса на тригонометрическом круге важно точно понимать, где расположен угол, и как его проекция на ось Y соотносится с радиусом круга.

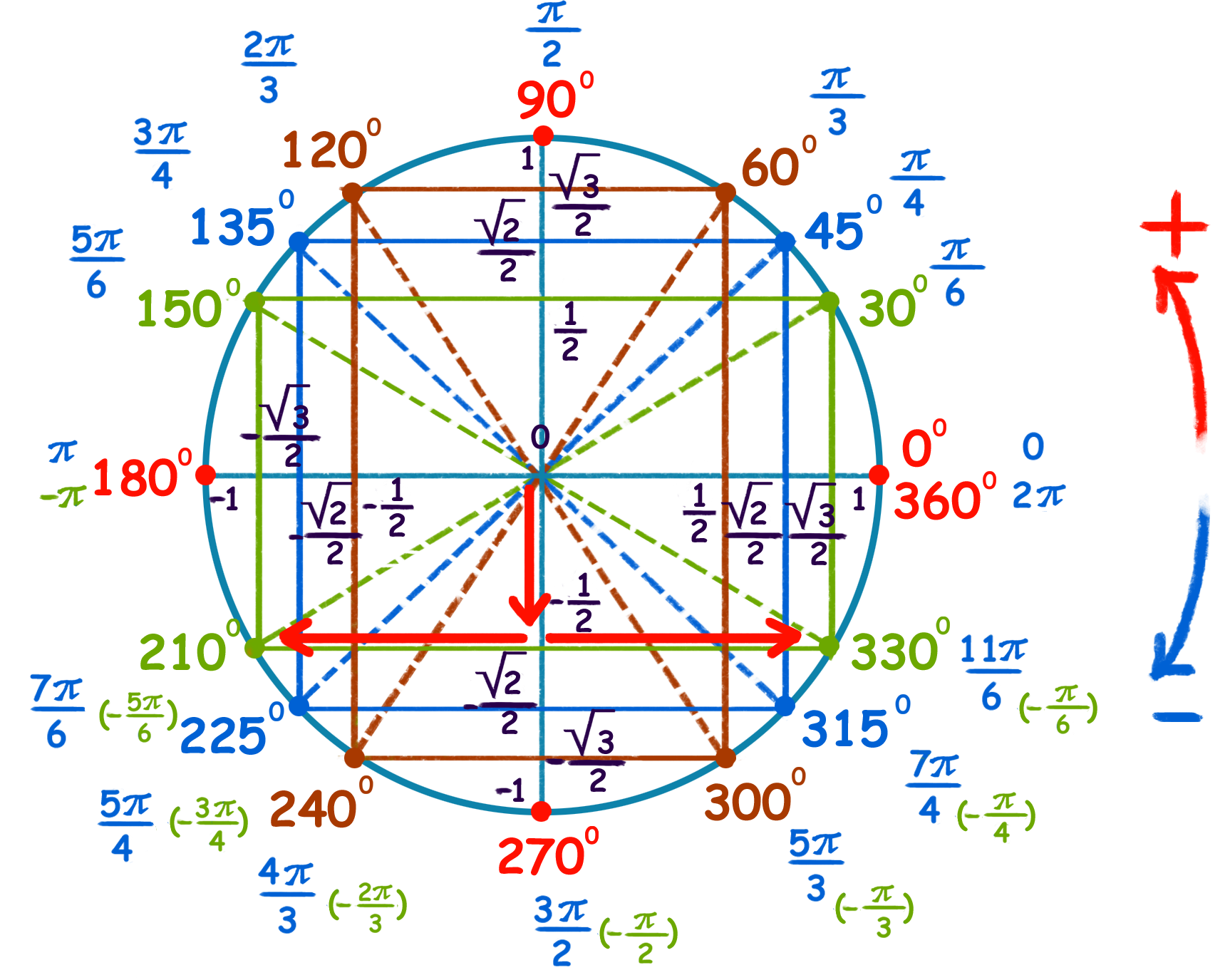
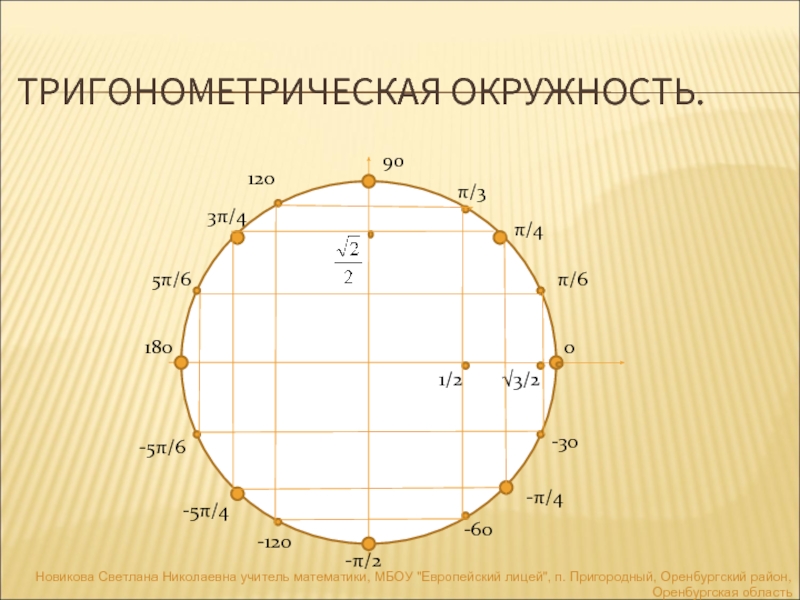
Не забывайте, что синус угла π равен нулю, так как проекция на ось Y для этого угла будет находиться на нулевой отметке.

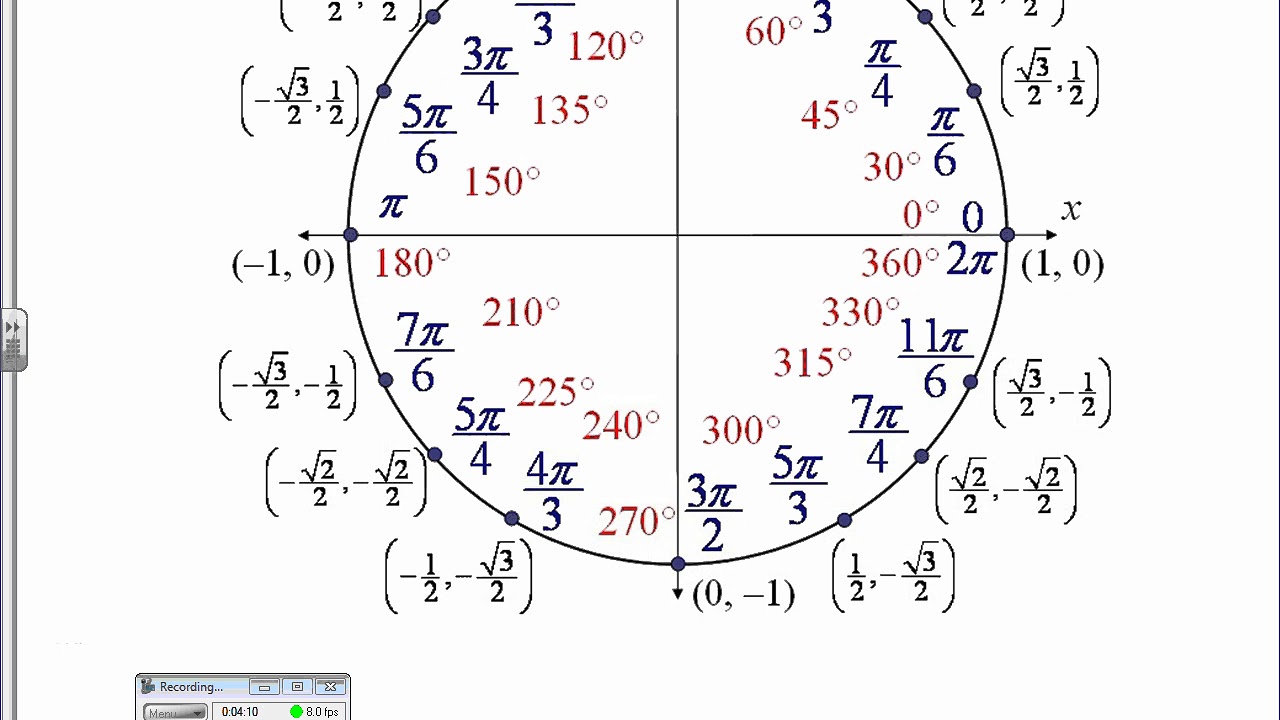
Обратите внимание, что синус угла 0 и угла π имеют одинаковое значение, но противоположные знаки на разных полусферах.

Для точного вычисления синуса углов в радианах используйте стандартный диапазон от 0 до 2π, чтобы избежать ошибок при интерпретации углов.

Чтобы запомнить значения синуса для стандартных углов (π/2, π, 3π/2, 2π), попробуйте визуализировать их на тригонометрическом круге или сделать карточки с основными значениями.

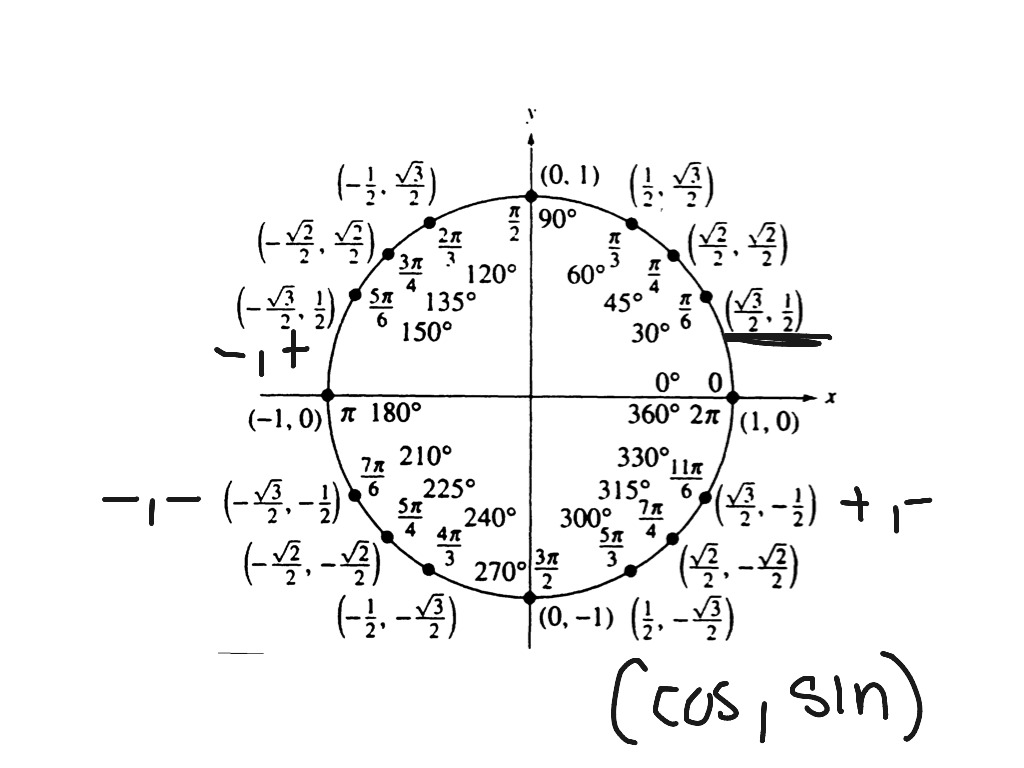
Для углов больше 2π или меньше 0, важно учесть периодичность тригонометрических функций: синус повторяет свои значения каждые 2π радиан.

Помните, что синус угла всегда лежит в пределах от -1 до 1, вне зависимости от величины угла.

При работе с тригонометрическим кругом полезно использовать симметрию: синус одинаковых углов, но с разными знаками, будет иметь зеркальное отражение относительно оси X.

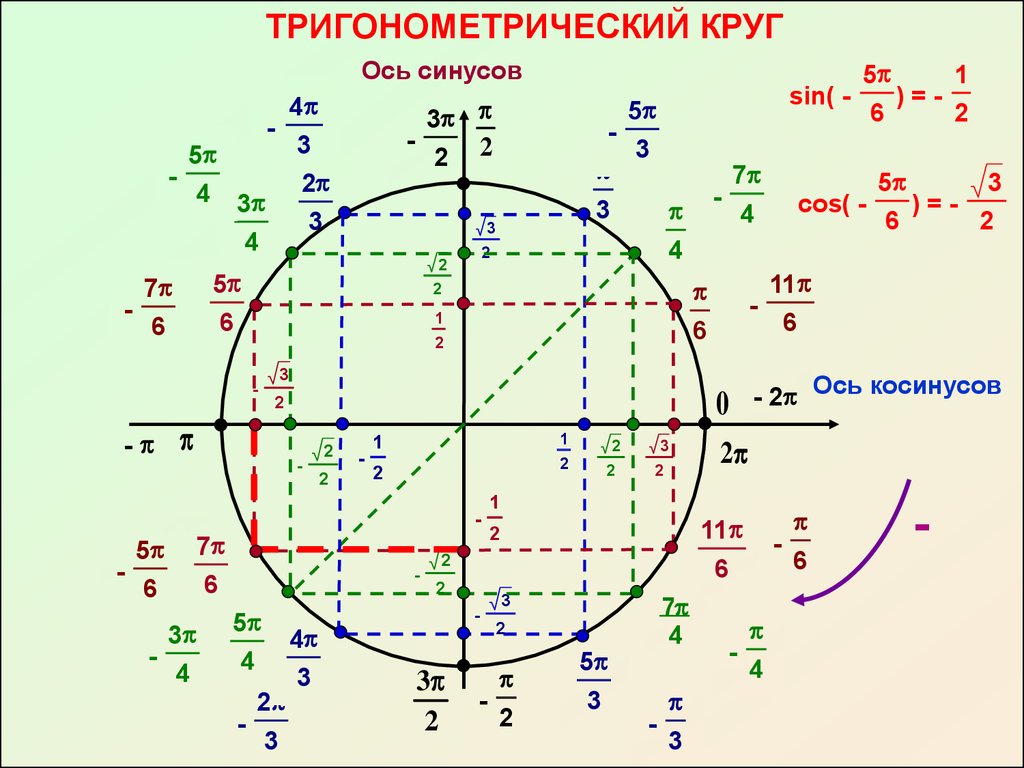
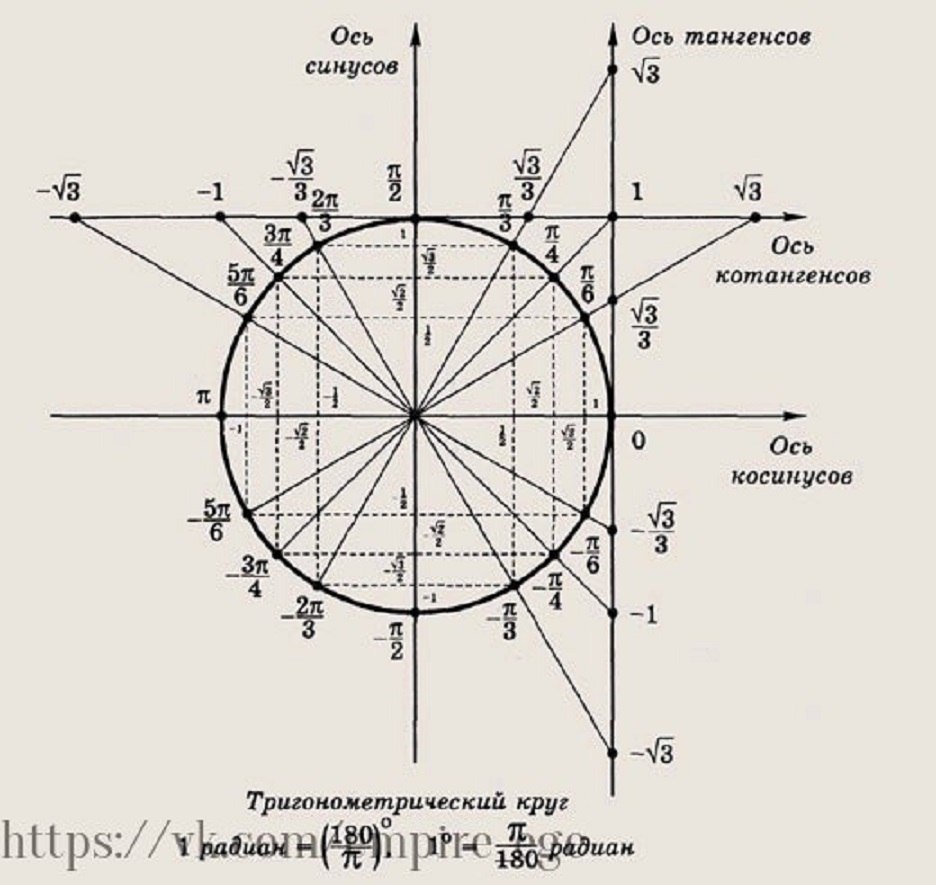
Визуализация значений синуса для разных углов помогает лучше запомнить их особенности, поэтому регулярное рисование тригонометрического круга значительно ускоряет обучение.

При решении задач на нахождение синуса углов важно четко понимать, в какой четверти находится угол, так как это влияет на знак значения синуса.