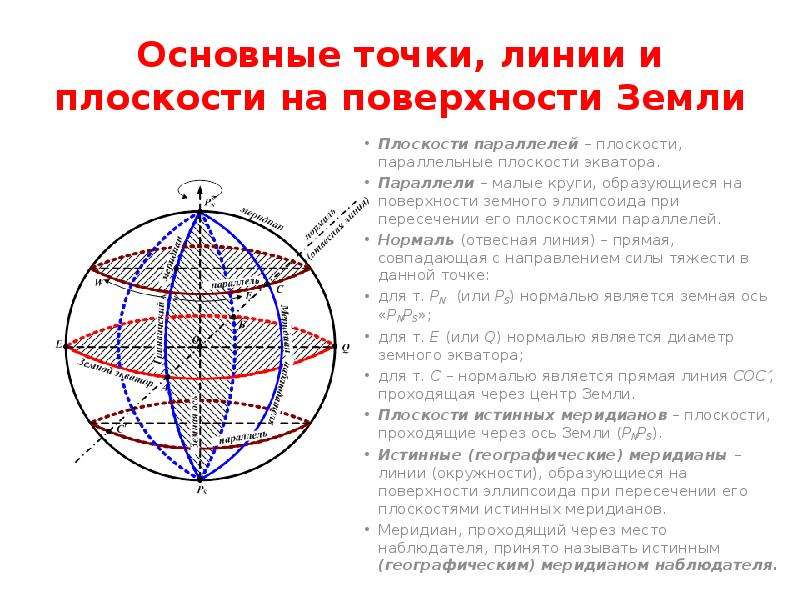
Как точки и линии определяют геометрические объекты на плоскости: практические рекомендации
На этой странице собраны полезные советы и иллюстрации, которые помогут лучше понять ключевые аспекты геометрии, связанные с точками и линиями на плоскости. Здесь вы найдете различные практические рекомендации и примеры, которые помогут углубить знания в этой области.
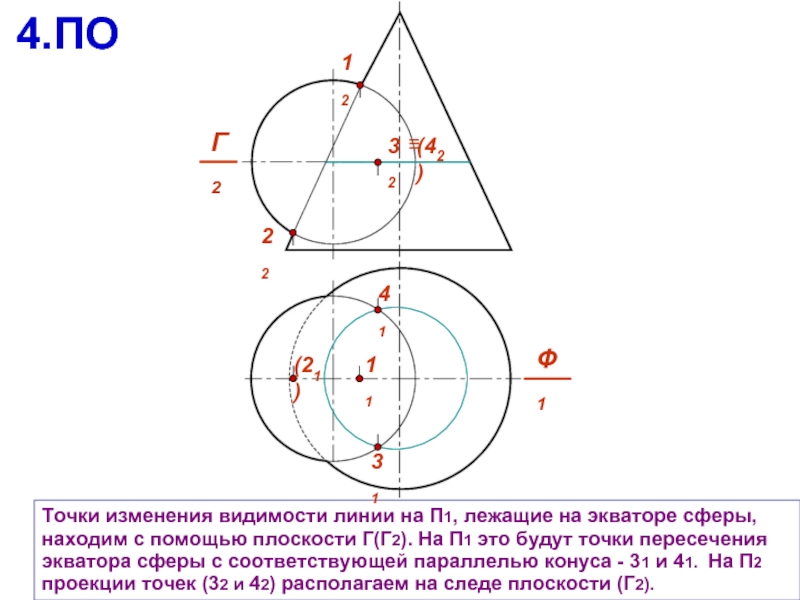
Точки на плоскости могут служить основой для построения других геометрических объектов, таких как прямые и окружности.

Василий Кандинский: \
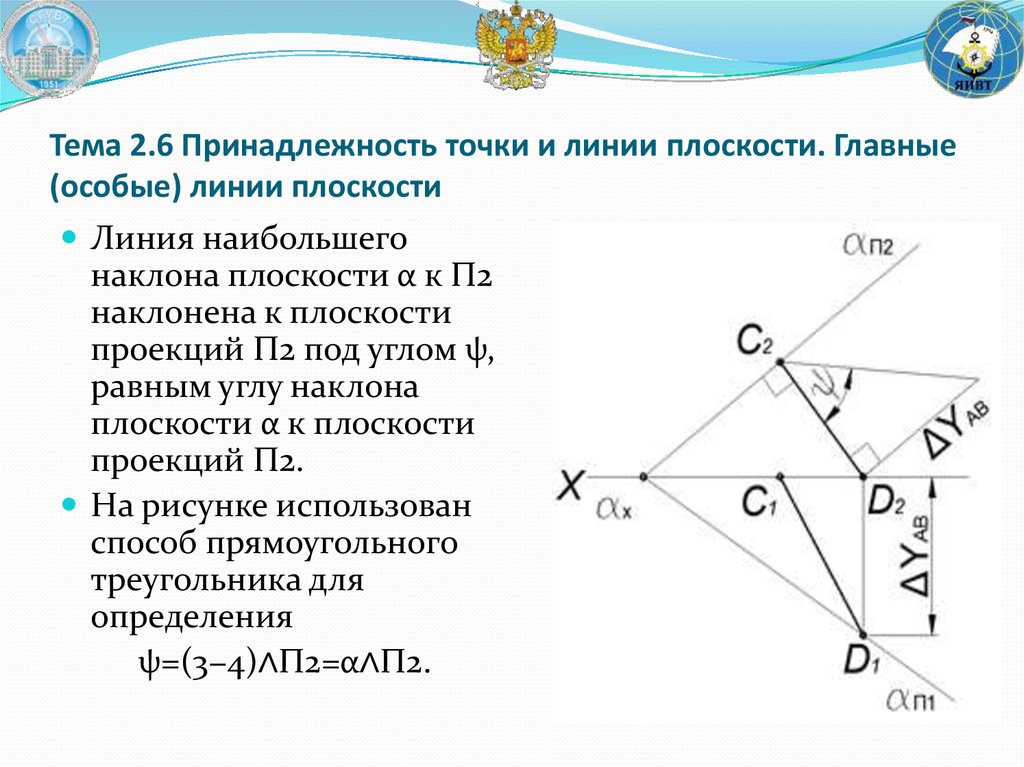
Линия на плоскости может быть представлена как множество точек, удовлетворяющих определенному математическому условию.

Василий Васильевич меняет профессию. Точка и линия на плоскости [Литобзор] #15 подкаст LAMP

При анализе взаимного расположения точек и линий важно учитывать такие элементы, как угол наклона и пересечения.

Отзыв о книге Василий Кандинский - Точка и линия на плоскости
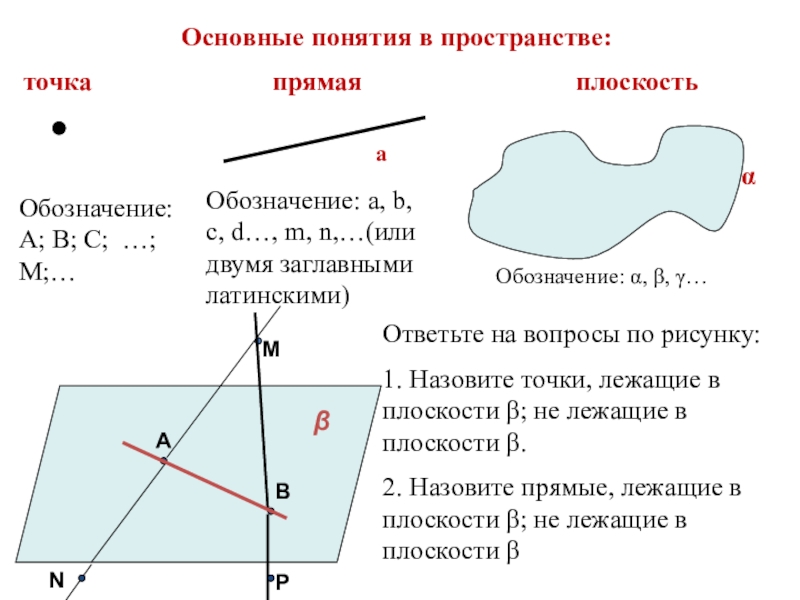
Для построения геометрических фигур всегда начинайте с определения ключевых точек, которые будут служить ориентирами для остальных элементов.

Живое Искусство #7. Кандинский. Точка. Линия. Плоскость.

Помимо прямых линий, существуют кривые линии, такие как окружности или эллипсы, которые также могут быть описаны через взаимодействие точек на плоскости.

Точки и линии
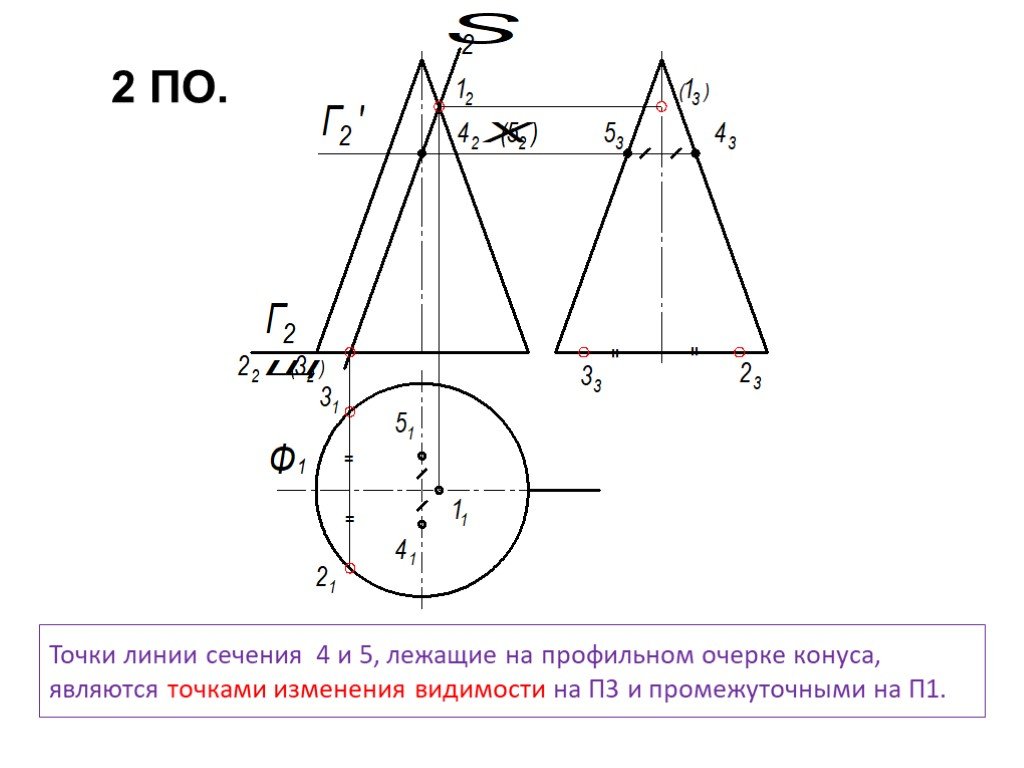
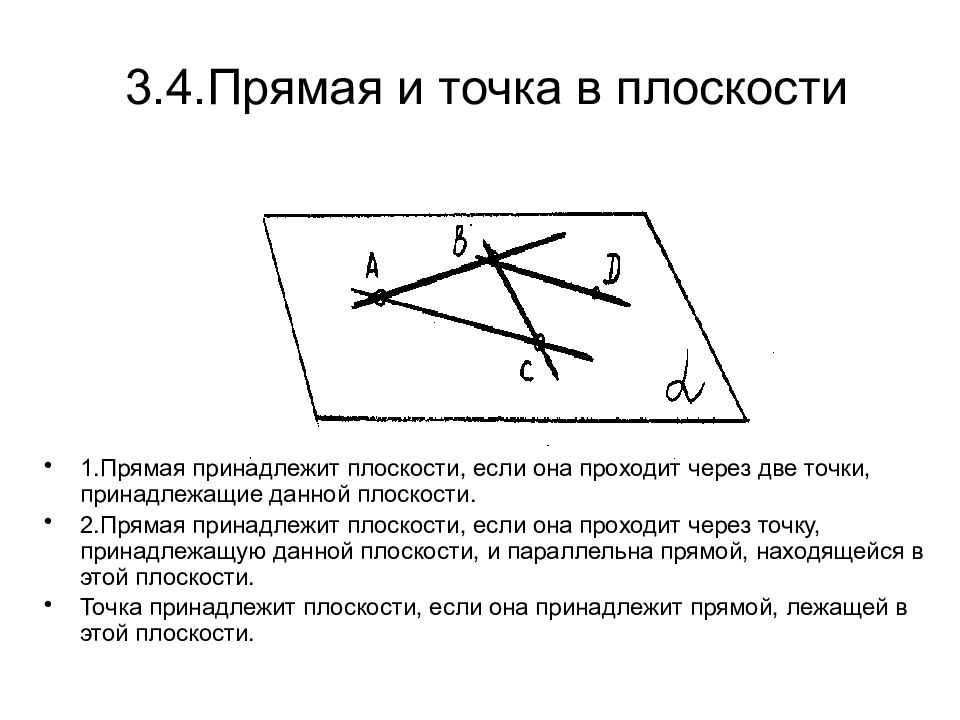
Для точных вычислений используйте координатную систему, где каждая точка на плоскости имеет свои уникальные координаты.
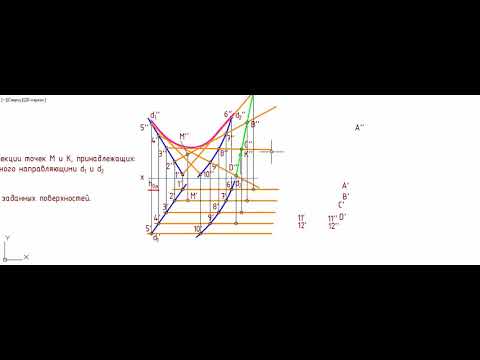
Точка и линия на поверхности
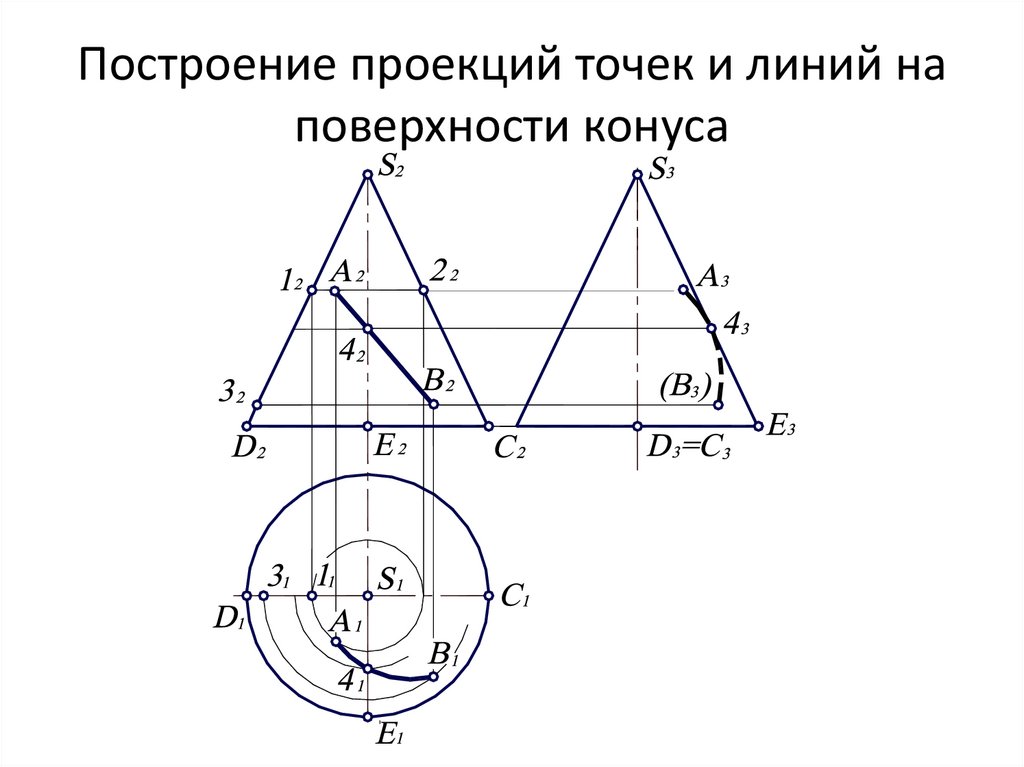
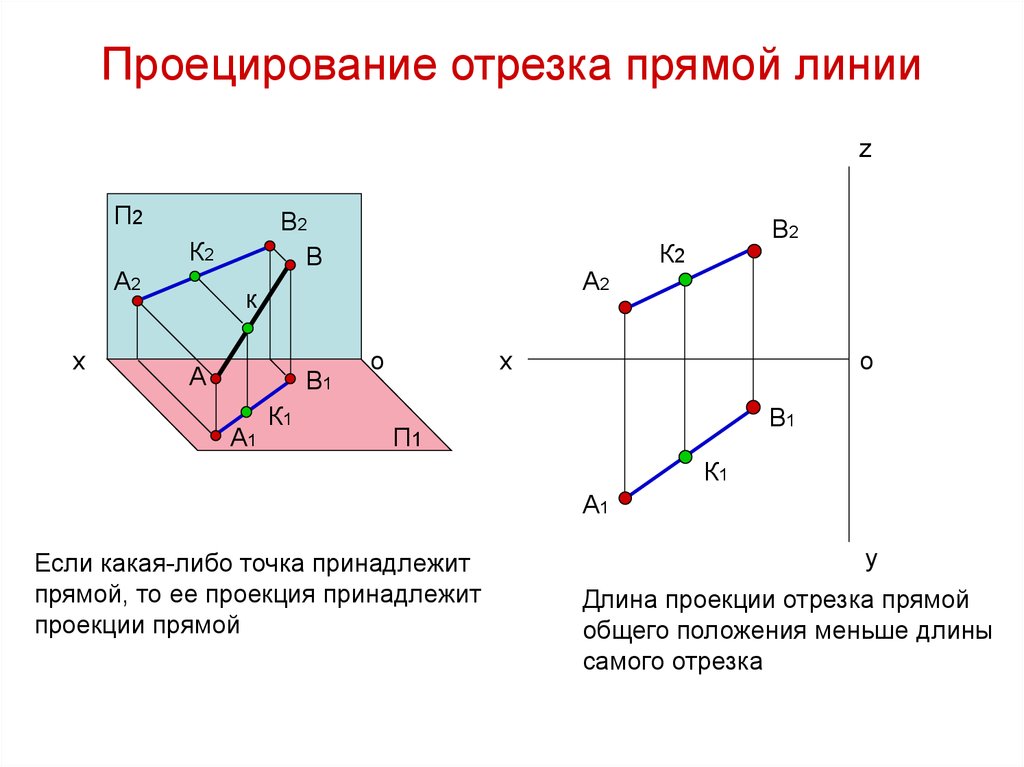
Когда точка лежит на линии, это означает, что координаты этой точки удовлетворяют уравнению линии.

Библиотека иллюстратора: «Точка и линия на плоскости», В. Кандинский
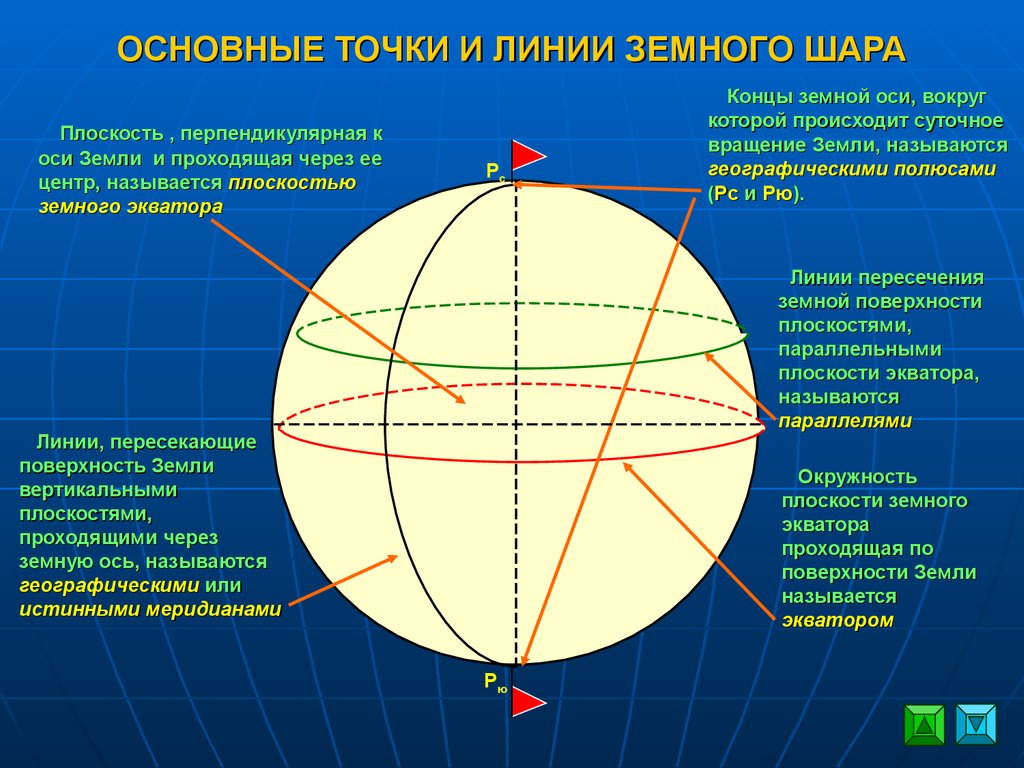
Прямые линии могут быть параллельными, пересекающимися или совпадающими, что важно для анализа геометрических задач.
Чтобы убедиться, что три точки не лежат на одной прямой, можно использовать критерий коллинеарности, проверив их координаты.

Точка Сборки

Изучая точки и линии на плоскости, полезно обращаться к классическим геометрическим теоремам, таким как теорема Пифагора и свойства подобных треугольников.

Точка сборки