Таблица углов в градусной и радианной мере: все важные значения для математических расчетов
На этой странице представлена подробная таблица углов, выраженных как в градусах, так и в радианах. Этот инструмент поможет вам быстро ориентироваться в различных математических и физических задачах, где требуется преобразование между этими двумя единицами измерения углов. Мы подготовили полезные советы по использованию таблицы и удобному запоминанию значений.


При использовании таблицы для преобразования углов из градусов в радианы и обратно, помните, что один радиан равен 180°/π.

Что такое радиан?
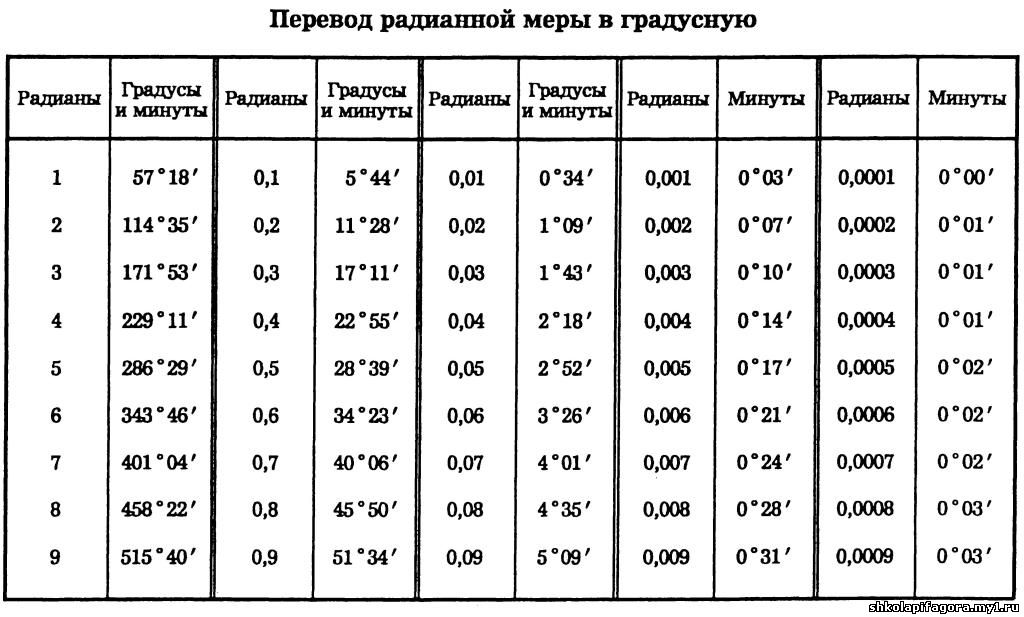

Для запоминания ключевых углов в радианах используйте округленные значения, такие как π/6, π/4, π/3 и π/2.

Выразить углы из радиан в градусы и из градусов в радианы.
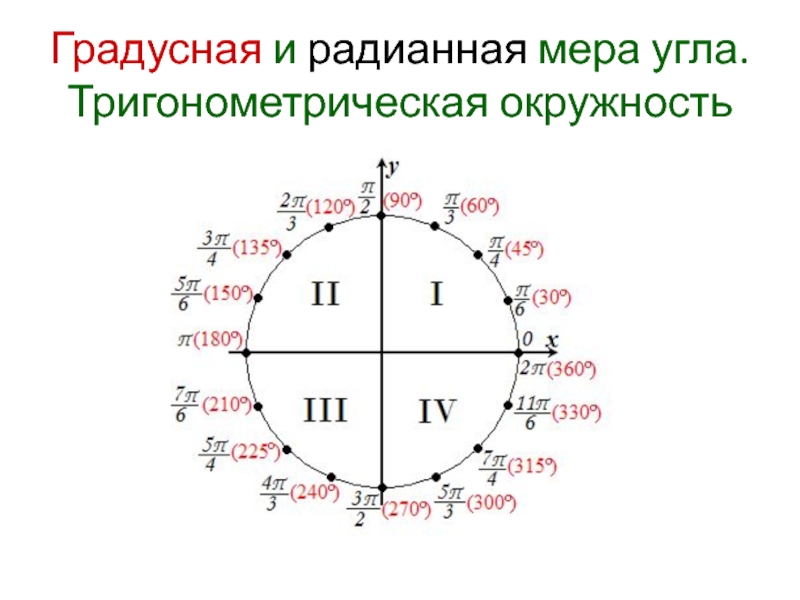
Чтобы быстрее ориентироваться в таблице, обращайте внимание на стандартные углы (0°, 30°, 45°, 60°, 90° и т.д.).

Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 класс

Если вам нужно перевести угол из радиан в градусы, умножьте его на 180° и разделите на π.

Перевод радианной меры углов в градусную

Для углов, превышающих 360° (или 2π радиан), используйте модуль, чтобы получить эквивалент угла в пределах одного круга.

Вся аналитика по параметрам за 5 часов. ЕГЭ 2025 Математика. Задача 18

Помните, что π приближенно равно 3.1416, а это знание поможет вам ускорить вычисления.
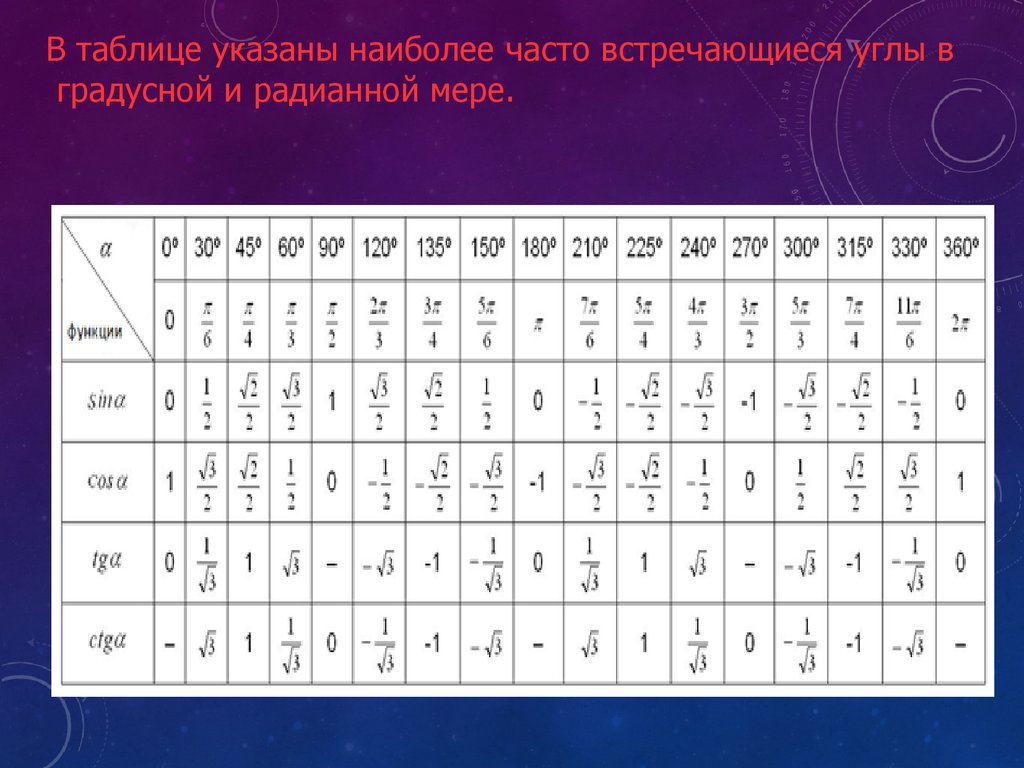
Для более удобного восприятия значений радианов можно запомнить их графически, используя круговые диаграммы.
При решении задач на преобразование углов, всегда проверяйте, в какой системе измеряются исходные данные: градусная или радианная.
Запись радианной меры угла в градусной
Если вы работаете с углами в тригонометрии, полезно знать стандартные значения синуса и косинуса для ключевых углов, таких как 0°, 30°, 45°, 60°, 90°.

Практикуйтесь в быстром переводе углов между системами, чтобы лучше ориентироваться в математических задачах и улучшить навыки решения проблем.