Сюръективное отображение: примеры, свойства и полезные советы
Сюръективное отображение — это важное понятие математики, которое помогает определить, можно ли каждой точке множества назначения сопоставить хотя бы одну точку из множества отправления. В этой статье собраны наглядные примеры, фотографии и практические советы для лучшего понимания этого понятия.

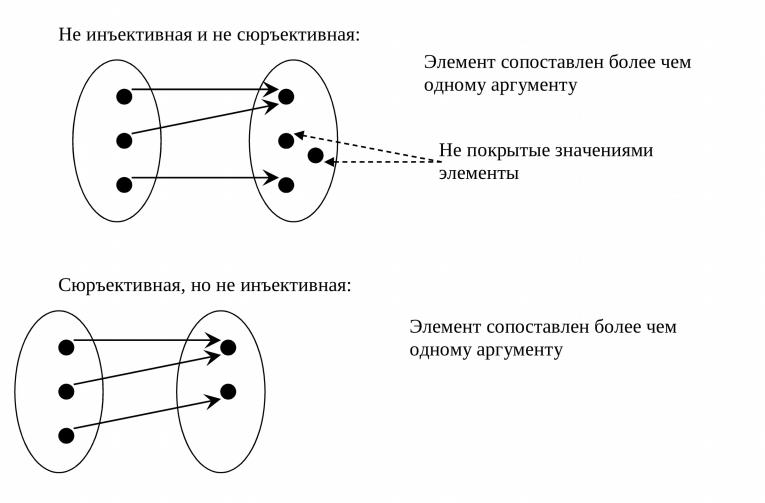
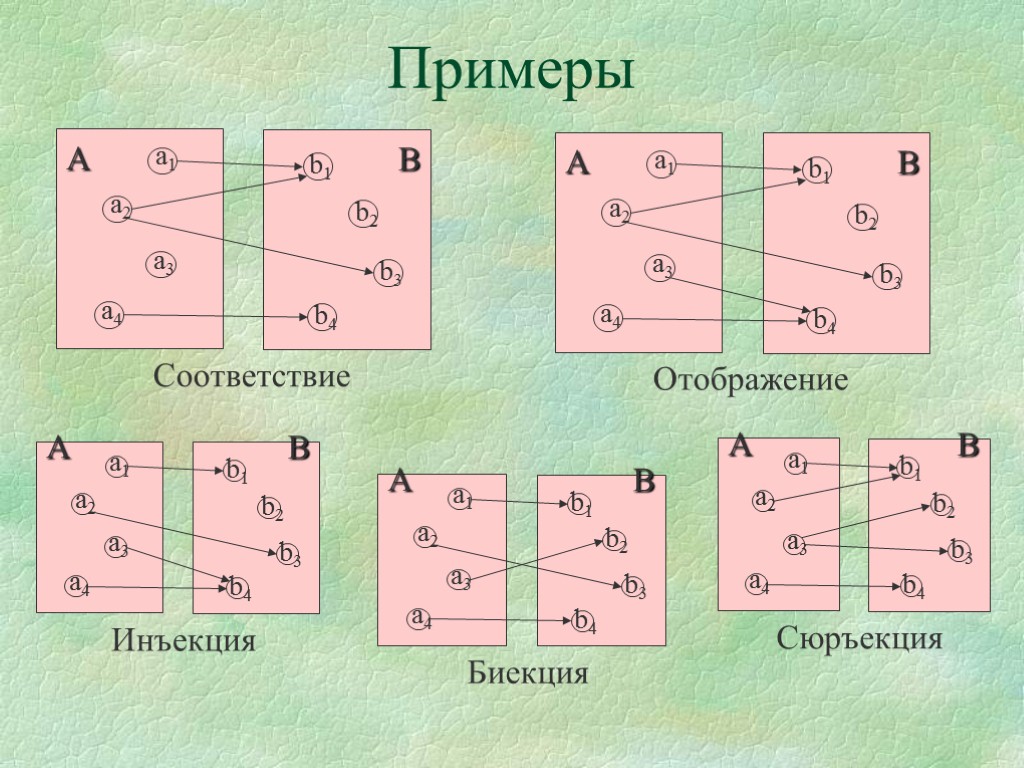
Всегда начинайте с определения: сюръекция — это функция, где каждое значение в целевом множестве имеет хотя бы один прообраз.

Отображение. Характеристическая функция. Свойства.


Проверяйте сюръективность функции, решая уравнение вида f(x) = y для любого y из множества значений.
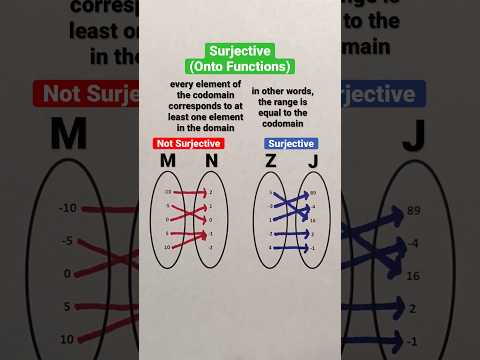
Surjective (Onto Functions) #Shorts #math

Используйте графики: визуализация помогает лучше понять, какие области множества отображаются.

Соответствия и функции

Помните, что сюръекция возможна только при совпадении или превышении мощности множества определения над множеством значений.

Отображения множеств
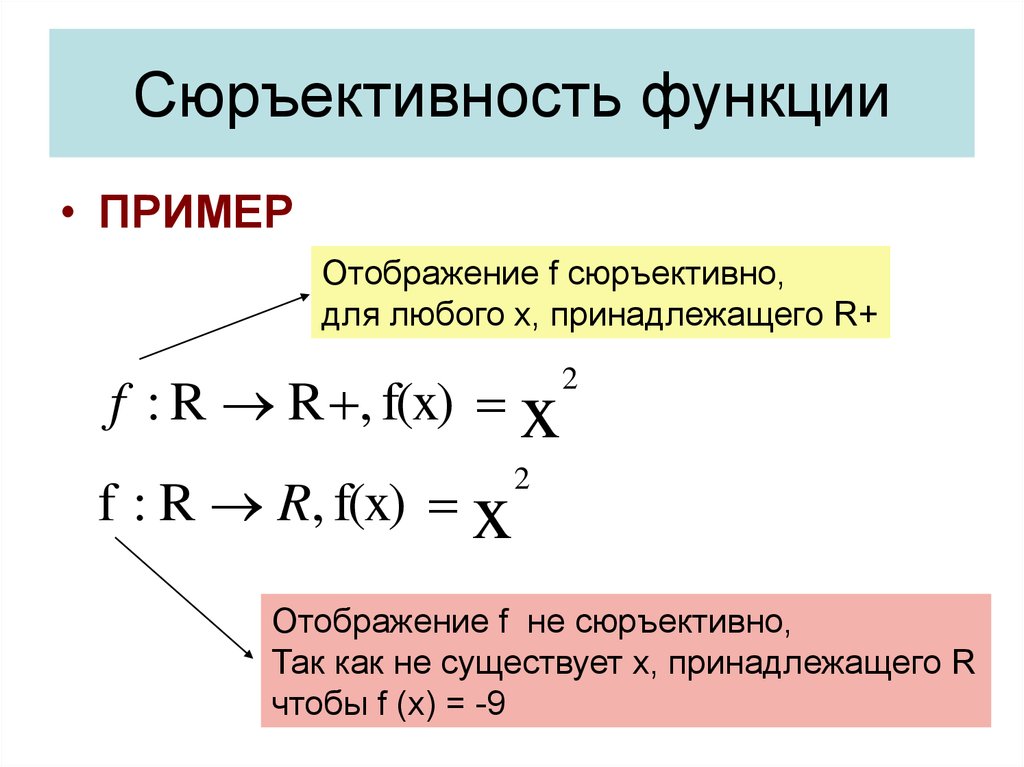
Примеры из реальной жизни: распределение студентов по группам — пример сюръективного отображения.
A.3.1 Понятие функции

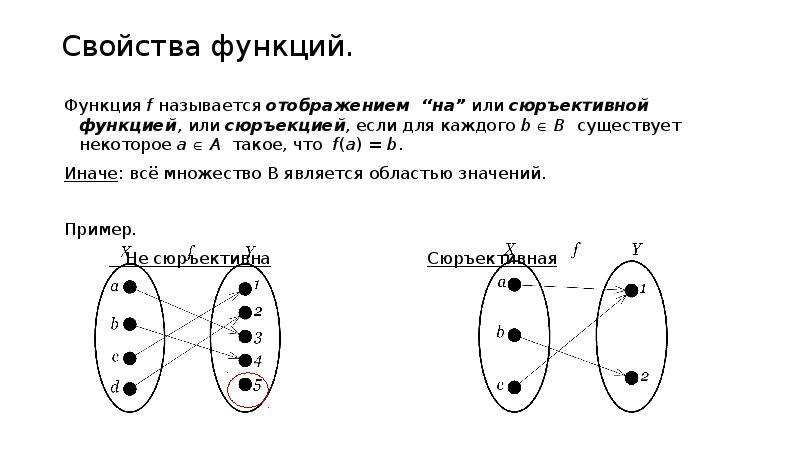
Учитесь находить контрпримеры, чтобы быстро исключать несюръективные функции.

Попробуйте отобразить простые линейные функции, чтобы закрепить базовые принципы.

Немного об отображениях. Инъекция, сюръекция и биекция - Курс молодого бойца - Занятие 4

Изучайте связанные понятия, такие как инъекция и биекция, для полного понимания функций.

12 Инъекция, сюрьекция, биекция - Роман Попков - ИТМО
Проверяйте практические задачи: как функция распределяет ресурсы, и является ли это сюръективным отображением.
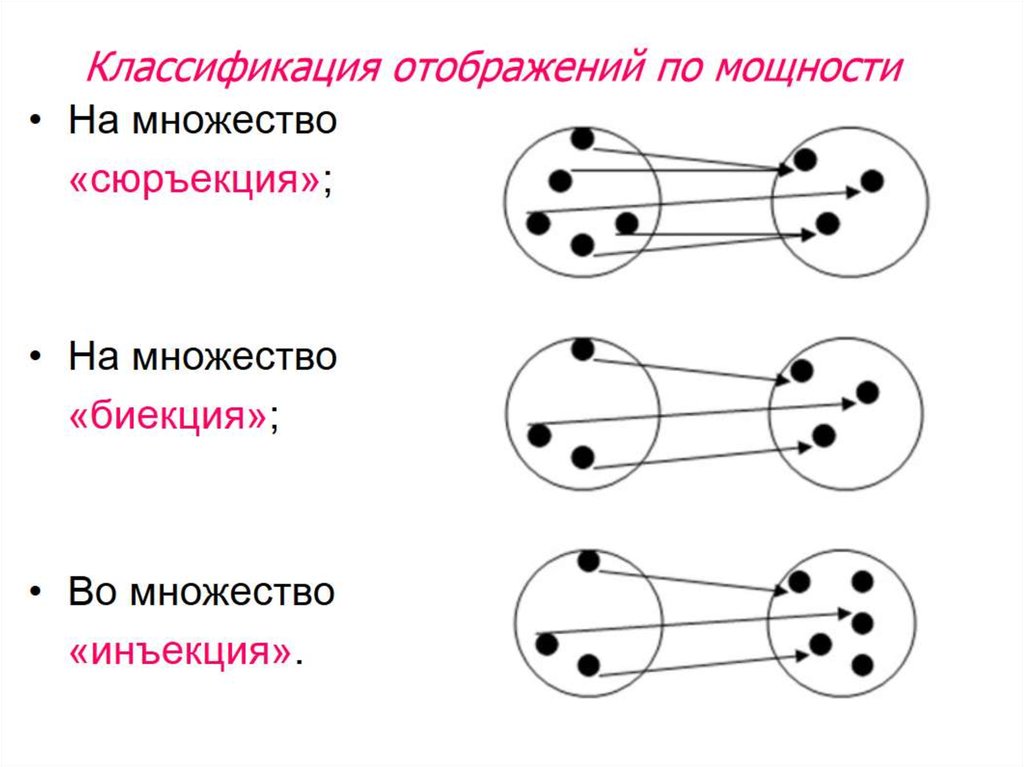
Задавайте вопросы: «Все ли значения в целевом множестве используются?» Это ключ к пониманию сюръекции.
Функции: инъекция, сюръекция и биекция


ОКТЧ 2. Отображения и соответствия