Как работают свойства внешней биссектрисы в геометрии: от теории до практики
Внешняя биссектрисы угла – это важный элемент геометрии, который обладает рядом уникальных свойств. В этой статье мы рассмотрим теоремы, связанные с внешней биссектрисой, а также примеры ее применения в решении геометрических задач.
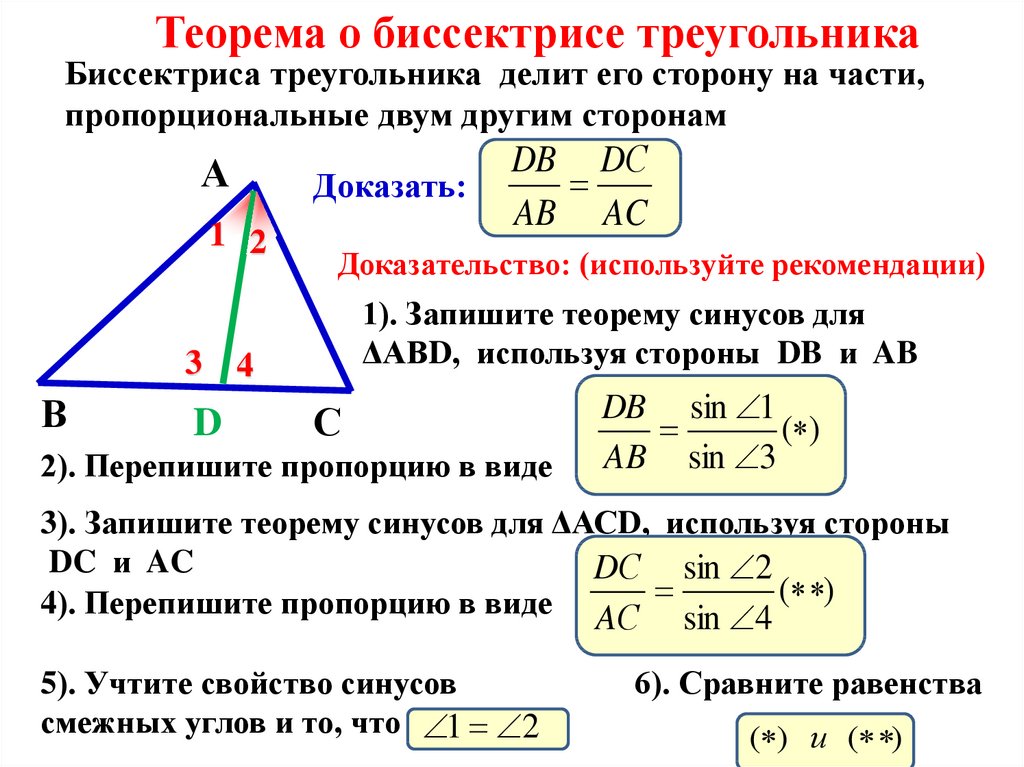
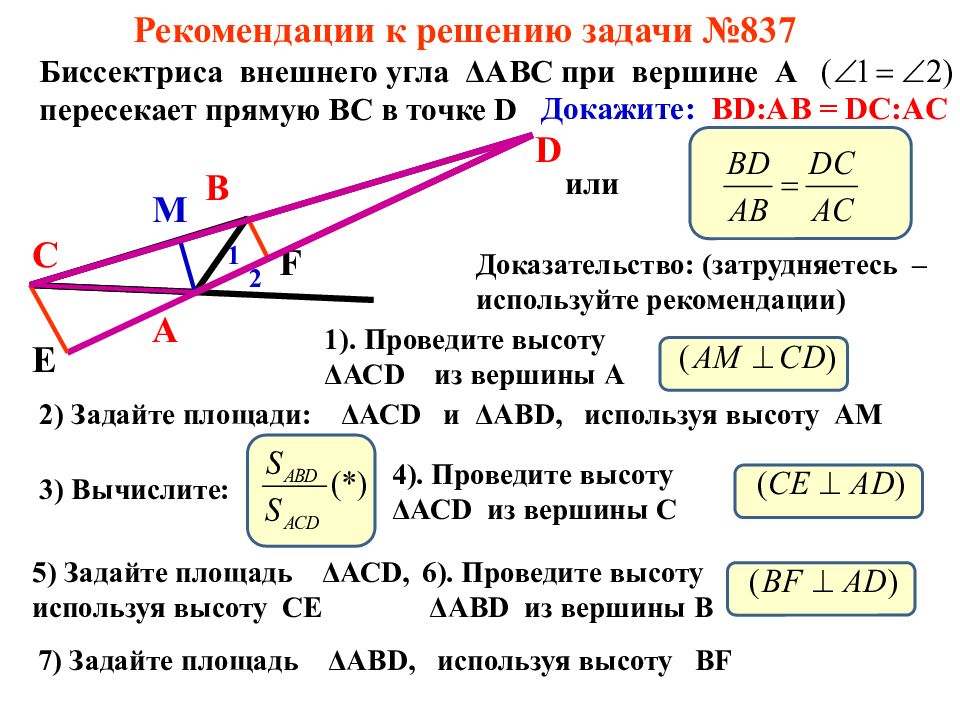
Для работы с внешней биссектрисой важно понимать ее геометрическое положение относительно угла и смежных сторон.

Урок по теме СВОЙСТВА БИССЕКТРИСЫ УГЛА 8 КЛАСС ГЕОМЕТРИЯ
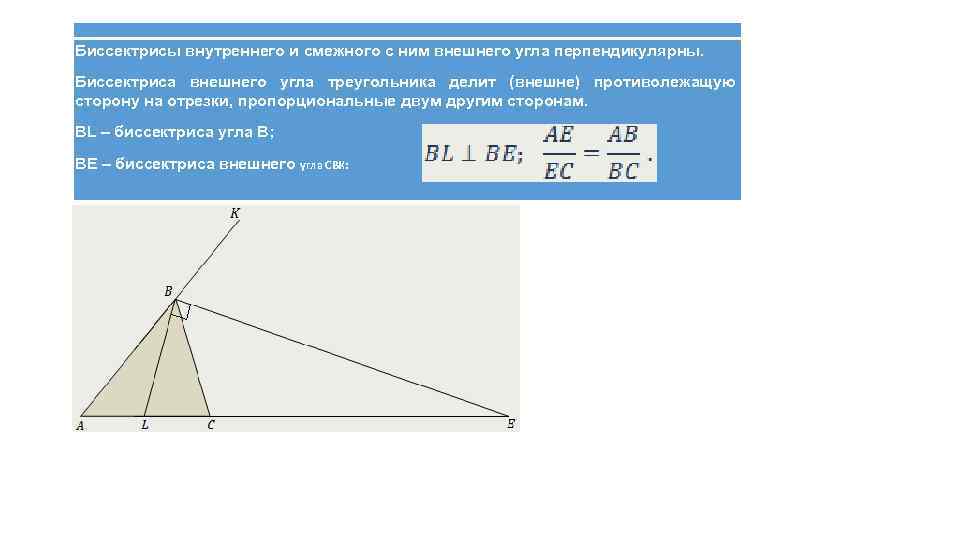
Помните, что внешняя биссектрисса делит внешний угол на два равных угла, что позволяет использовать это свойство для решения различных задач.

ЕГЭ 2023 по математике. №1,16 Замечательные свойства биссектрисы
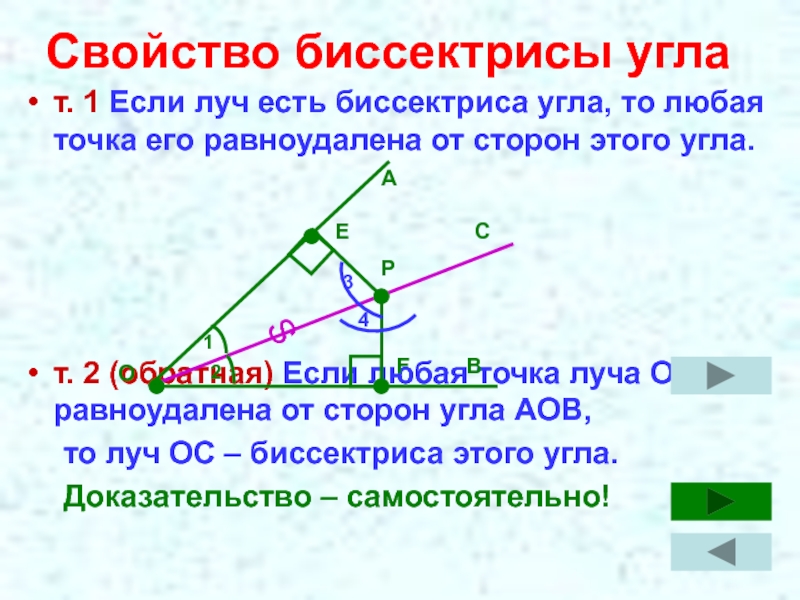
При построении внешней биссектрисы угла используйте точку пересечения биссектрисы с одной из сторон угла для точных расчетов.
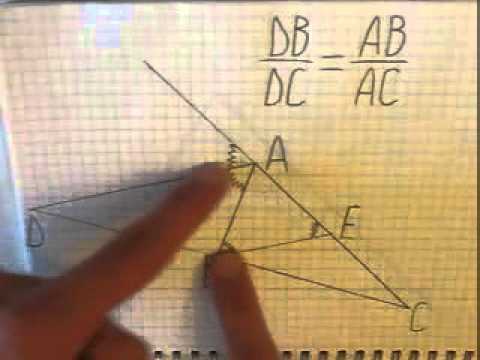
Теорема о свойстве биссектрисы внешнего угла треугольника Доказательство

Одно из основных свойств внешней биссектрисы – это теорема о пропорциональности отрезков, на которые она делит стороны угла.

Построение биссектрисы угла. 7 класс.
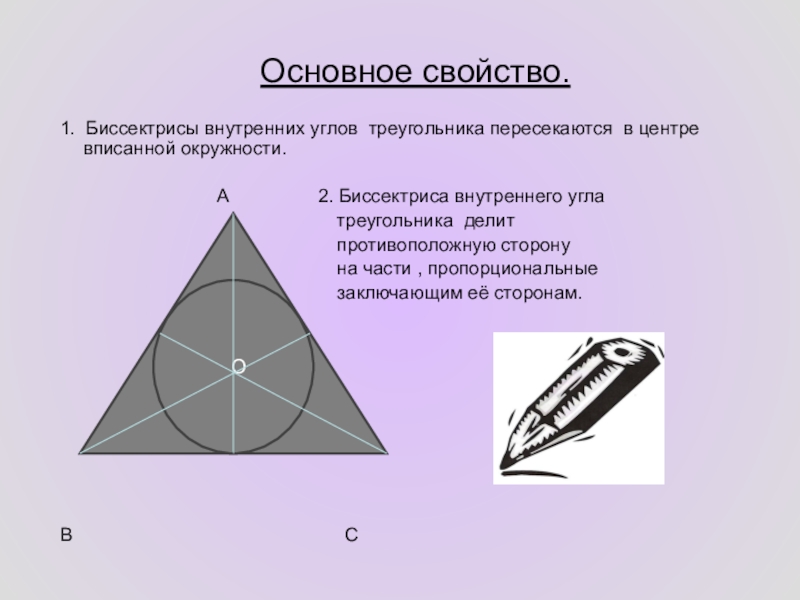
Чтобы эффективно использовать теорему о внешней биссектрисе, всегда проверяйте, что фигура является правильной, а углы – точными.

Длина медианы треугольника

При решении задач с внешней биссектрисой полезно использовать симметричные свойства углов, что позволяет упростить вычисления.
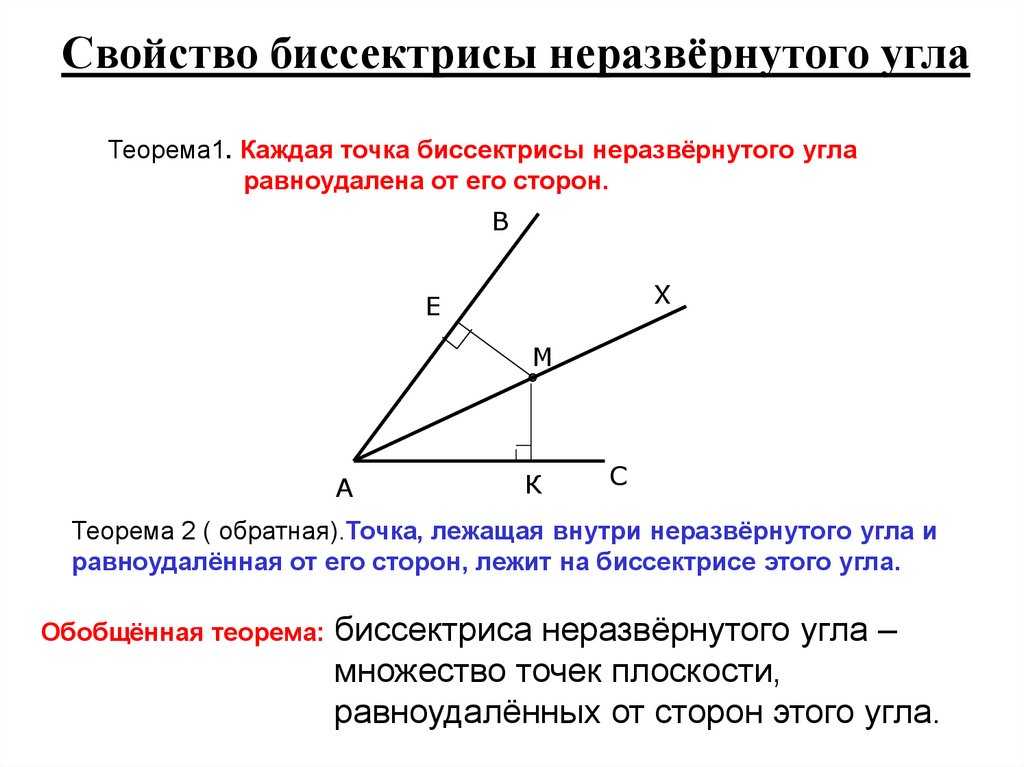

Не забывайте о связи внешней биссектрисы с кругами: она может быть полезной при нахождении центров окружностей, вписанных в многоугольники.
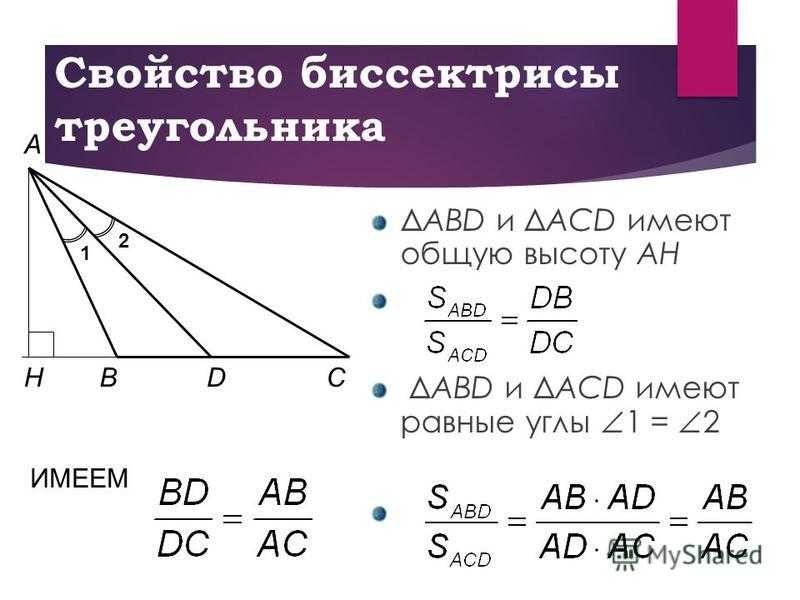

В некоторых задачах внешняя биссектрисса помогает находить коэффициенты пропорциональности между отрезками, что существенно упрощает решение.
Когда работаете с внешней биссектрисой, обращайте внимание на расположение сторон угла и их продолжение: это влияет на точность построения.


Используйте свойства внешней биссектрисы для нахождения точек пересечения, что может быть полезно в более сложных задачах с многогранниками.

8 класс, 35 урок, Свойства биссектрисы угла