Как использовать медианы для решения задач с треугольниками: советы и примеры
На этой странице вы найдете полезные советы и изображения, которые помогут вам лучше понять, что такое медианы треугольника, какие их свойства и как их можно использовать для решения различных геометрических задач. Медианы — это важные элементы треугольников, которые могут существенно упростить решение задач, связанных с центроидами, площадями и другими геометрическими характеристиками.

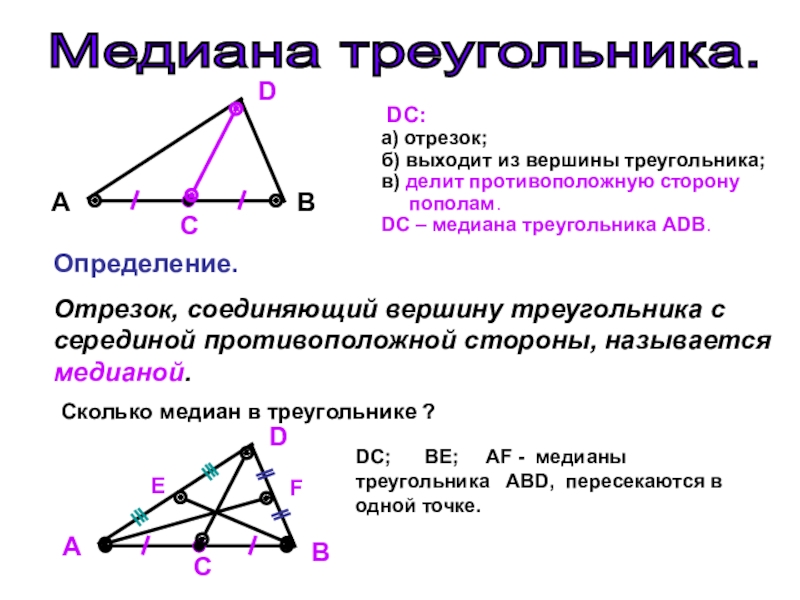
Чтобы найти медиану треугольника, необходимо провести отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

ВАЖНЫЕ свойства медиан треугольника #математика #математикаогэ #огэ #огэ2024 #shots #огэпоматематике
Для удобства в расчетах используйте координатный метод, который помогает найти точку пересечения медиан (центроид).
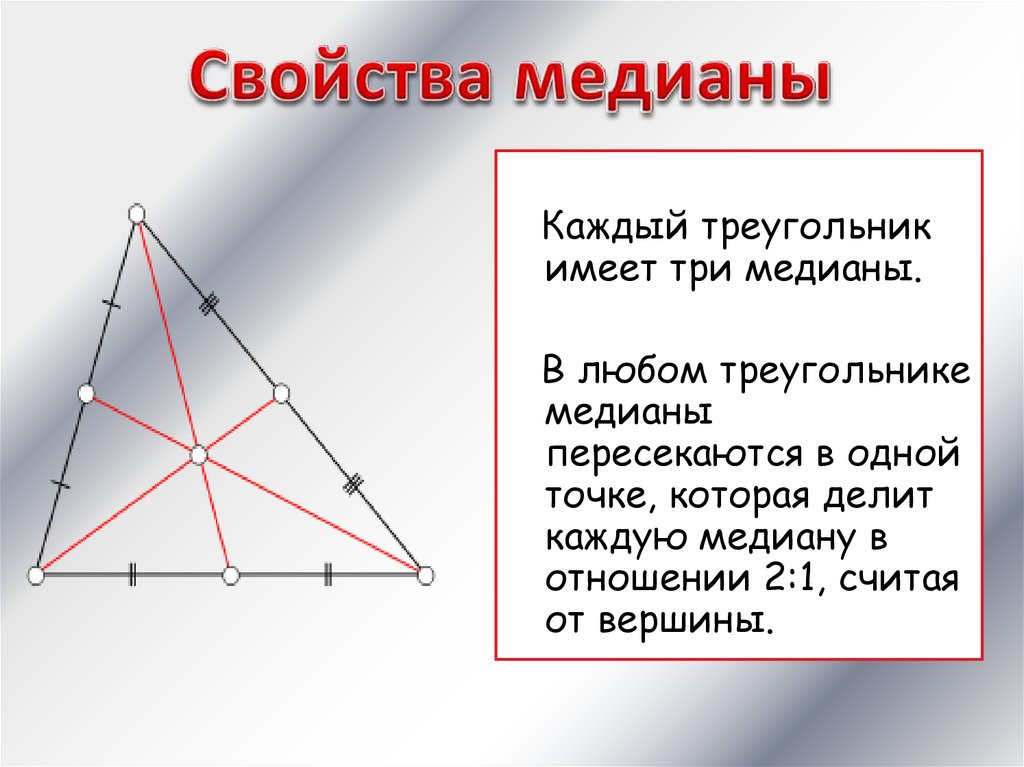
Точка пересечения медиан в треугольнике
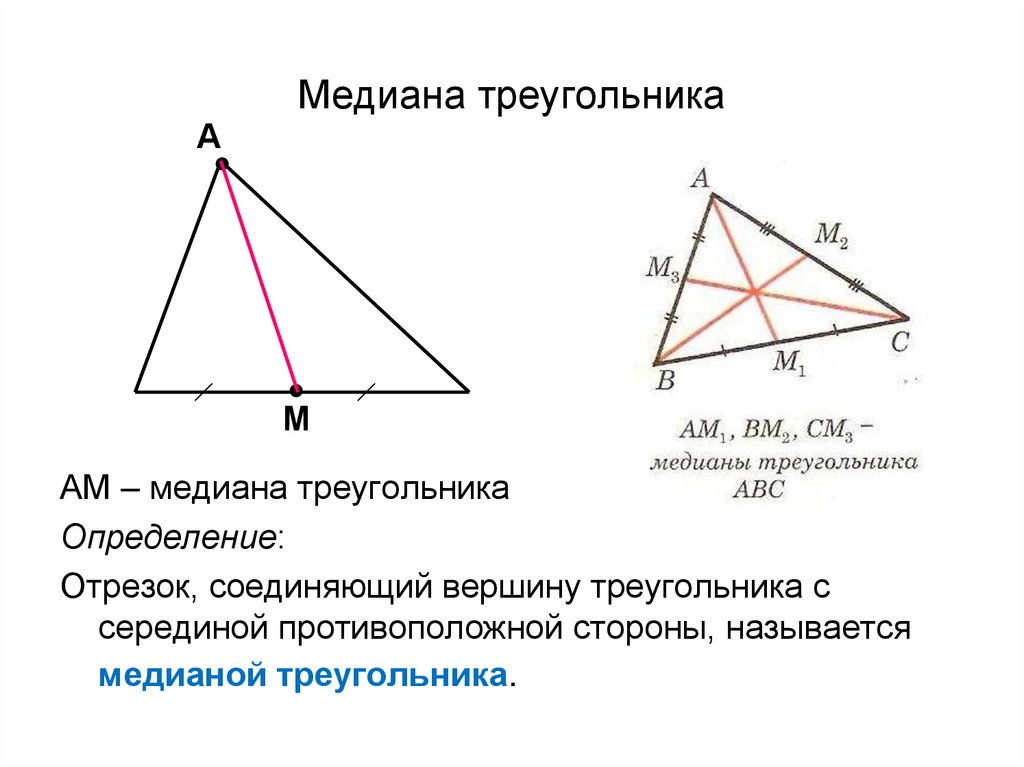
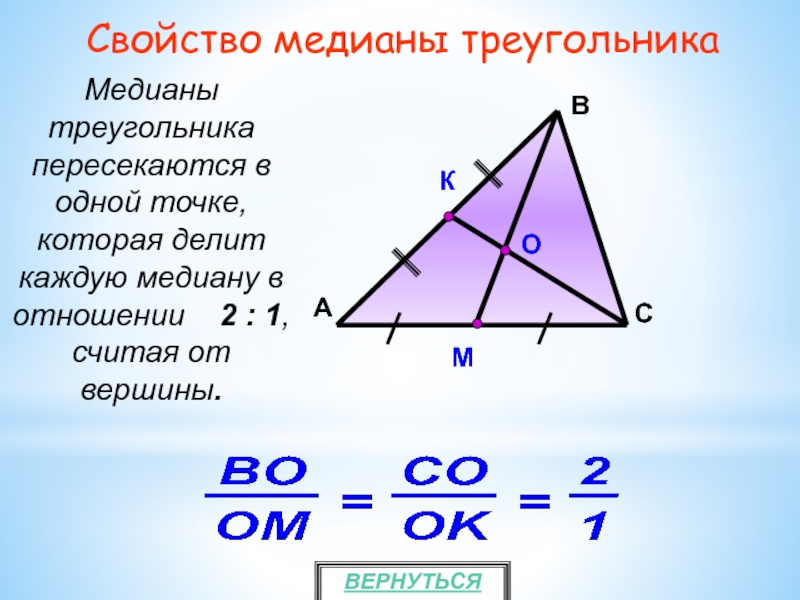
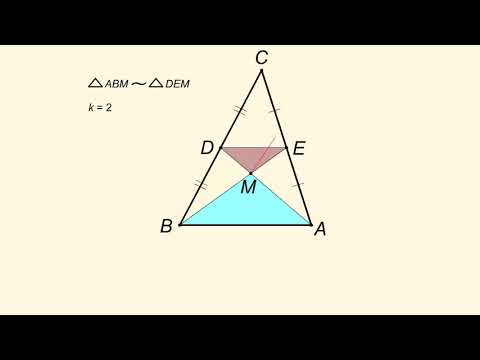
Помните, что все три медианы треугольника пересекаются в одной точке — центре масс или центроиде треугольника.

ЕГЭ база #15 / Треугольники и их элементы / Площадь треугольника / Свойства медиан / решу егэ

Медиана треугольника делит его на два треугольника, имеющие равные площади.
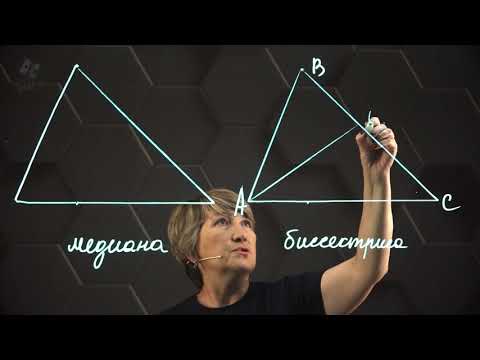
Высота, биссектриса, медиана. 7 класс.

Центроид треугольника всегда лежит на медианах и делит каждую из них в отношении 2:1, где большая часть находится ближе к вершине.

Урок 33. Свойство медиан треугольника (8 класс)
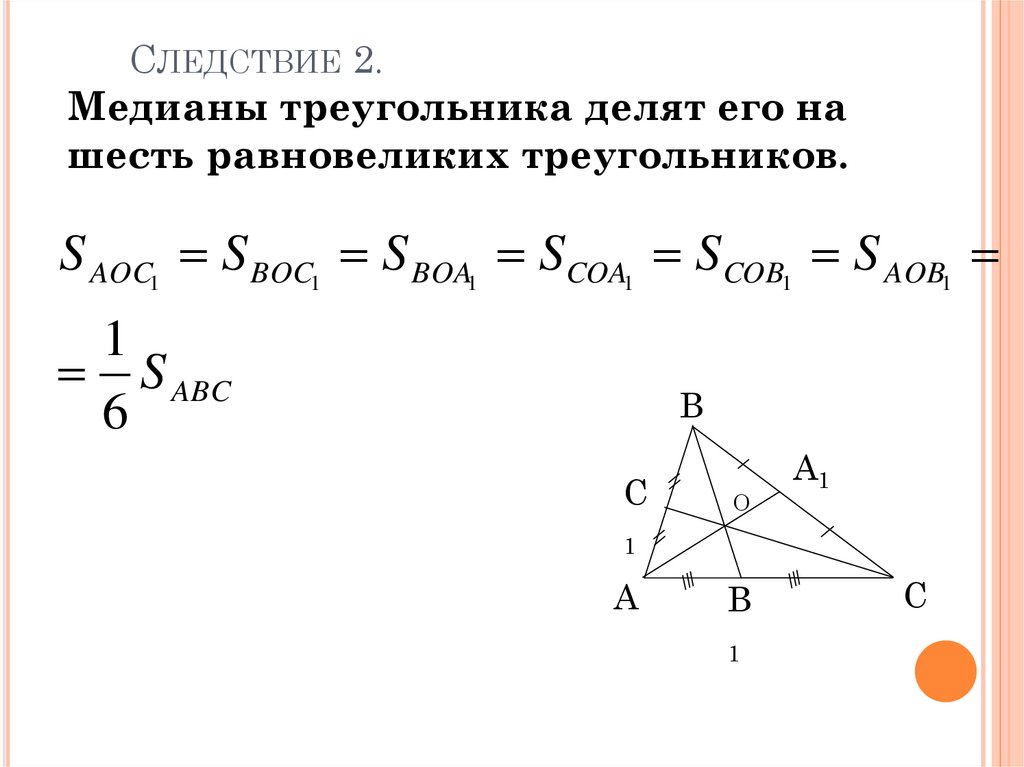
Используйте свойства медиан для нахождения равновесия в системах, моделирующих физические процессы, такие как центры масс.

ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.
Зная длины медиан, можно вычислить площадь треугольника, используя формулу Герона, если известны дополнительные параметры.

Для построения медиан в треугольнике можно использовать прямоугольную сетку, что упростит расчеты и визуализацию.
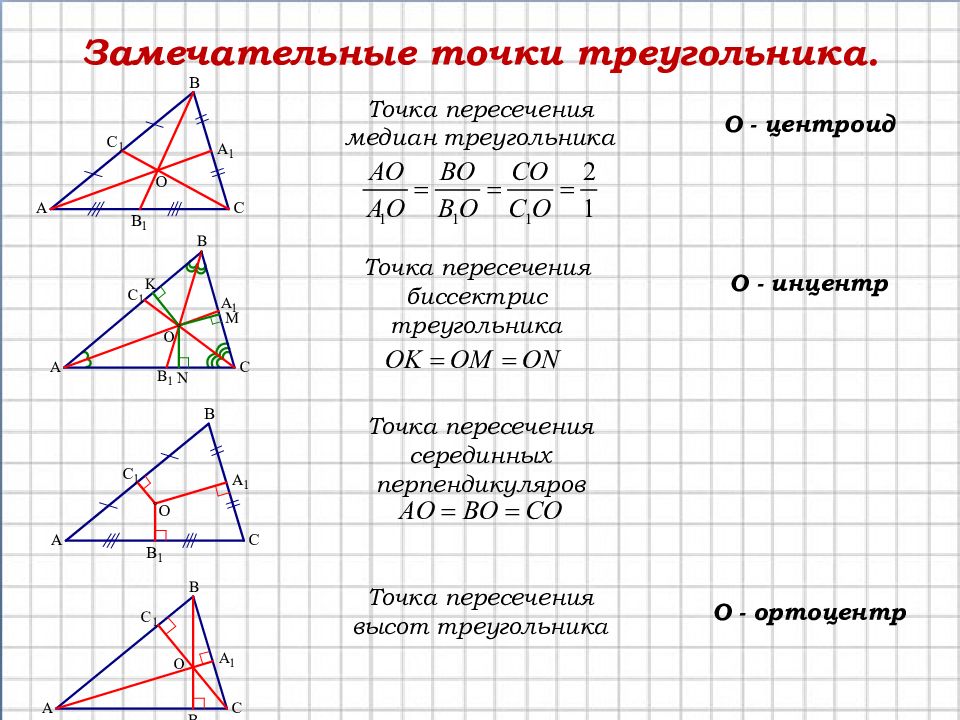
Если треугольник является прямоугольным, медианы также могут быть использованы для определения координат гипотенузы и других сторон.
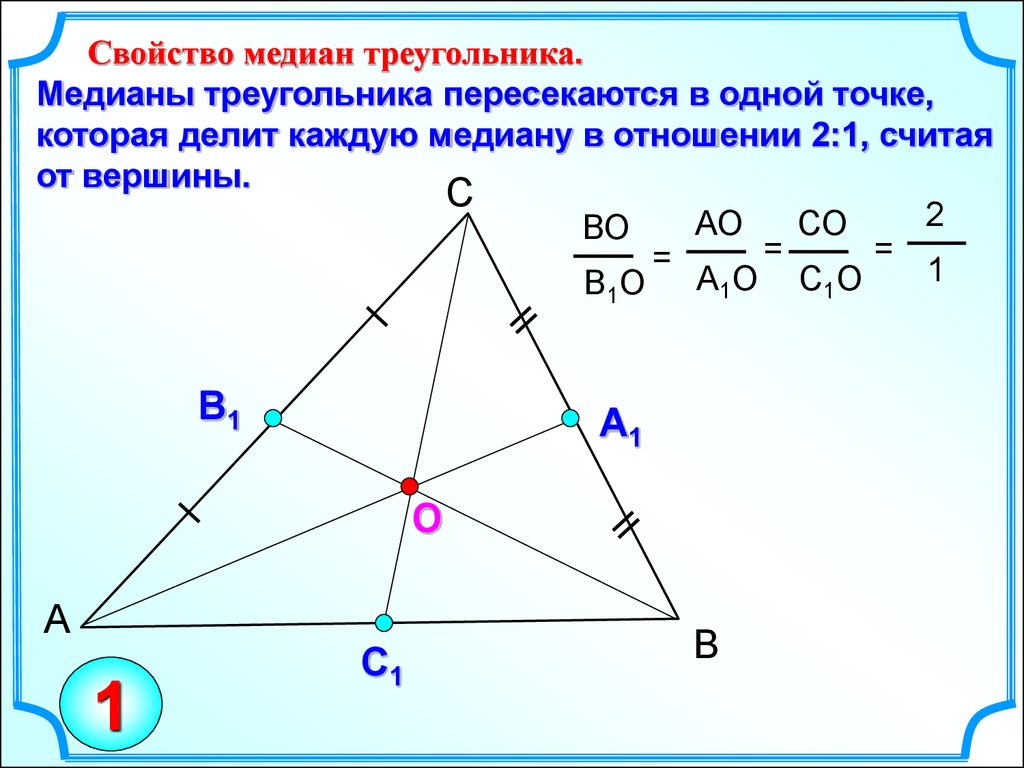

При решении задач на нахождение расстояний от центра масс до вершин треугольника, медианы помогают упростить вычисления.


8. Медиана треугольника и её свойства.