Как эффективно использовать соотношения в прямоугольных треугольниках для решения задач и вычислений

На этой странице вы найдете ключевые формулы и полезные советы по решению задач с прямоугольными треугольниками. Мы подробно рассмотрим основные соотношения и принципы, которые помогут вам легко справляться с такими задачами в геометрии. Применяйте эти советы и улучшайте свои знания!

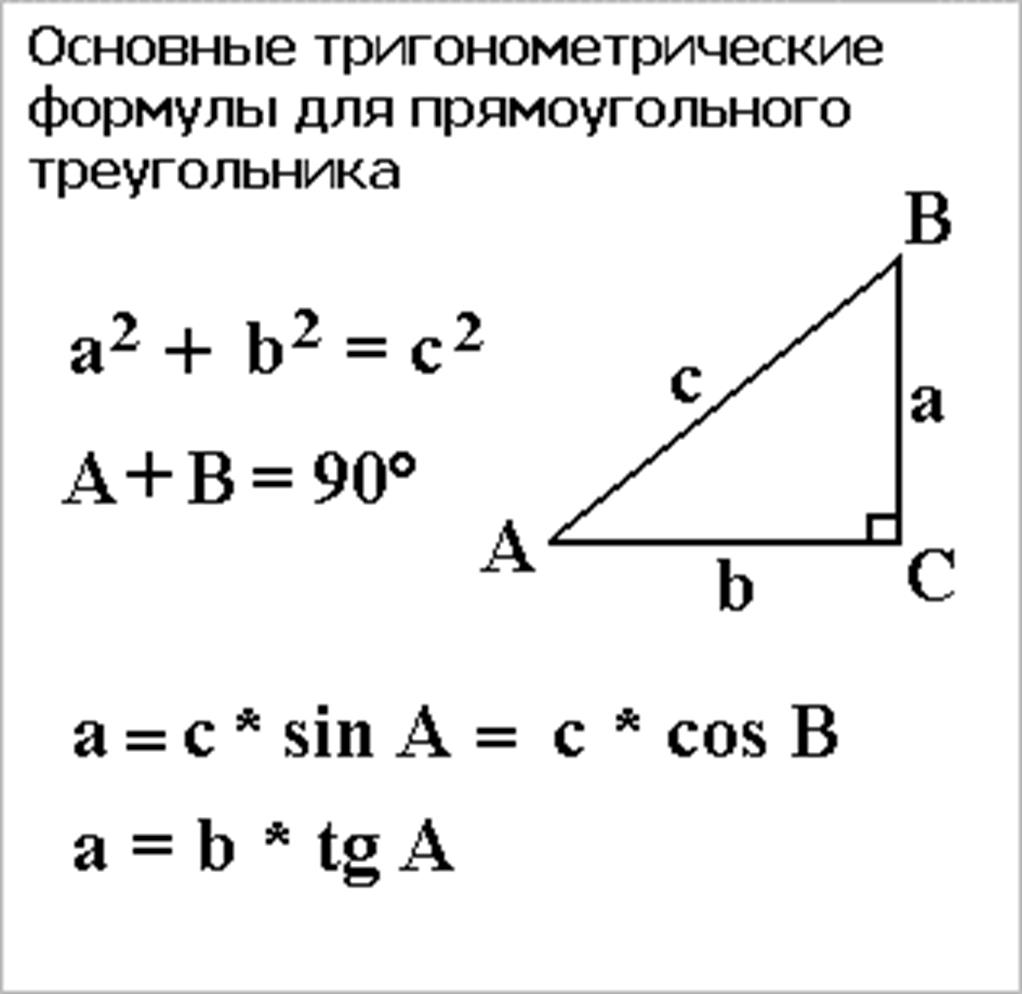
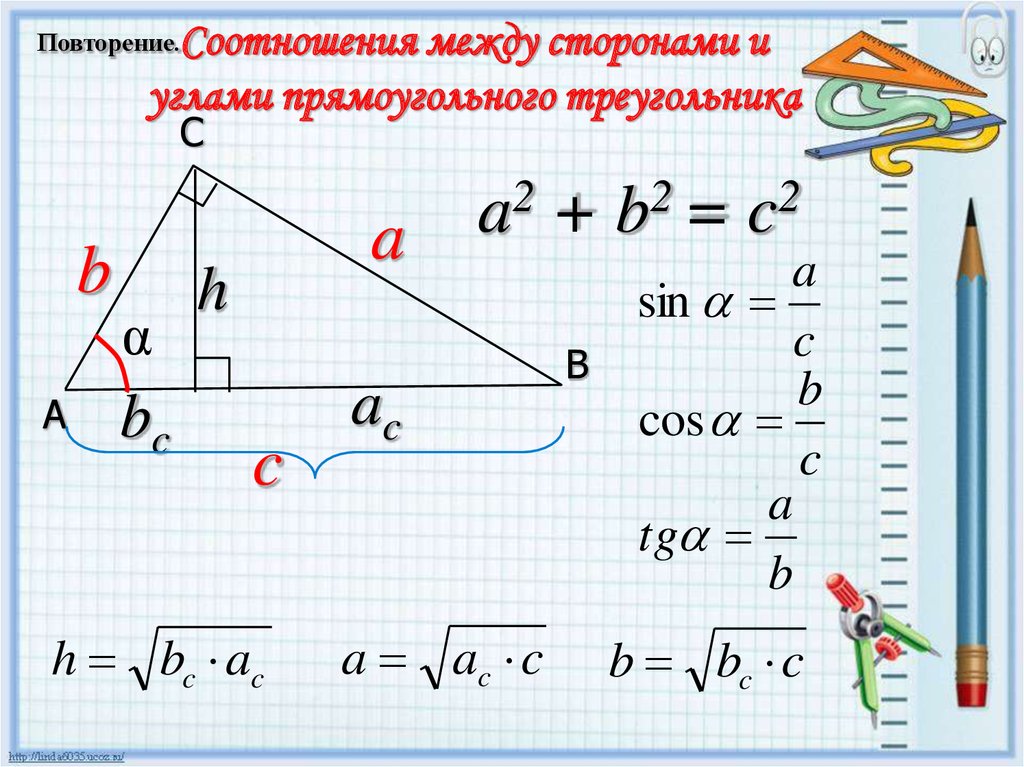
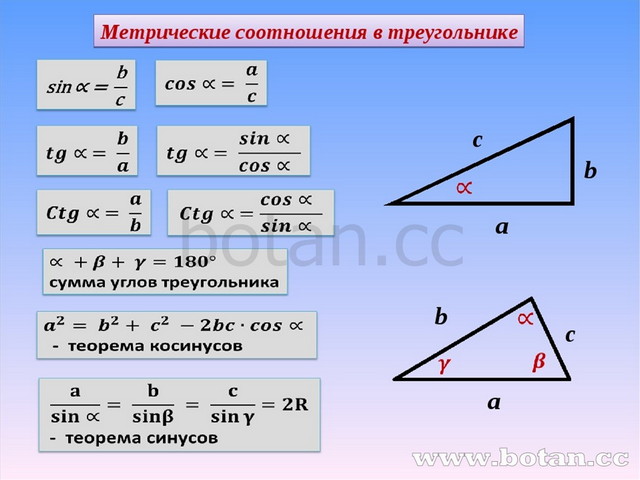
Не забывайте, что гипотенуза всегда противолежит прямому углу и является самой длинной стороной треугольника.

Используйте теорему Пифагора для нахождения неизвестной стороны прямоугольного треугольника: c² = a² + b².

Для вычисления углов в прямоугольном треугольнике используйте тригонометрические функции: синус, косинус и тангенс.

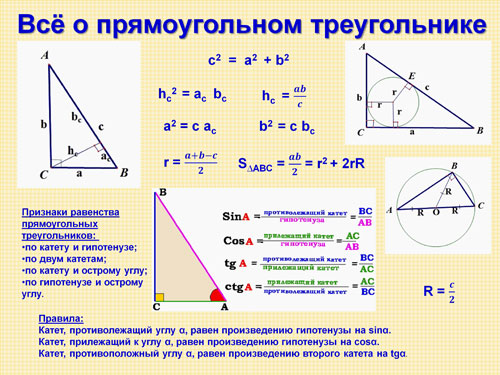
Если вам нужно найти катет, применяйте формулы: a = c * sin(α) или b = c * cos(α), где α — угол в треугольнике.

Для нахождения угла используйте аркфункции: α = arcsin(a/c), β = arccos(b/c), где a и b — катеты, а c — гипотенуза.

При решении задач на прямоугольные треугольники всегда проверяйте правильность вычислений с помощью теоремы Пифагора.

Запоминайте, что отношение катетов и гипотенузы в прямоугольном треугольнике дает вам значение синуса и косинуса.

Используйте квадратные корни для вычислений, чтобы точно найти длины сторон, если вы используете теорему Пифагора.

Помните, что сумма углов в прямоугольном треугольнике всегда равна 180 градусам, из которых один угол — прямой.

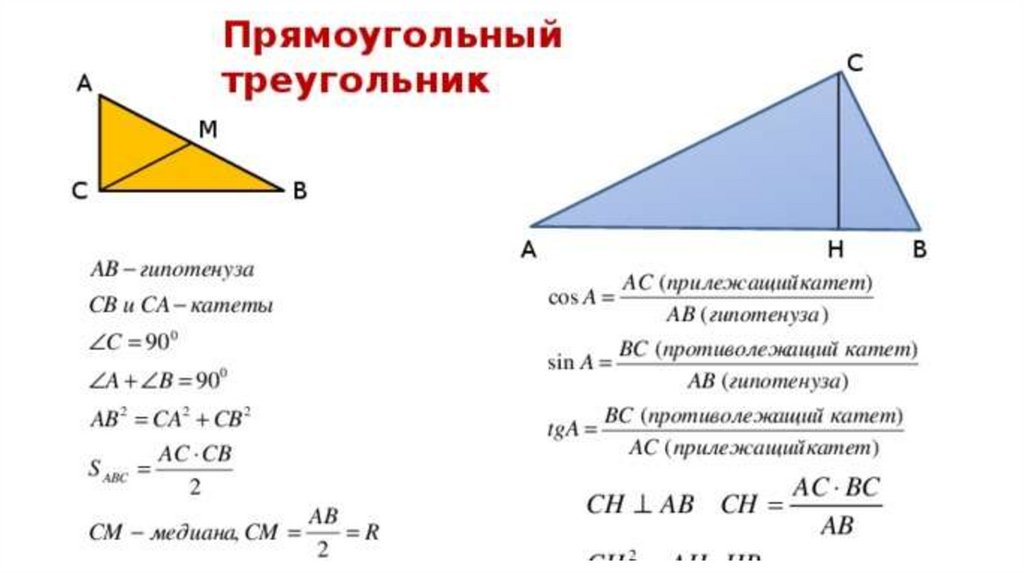
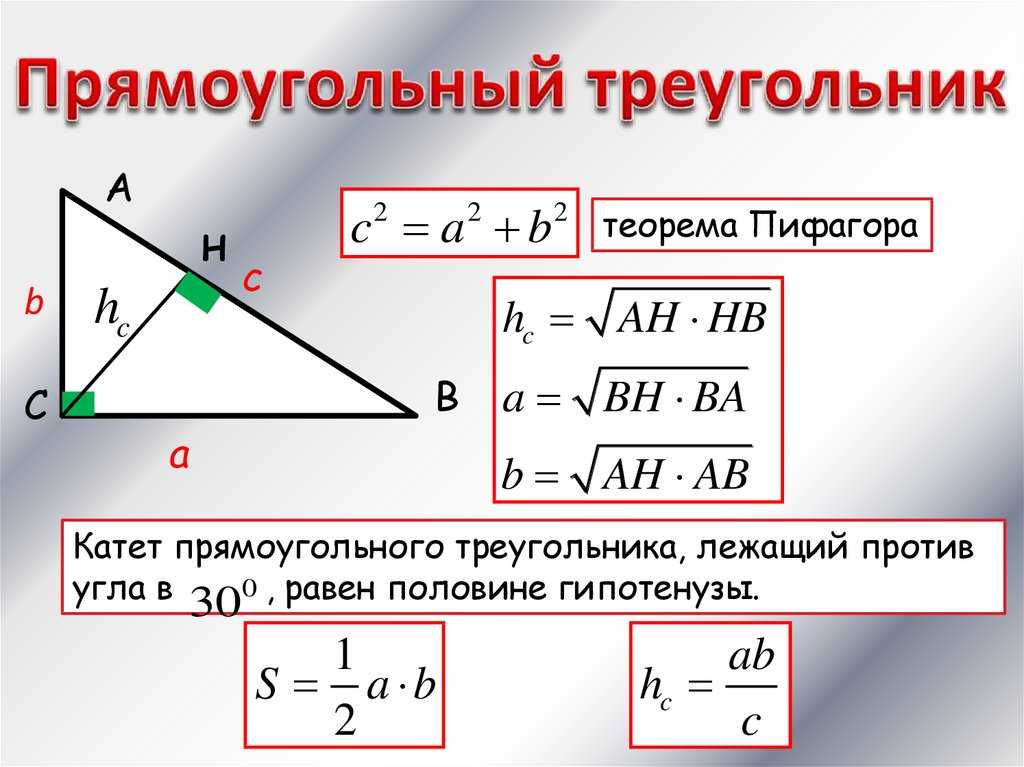
Для ускорения расчетов используйте калькулятор или специальные онлайн-инструменты для работы с тригонометрическими функциями.