Визуальное сравнение синуса и косинуса с помощью диаграммы Венна
На этой странице представлено детальное объяснение различий и сходств между функциями синуса и косинуса, проиллюстрированное с помощью диаграммы Венна. Этот подход помогает наглядно понять, как эти функции соотносятся друг с другом и где пересекаются их свойства. Также приводятся полезные советы по запоминанию и использованию этих тригонометрических функций.

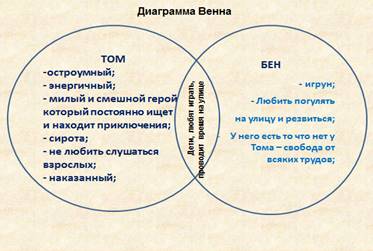
Помните, что синус и косинус имеют одинаковые значения при углах 0° и 180°, но различаются в других точках.

Сравнение значений тригонометрических выражений
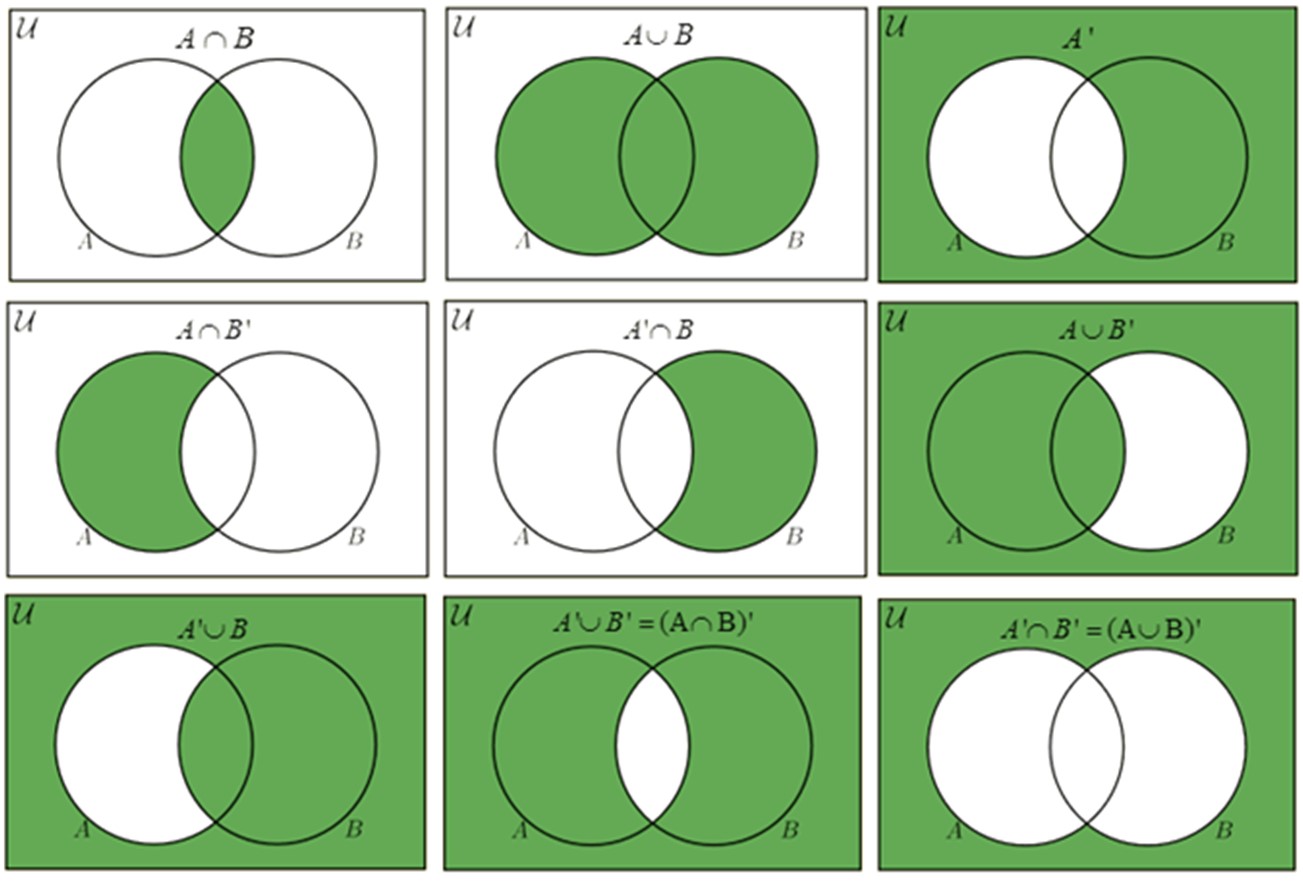
Чтобы понять пересечения синуса и косинуса, посмотрите на диаграмму Венна: общие области — это точки их равенства.

Сравнение значений косинусов разных углов

Для запоминания различий используйте ассоциации: синус — это отношение противолежащего катета к гипотенузе, а косинус — прилежащего катета.
Как построить графики синуса и косинуса в Excel. Эксель для начинающих

Когда оба значения (синус и косинус) равны нулю, это происходит в точках углов 0°, 180° и 360°.

Теорема синусов и теорема косинусов
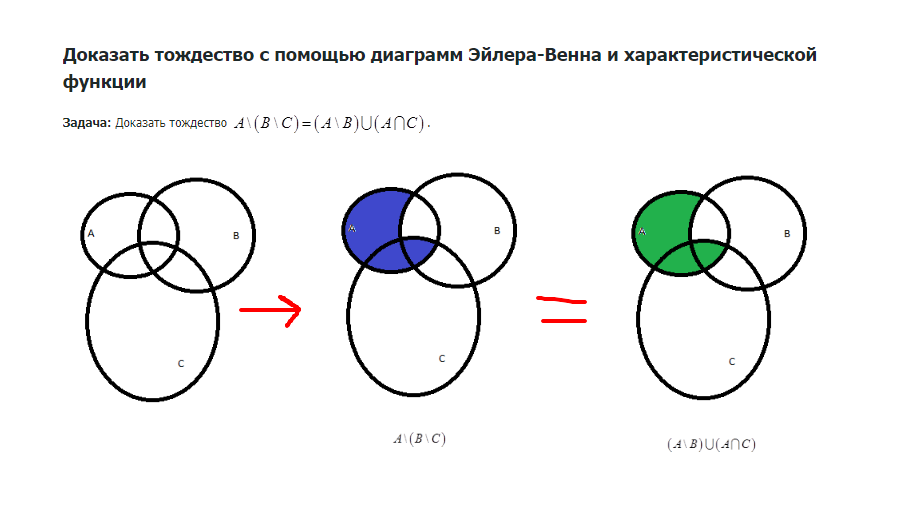
Диаграмма Венна отлично иллюстрирует, где синус и косинус одинаковы, а где — различаются.

Синус, косинус и тангенс Решение задач по геометрии
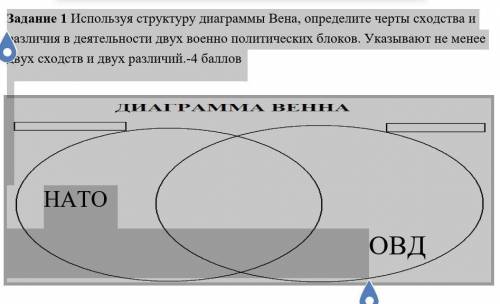
Синус и косинус — это периодические функции, и их значения повторяются с периодом 360°.

Зачем нужны синусы и косинусы?
Обратите внимание, что синус и косинус никогда не могут одновременно быть равны единице или минус единице для одного и того же угла.

Сравнение значений синусов разных углов


Диаграмма Венна помогает наглядно различать их особенности, такие как синус для углов от 0° до 90° и косинус для углов от 90° до 180°.
Для углов в 90° и 270° синус равен ±1, а косинус — 0, что также важно для понимания различий.

Использование диаграмм и графиков в изучении тригонометрии помогает лучше визуализировать связь и отличие между синусом и косинусом.