Как использовать шаблоны функции y = x² в алгебре для решения задач
Шаблон функции y = x² является основой многих математических задач в алгебре. Он помогает понять, как работает квадратичная зависимость, и научиться строить графики, а также решать различные уравнения и неравенства. В этой подборке вы найдете полезные советы и примеры применения данной функции в различных задачах.
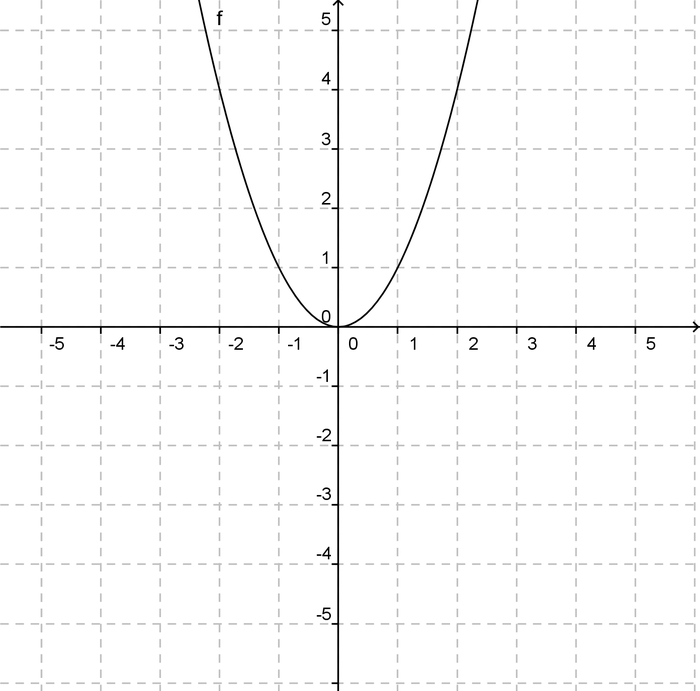

Для построения графика функции y = x² запомните, что его форма всегда будет параболой, направленной вверх.

Функция у=х² и у=х³ и их графики. Алгебра, 7 класс


Для более точного построения графика функции начните с нахождения её вершины, которая всегда будет в точке (0, 0).
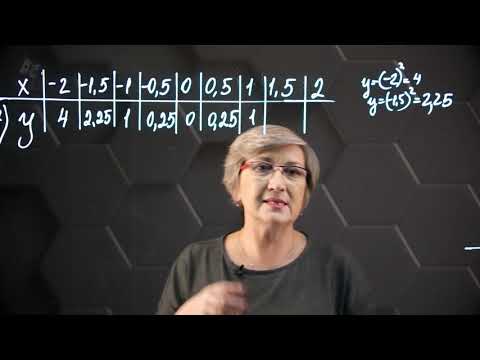
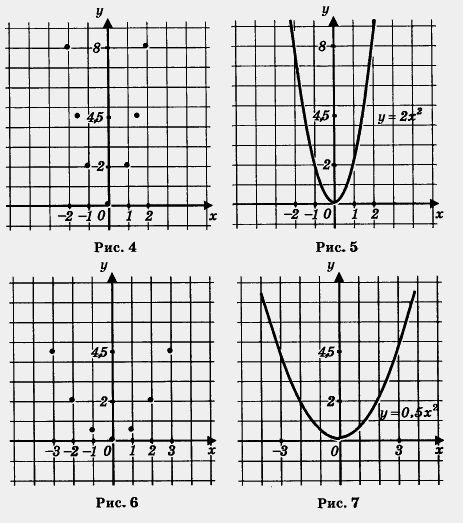
График функции y=x² (y=аx).
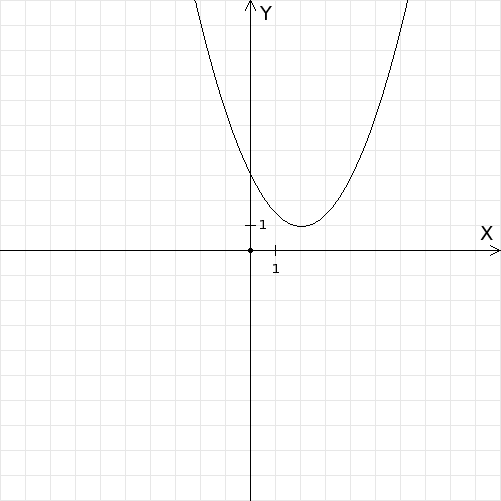
Запоминайте, что если к функции добавляется константа, например y = x² + 2, то график сдвигается на 2 единицы вверх.

Всё о квадратичной функции. Парабола - Математика TutorOnline
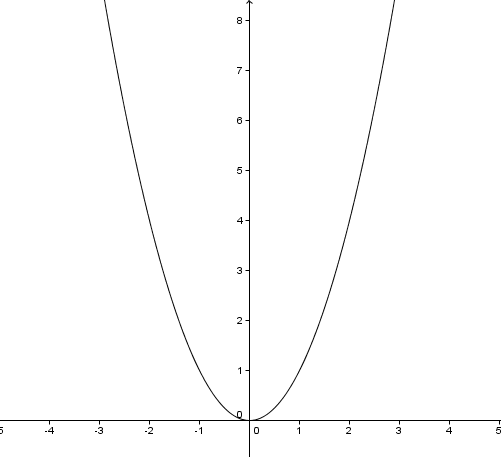
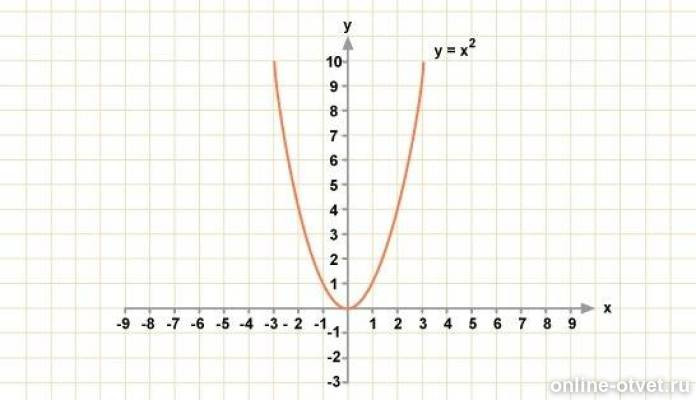
Для нахождения корней функции y = x² = 0 решайте уравнение x² = 0, что дает единственный корень x = 0.

Графики функций y=ax²+n и y=a(x-m)². Алгебра, 9 класс
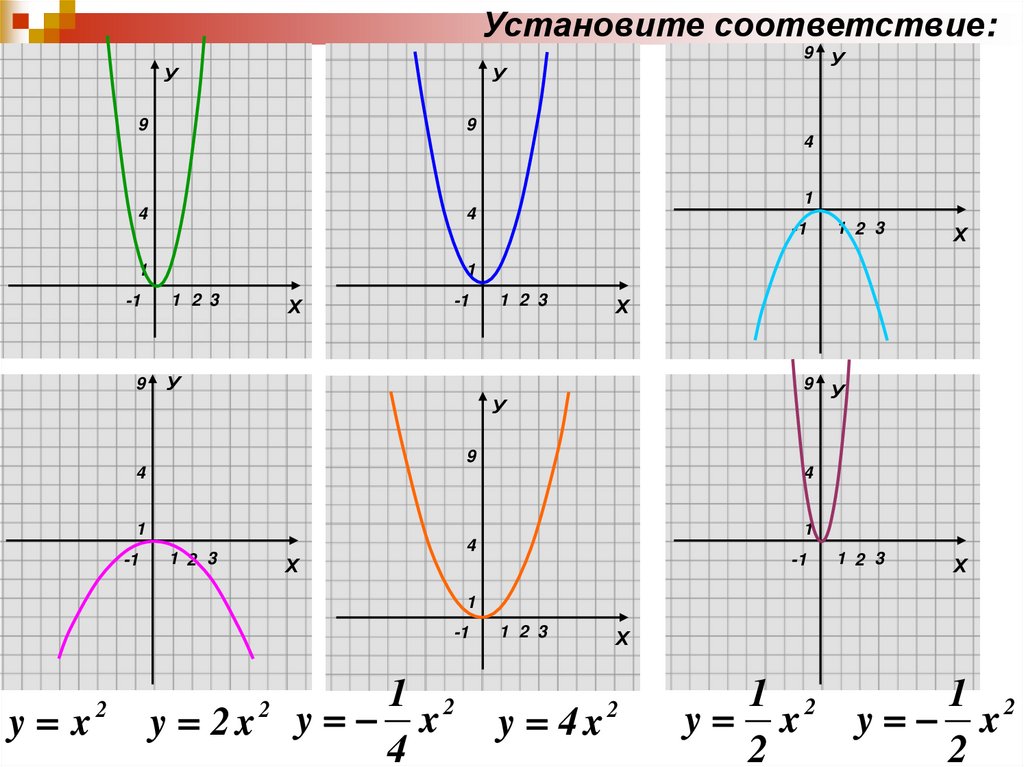
При анализе функции y = x² всегда учитывайте её симметричность относительно оси Y.

Квадратичная функция за 5 минут

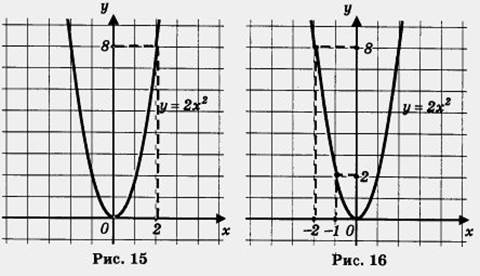
Если перед x² стоит коэффициент, например y = 2x², это растягивает график вдоль оси Y.
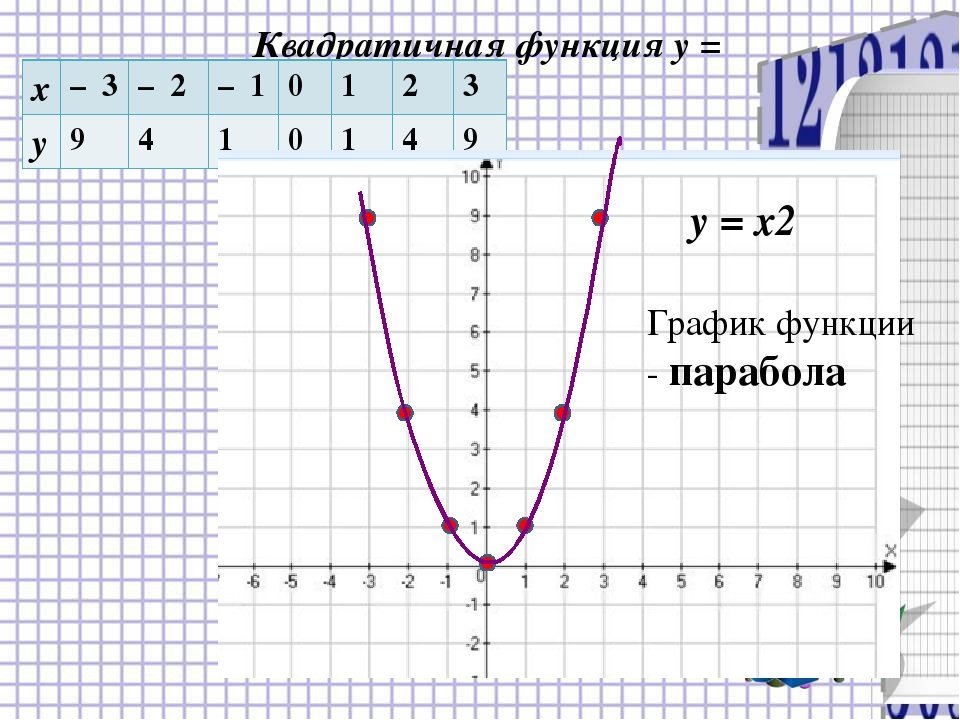
Для вычисления значений функции для различных x используйте формулу y = x², подставляя нужные значения x.

А8 Шаблон параболы
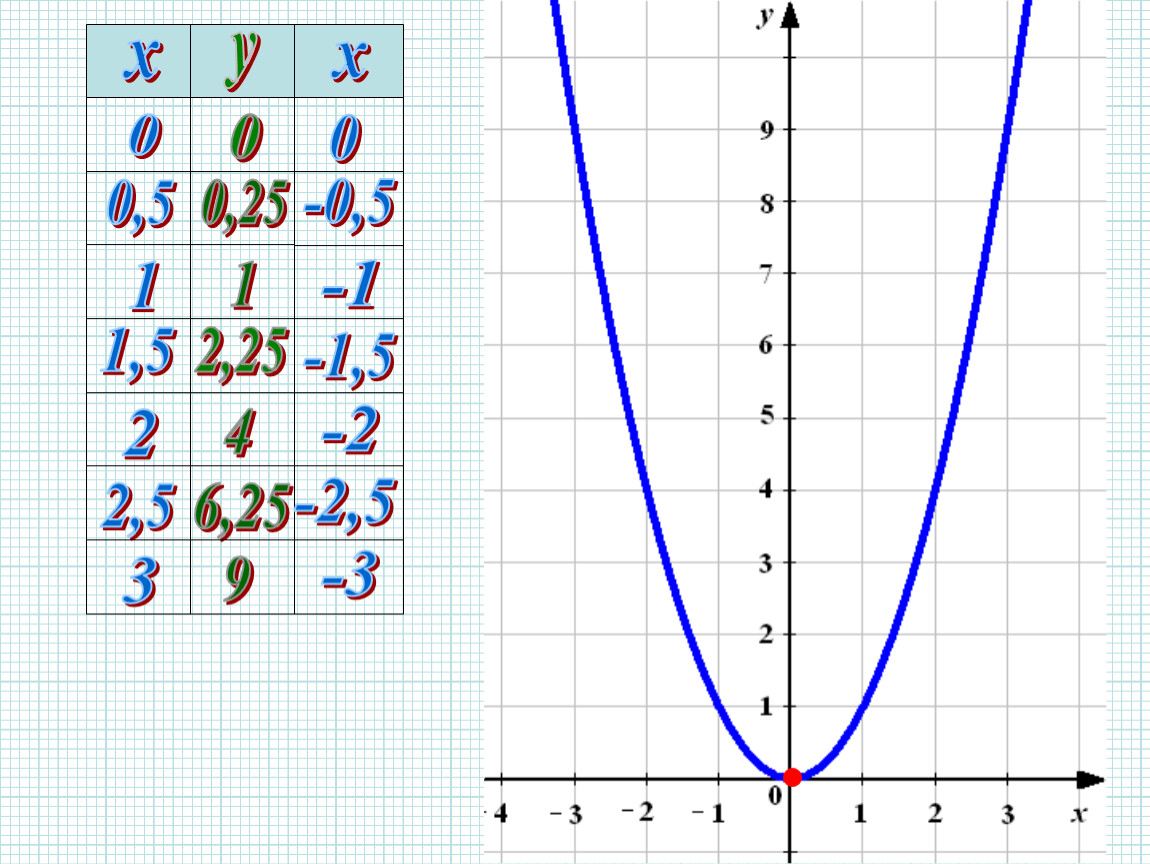
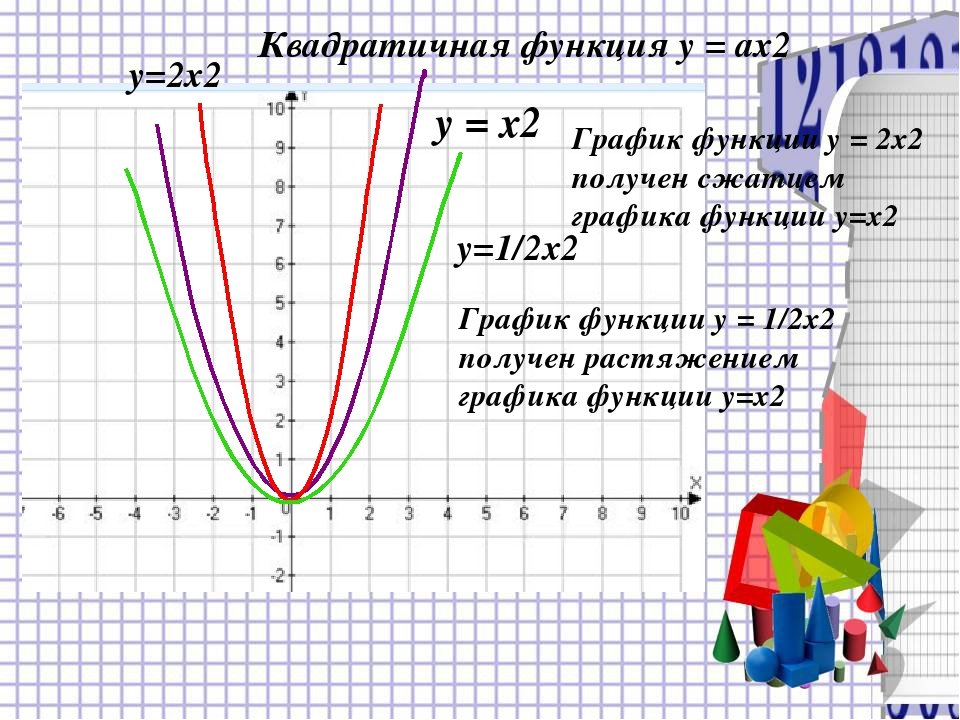
График функции y = x² всегда будет проходить через точку (0, 0), так как значение функции в этой точке равно 0.
Функция y=x2 и её график – 8 класс алгебра
Если в функции есть знак минус, например y = -x², то график будет направлен вниз, создавая параболу, обращённую вниз.
Построение графиков функций с помощью шаблона

Для более сложных функций, например y = a(x - h)² + k, важно учитывать сдвиг графика и его растяжение в зависимости от значений a, h и k.

