Как рассчитать и визуализировать сечение правильной треугольной призмы: подробное руководство
На этой странице представлены фотографии и советы по правильному пониманию и расчету сечений правильной треугольной призмы. Мы объясняем, как можно точно визуализировать различные виды сечений, их геометрические особенности и практическое применение в различных областях науки и техники.
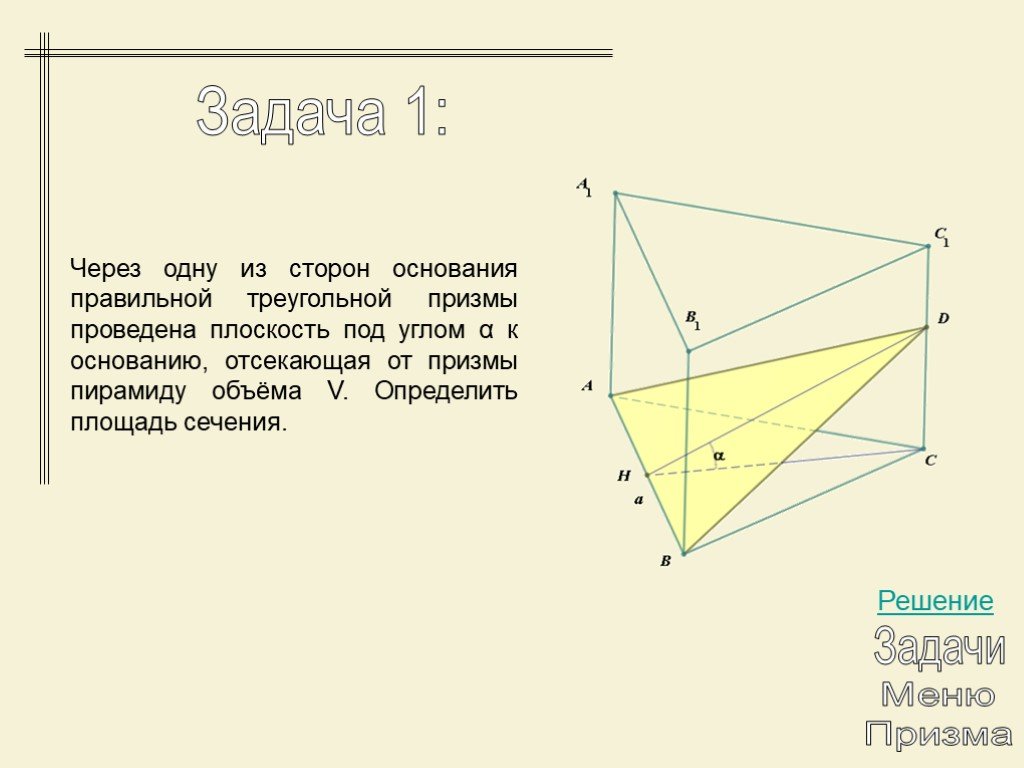

Для точного понимания сечений правильной треугольной призмы важно помнить, что сечение всегда будет параллельно одной из граней основания.

Как строить сечения тетраэдра и пирамиды

При сечении правильной треугольной призмы плоскостью, проходящей через ее центр, результат будет равносторонним треугольником.

ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИ
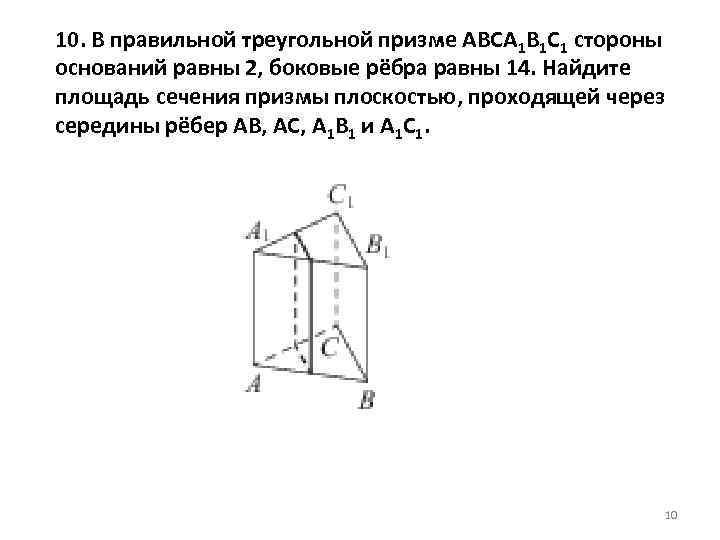
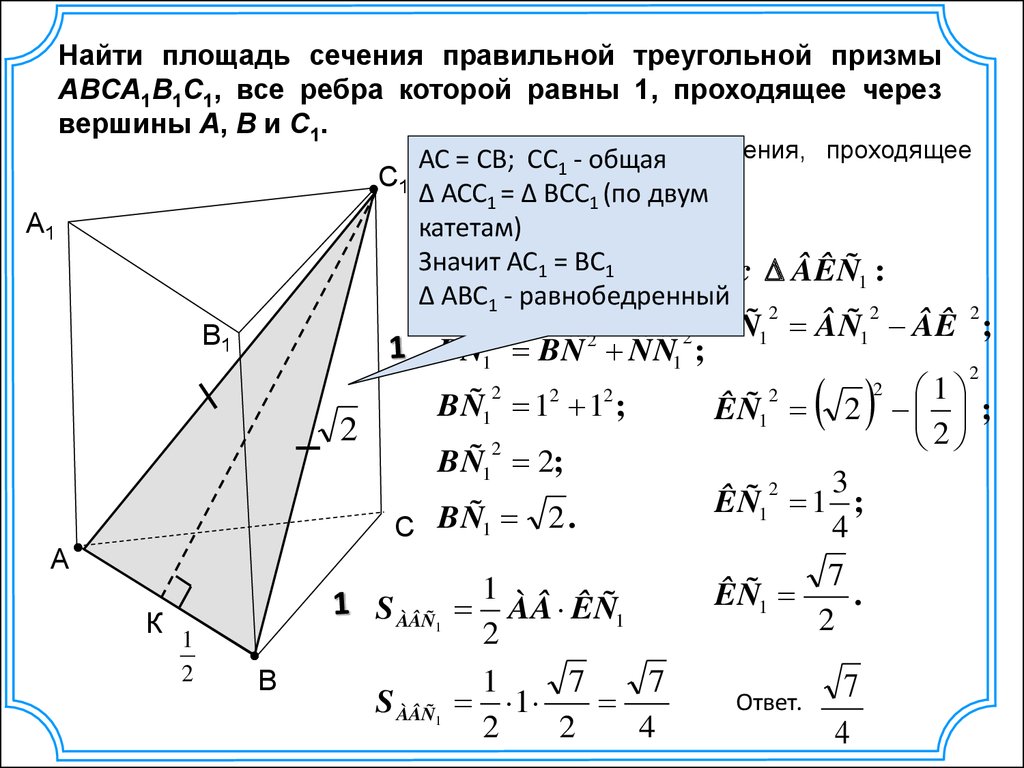
Для более сложных сечений полезно использовать 3D-моделирование, что поможет наглядно увидеть изменения формы сечения в зависимости от положения плоскости.

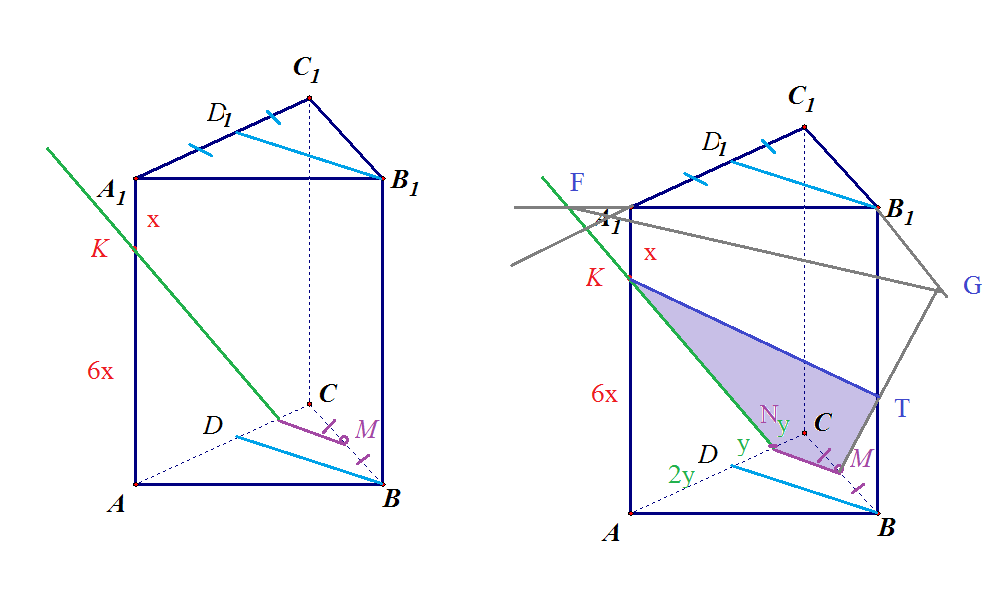
Задача 2.1 Сечение треугольной призмы
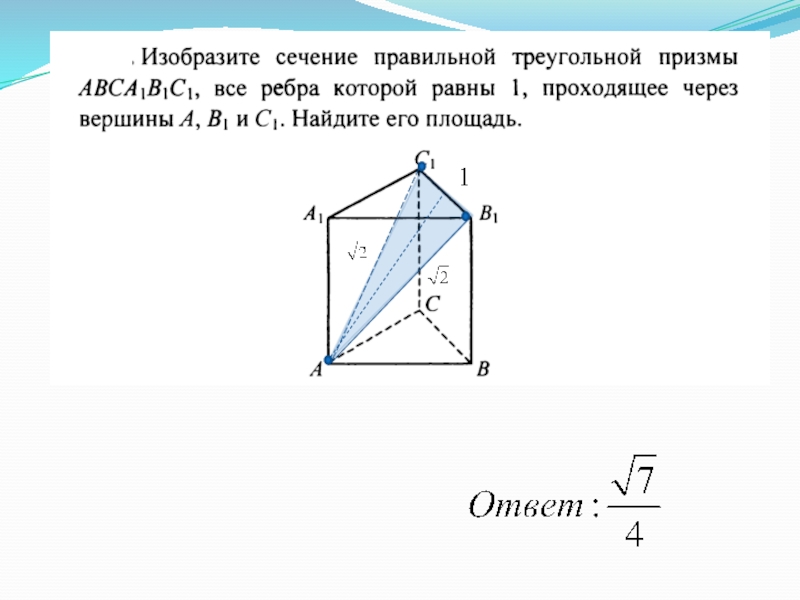

При рассмотрении сечений через вершины правильной треугольной призмы можно получить различные геометрические фигуры, в том числе трапеции и прямоугольники.
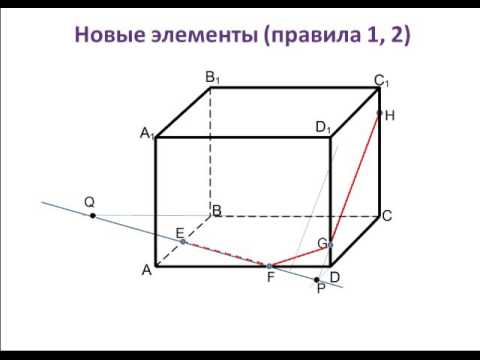
Сечение призмы плоскостью, заданной тремя точками
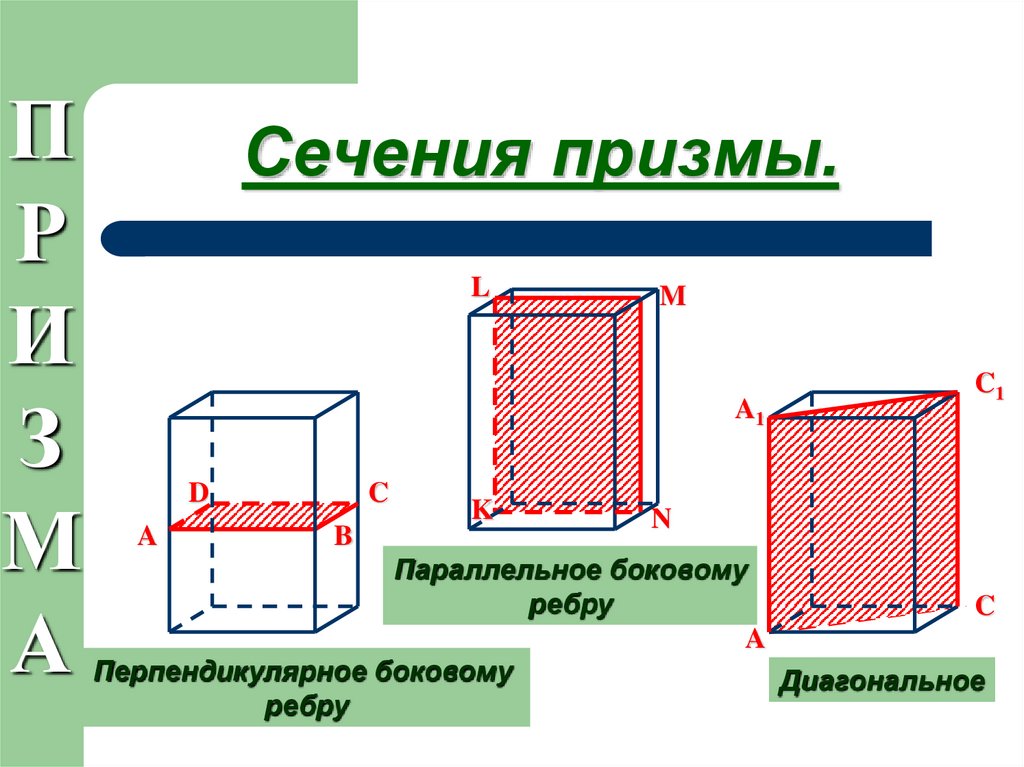
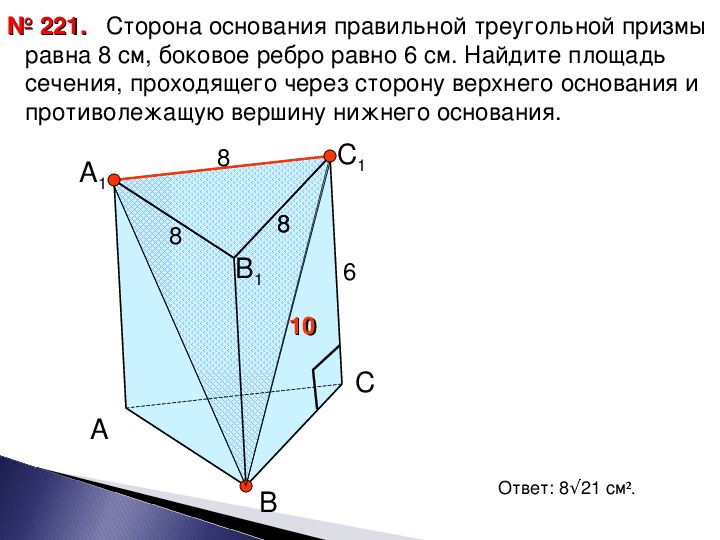
Важно учитывать, что для правильных и симметричных сечений угол наклона плоскости относительно оси призмы играет ключевую роль в определении конечной формы.

Правильная треугольная призма

Изучая сечения треугольной призмы, стоит поэкспериментировать с разными углами наклона плоскости, чтобы лучше понять, как форма сечения изменяется при разных пересечениях.

8 задание ЕГЭ математика профиль.В сосуд, имеющий форму правильной треугольной призмы, налили 2300
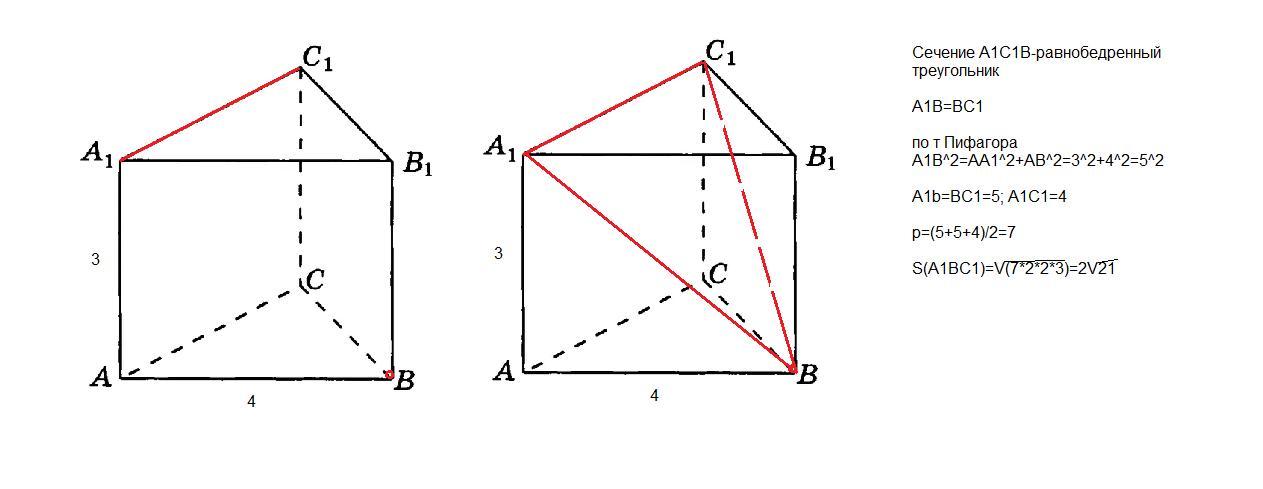
Для учебных целей полезно использовать простые геометрические фигуры для представления сечений и научиться визуализировать их в двумерной и трехмерной проекциях.
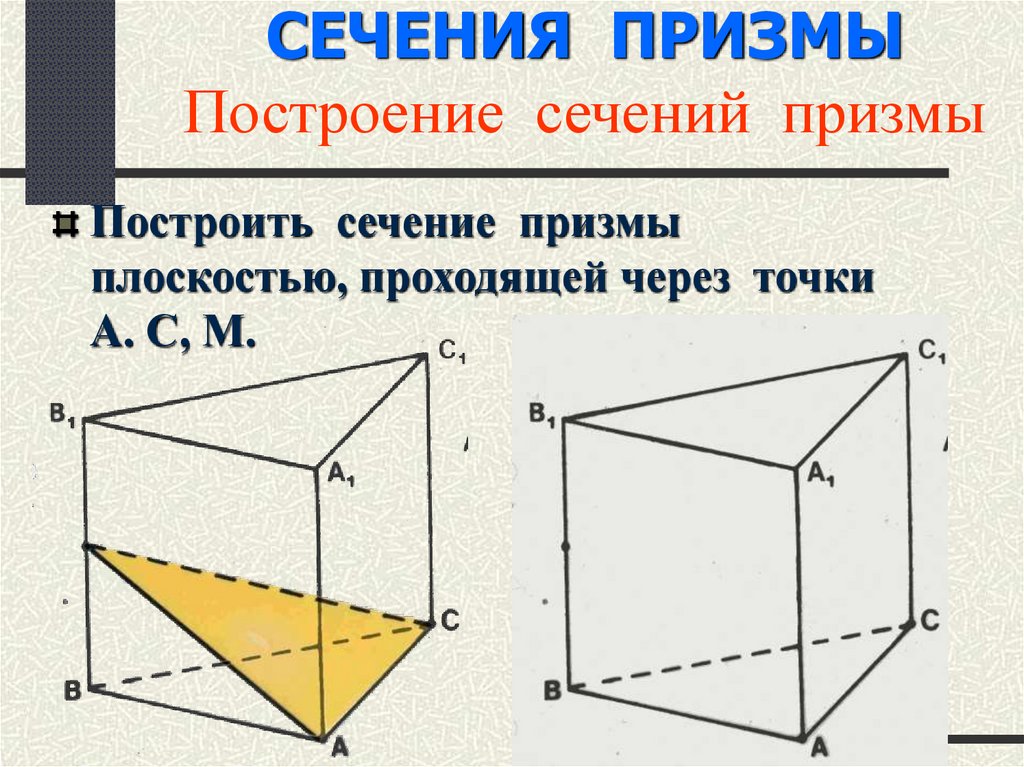
Когда вы работаете с физическими моделями, такие как пластмассовые или деревянные модели, можно получить точное представление о том, как сечение меняется при различных углах разреза.
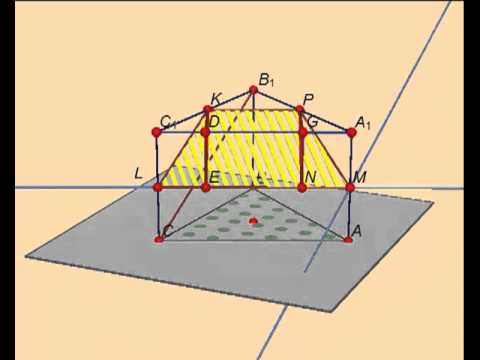
Сечение правильной треугольной призмы. Найти объём части призмы
Рекомендуется также изучить аналогичные сечения других многогранников, чтобы лучше понять закономерности изменения форм в зависимости от геометрии объекта.
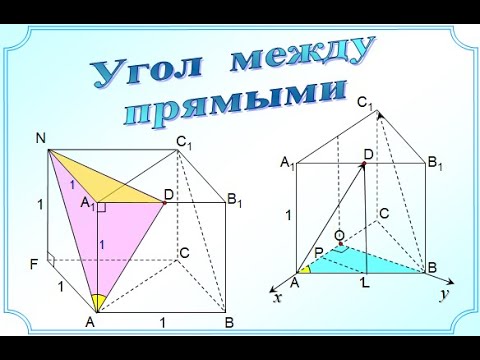
Угол между прямыми Треугольная призма
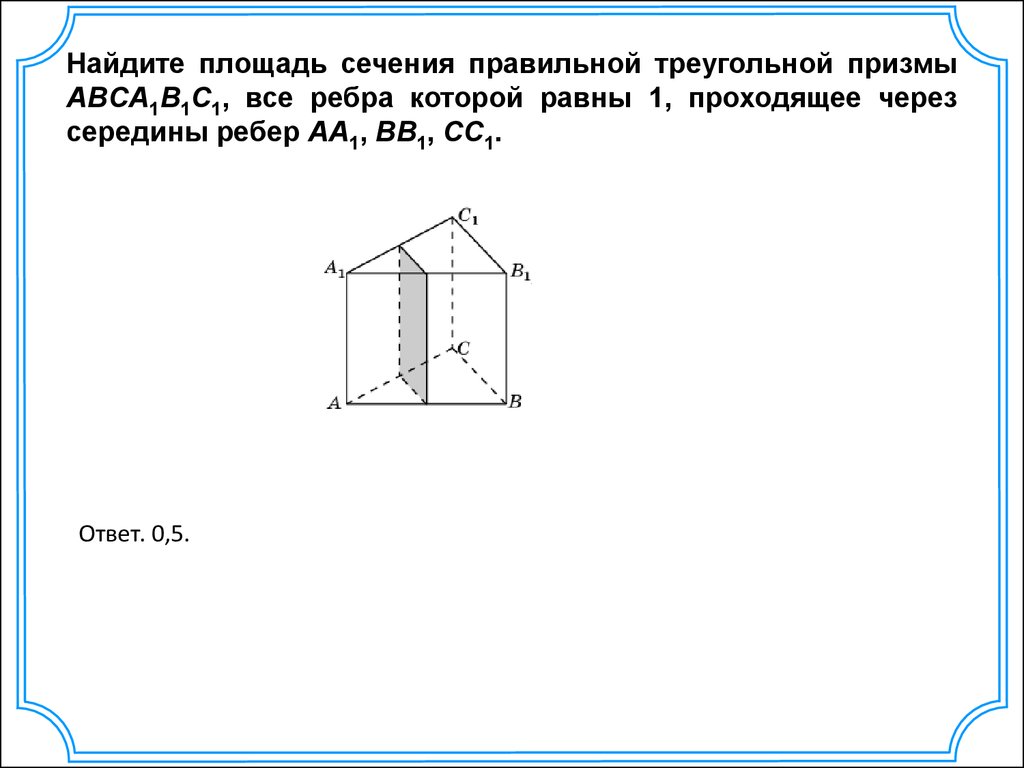
Не забывайте о методах проекций, таких как аксонометрия, которые помогают наглядно изображать сложные сечения и трехмерные формы для лучшего их восприятия.
Как строить сечения