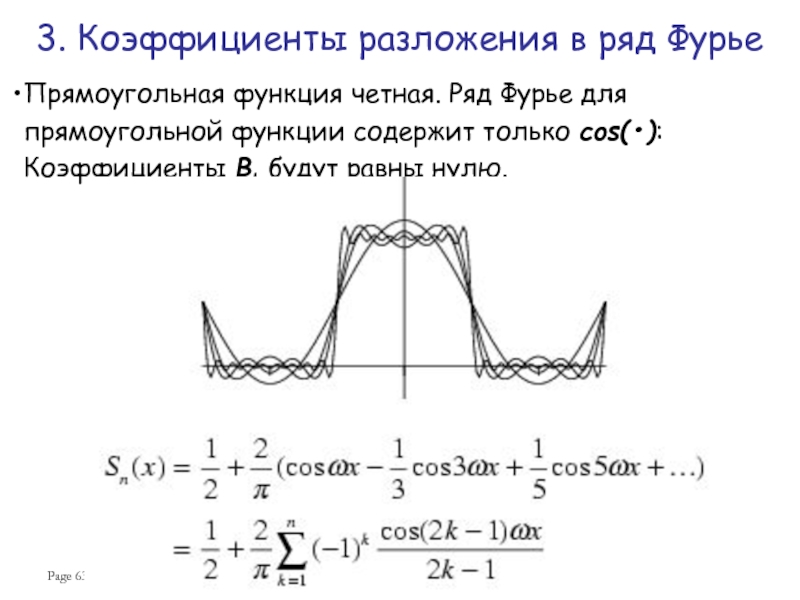
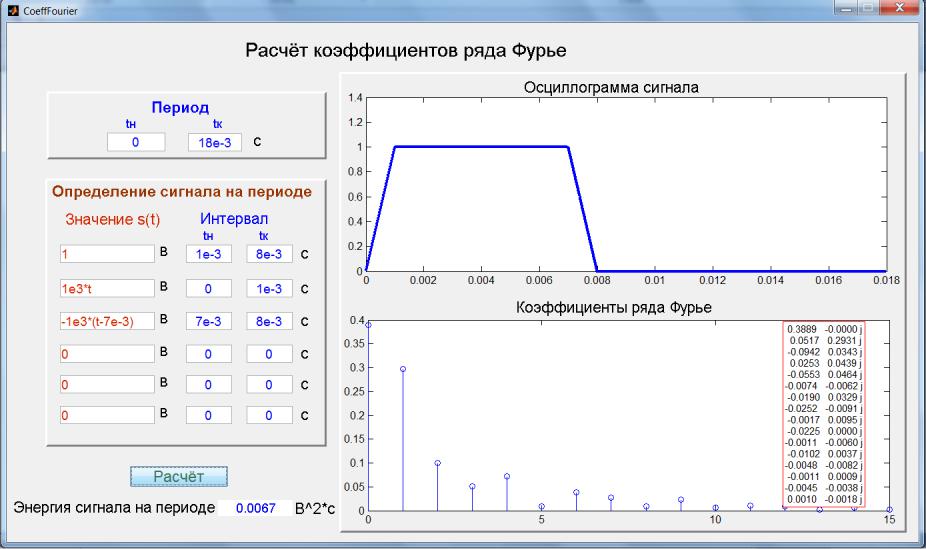
Как использовать коэффициенты Фурье для эффективного анализа различных сигналов
В этой статье мы подробно рассматриваем ряд Фурье и его ключевое значение в математическом анализе и обработке сигналов. Вы узнаете, как разложение функции на коэффициенты Фурье помогает анализировать различные виды данных и применять это знание на практике. Смотрите примеры, которые помогут вам лучше понять, как использовать этот мощный инструмент в реальных задачах.



Для точного применения ряда Фурье важно понимать, как работают его основные принципы, включая разложение функции на гармоники.

Откуда взялся и что такое Ряд Фурье? Упрощенный вывод коэффициентов ряда

Рекомендуется практиковаться на простых примерах перед применением ряда Фурье в сложных расчетах, чтобы развить интуитивное понимание процесса.
06. Ряды Фурье

Используйте преобразование Фурье для анализа периодических сигналов, таких как звуковые волны или колебания, что значительно улучшит результаты ваших исследований.
Быстрое преобразование Фурье (БПФ/FFT) в осциллографе: миф или реальность?


Обратите внимание на скорость сходимости ряда Фурье для разных типов функций, чтобы оптимизировать вычислительные процессы.
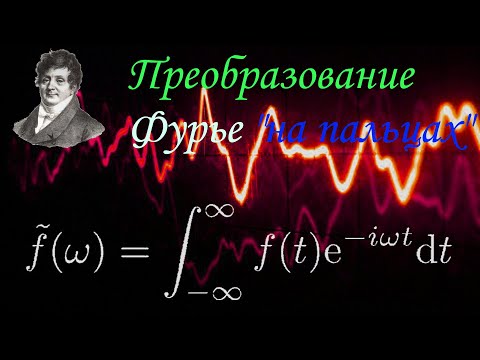
AGalilov: Преобразование Фурье \


При анализе сигналов с шумами стоит использовать усреднение и фильтрацию для получения более точных коэффициентов Фурье.

Что такое ГАРМОНИКА
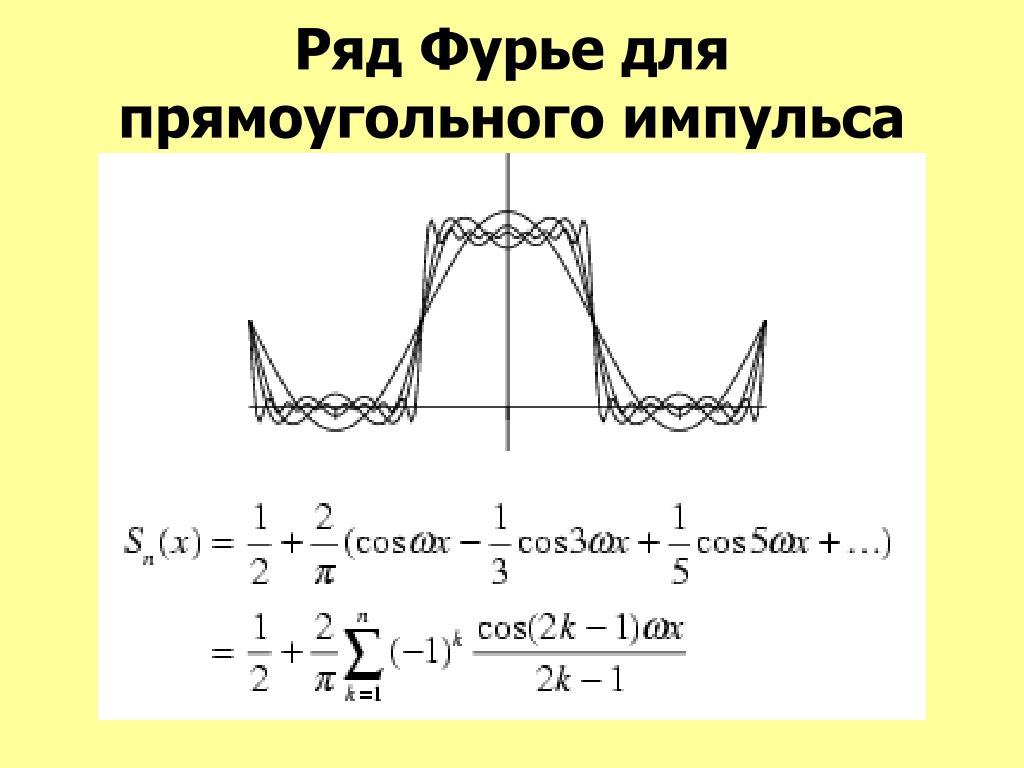
Для работы с реальными сигналами часто необходимо использовать дискретное преобразование Фурье (ДПФ), которое подходит для численных вычислений.

Обязательно учитывайте особенности оконных функций при работе с временными рядами, чтобы минимизировать искажения, возникающие при анализе сигналов.
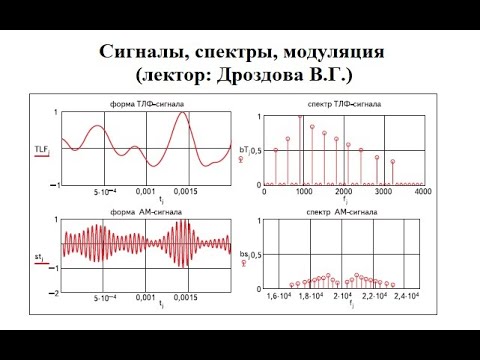
Частотное и временное представление сигналов. Спектр. Модуляция

Не забывайте проверять корректность реконструкции исходных данных после разложения на коэффициенты Фурье, чтобы избежать ошибок в интерпретации.

13.2 Разложение функции в ряд Фурье. Пример 1.
Что такое Спектр напряжения, Гармоники, Преобразование Фурье, FFT, THD - это просто!
Изучите различные алгоритмы вычисления коэффициентов Фурье, такие как быстрые преобразования Фурье (БПФ), которые существенно ускоряют вычисления.

Применяйте ряд Фурье в различных областях науки, от анализа биологических сигналов до обработки изображений, чтобы расширить спектр возможностей анализа данных.

13.1. Что такое ряд Фурье?