Радиус-вектор движения по окружности: что важно знать для правильных расчетов

Радиус-вектор, описывающий движение по окружности, является важным элементом в механике и математике. Этот вектор характеризует положение объекта на круговой траектории, а его правильное понимание позволяет эффективно решать задачи, связанные с движением по кругу, используя соответствующие физические и математические формулы. В этой статье мы собрали полезные советы для лучшего усвоения материала и практических расчетов.

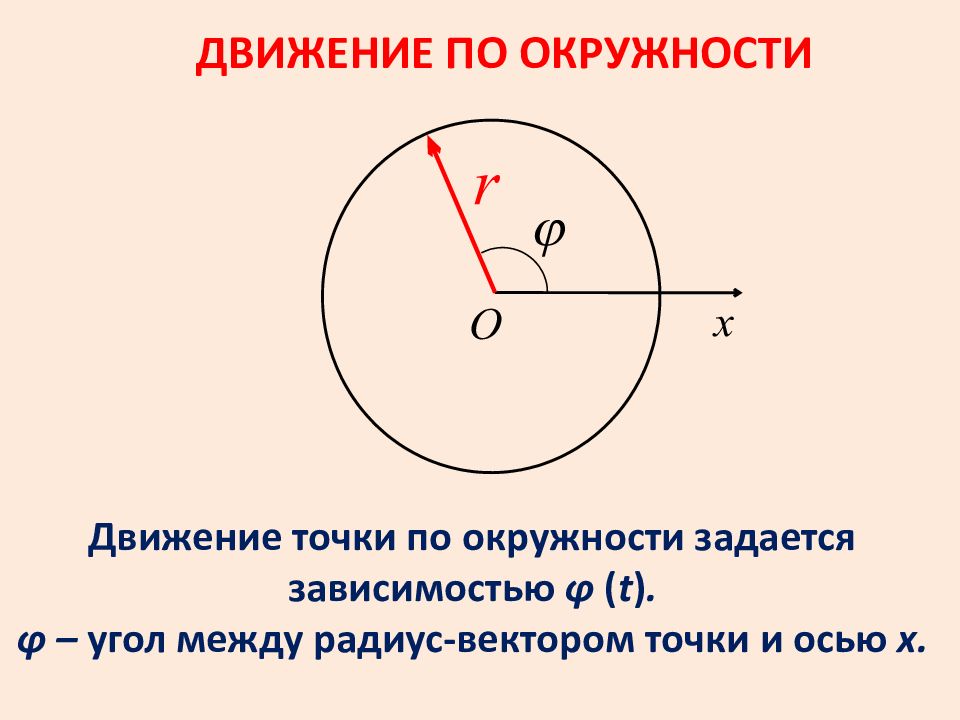
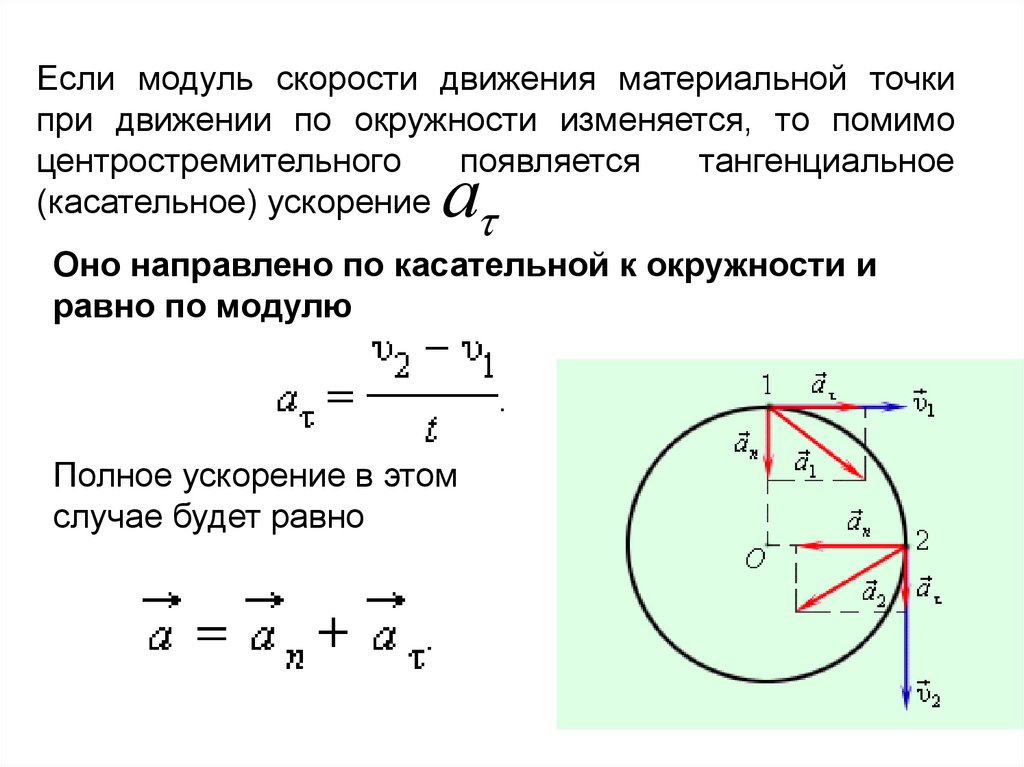
Обратите внимание на то, что радиус-вектор всегда направлен от центра окружности к точке на траектории движения.

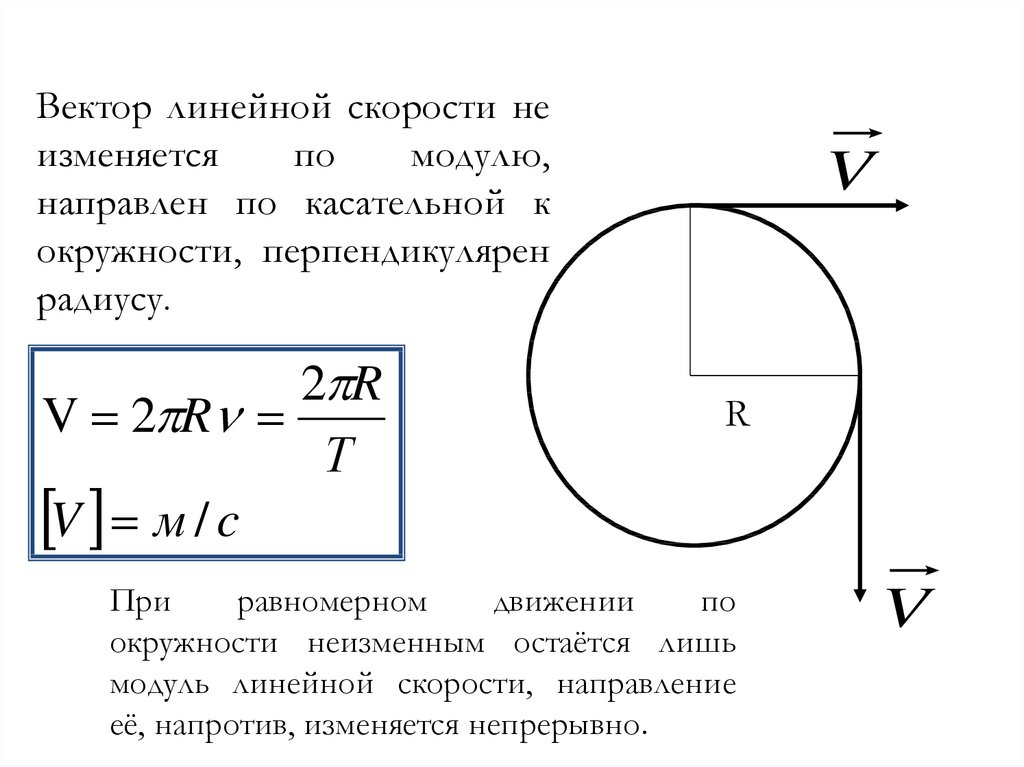
При движении по окружности радиус-вектор изменяет свое направление, но его длина остаётся постоянной и равной радиусу окружности.

Если вам нужно вычислить компоненты радиус-вектора, используйте декартовы координаты для упрощения расчетов.

Не забывайте, что радиус-вектор векторен и может быть выражен через его проекции на оси X и Y.

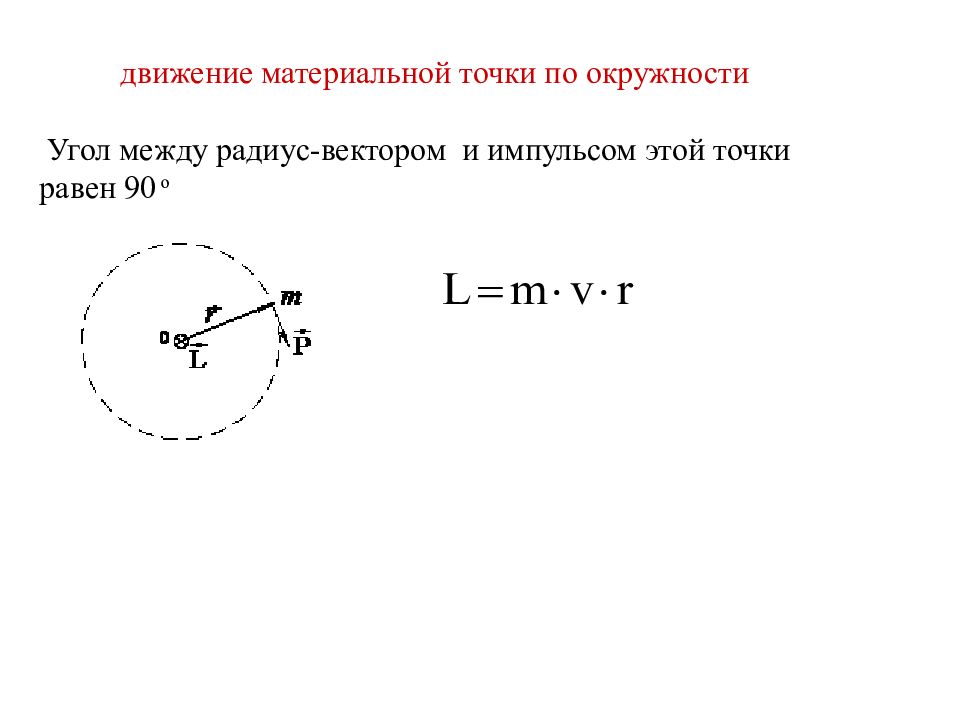
Для сложных задач с движением по окружности полезно использовать угловые величины, такие как угловая скорость и угол поворота.

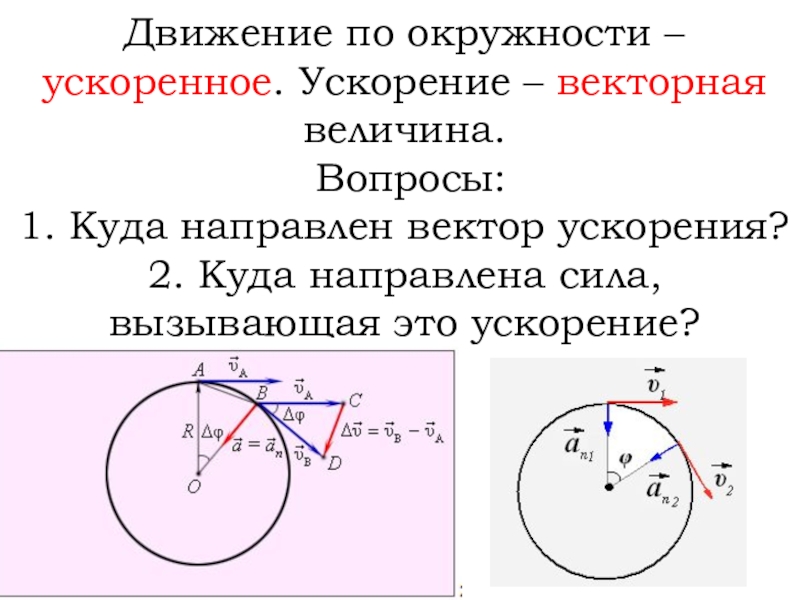
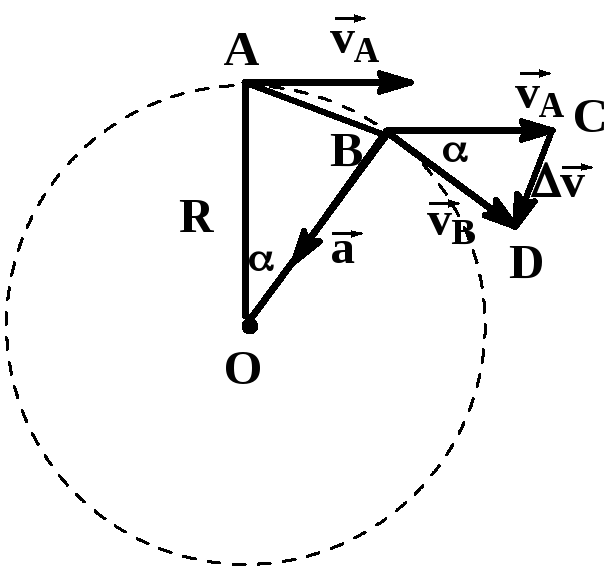
Не забывайте про зависимость между линейной и угловой скоростью при расчете скорости объекта на окружности.

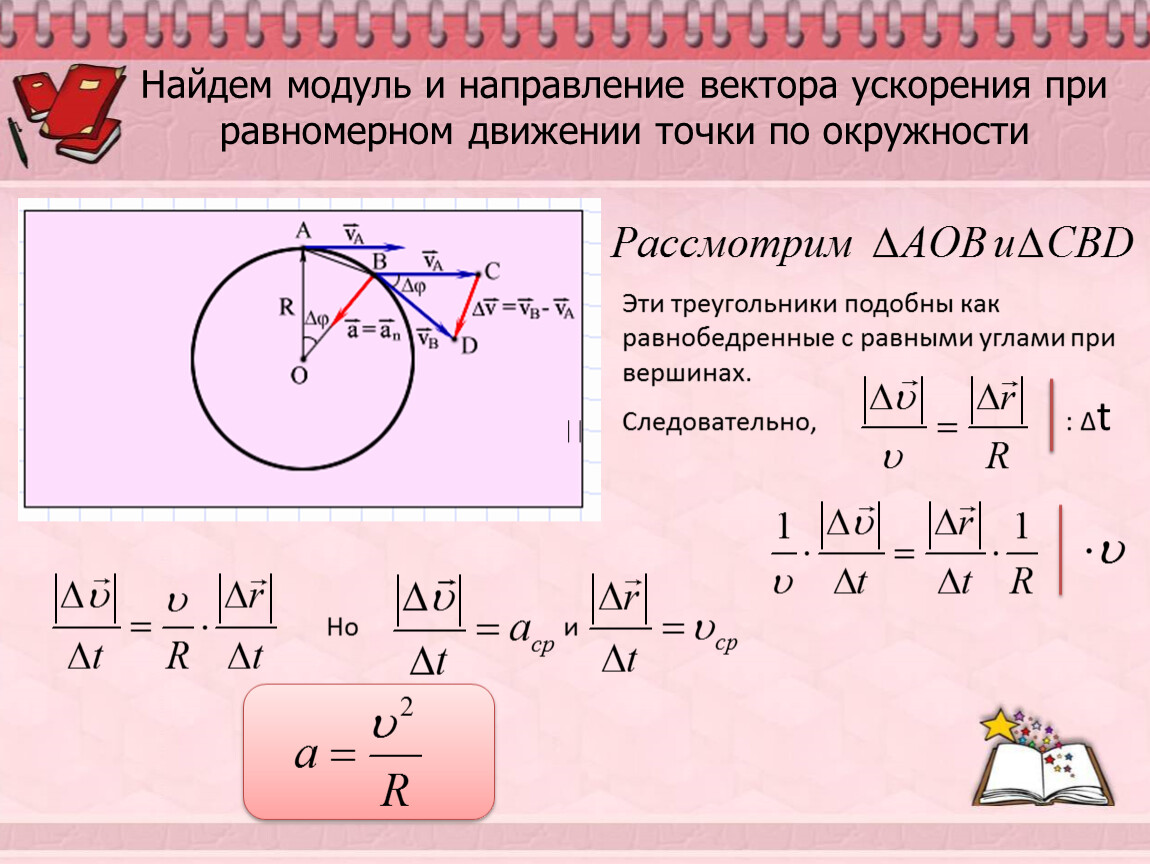
Если объект движется с постоянной угловой скоростью, радиус-вектор будет описывать круг с постоянной величиной скорости.

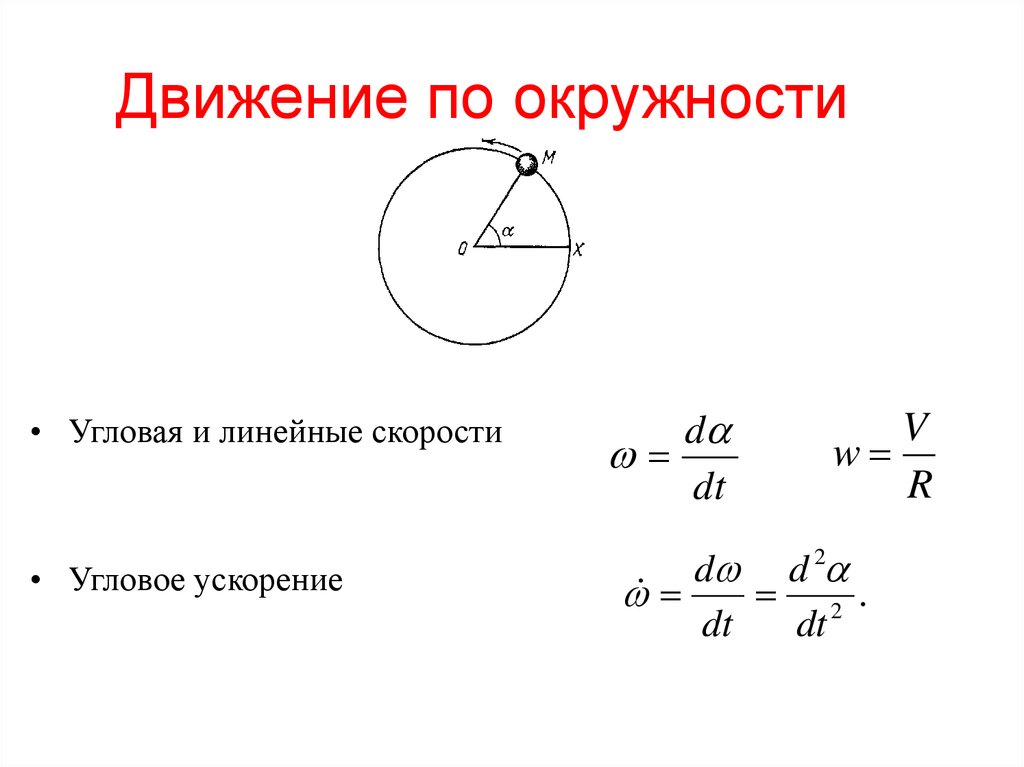
Для изучения изменения радиус-вектора в динамике полезно применять законы Ньютона и второй закон динамики.

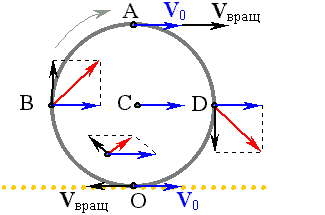
Рассматривая радиус-вектор на окружности, важно учитывать его связь с ускорением, которое зависит от угловой скорости и радиуса.

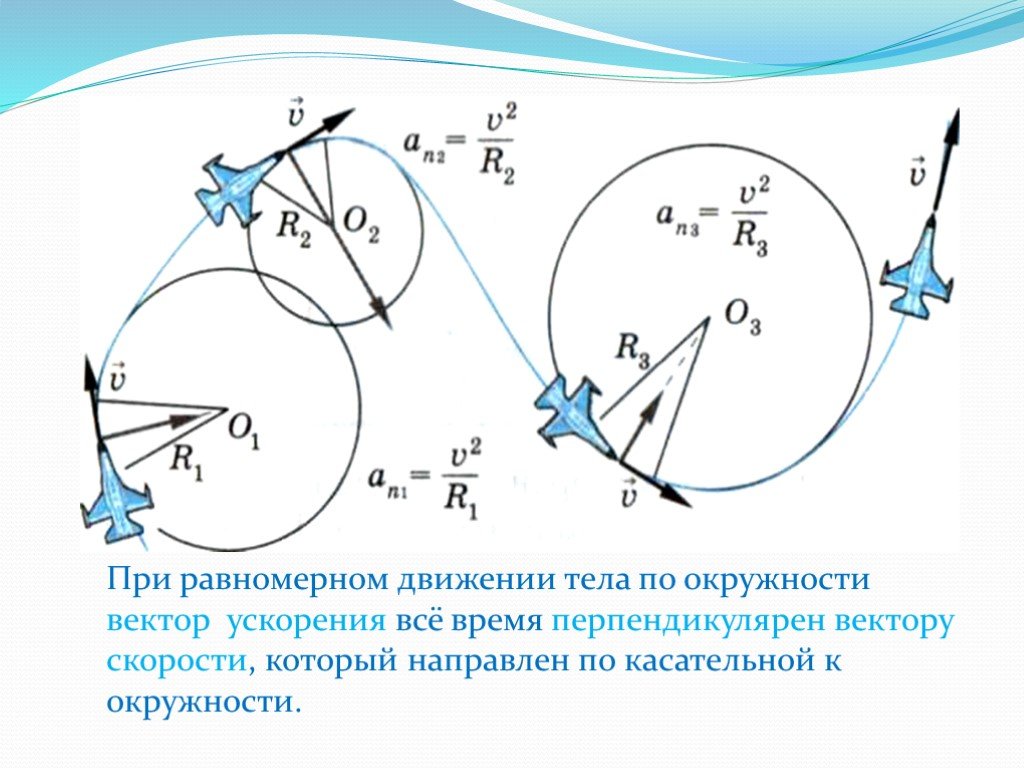
При решении задач на движение по окружности часто используется принцип постоянства угловой скорости для упрощения анализа изменения радиус-вектора.