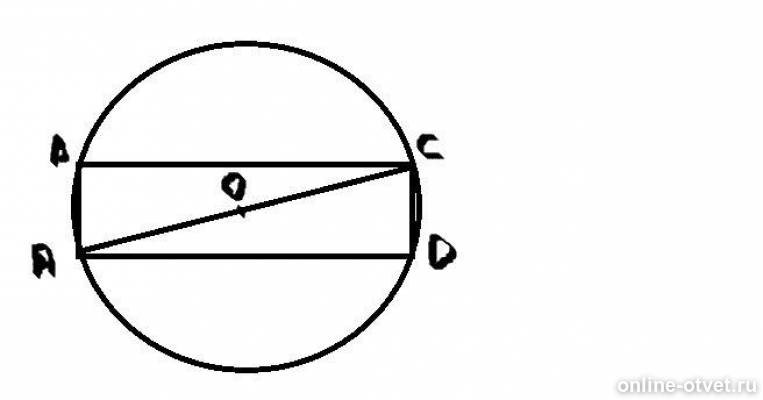
Особенности вычисления площади прямоугольников, вписанных в полуокружность
В данной подборке вы найдете полезные советы и фотографии, которые помогут вам лучше понять концепцию прямоугольника, вписанного в полуокружность, а также способы вычисления его площади и решения подобных задач. Эти знания пригодятся как для школьников, так и для студентов, изучающих геометрию.
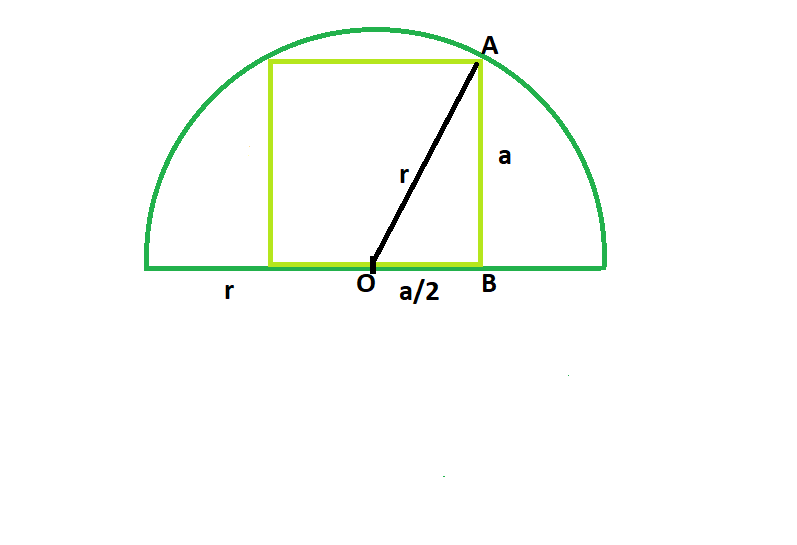

Для решения задачи с прямоугольником, вписанным в полуокружность, важно помнить, что его диагональ является диаметром полуокружности.
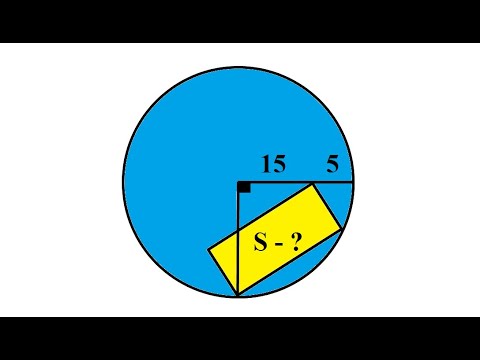
Прямоугольник в окружности


Используйте теорему Пифагора для нахождения сторон прямоугольника, если вам известен его диаметр и одна из сторон.

Тема 8. Прямоугольный треугольник и его описанная и вписанная окружности

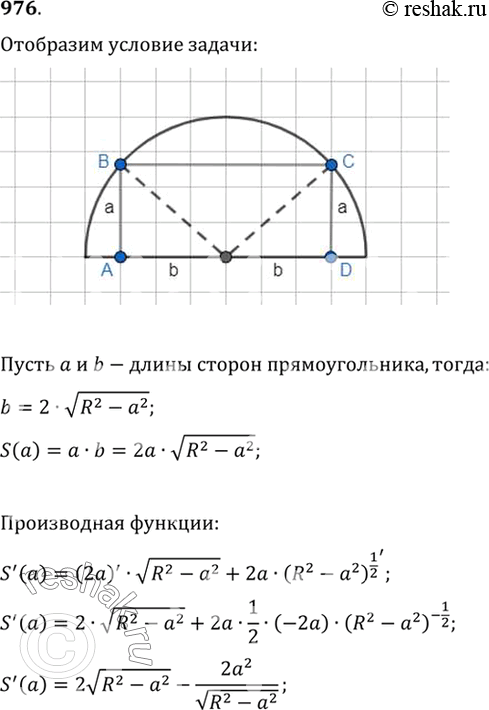
Для расчета площади прямоугольника можно воспользоваться формулой площади: длина умноженная на ширину, где одна из сторон будет вычисляться через радиус полуокружности.

Всё про углы в окружности. Геометрия - Математика

Рассмотрите задачу с конкретными числовыми значениями для лучшего понимания: например, полуокружность с радиусом 5 см. На практике такие задачи часто решаются с помощью подбора.

ОКРУЖНОСТЬ и ПРЯМОУГОЛЬНИК. ГЕНИАЛЬНО!

Не забывайте, что площадь прямоугольника зависит от его пропорций и связи между длиной и шириной, которые можно вычислить через тригонометрические функции углов между сторонами.

Вписанный в окружность прямоугольный треугольник.


Когда вы работаете с прямоугольником, вписанным в полуокружность, всегда проверяйте, что его диагональ точно совпадает с диаметром полуокружности.

Для решения задач с прямоугольниками, вписанными в полуокружность, полезно использовать графическое изображение, чтобы наглядно понять соотношение сторон и углов.

Вписанный угол, опирающийся на диаметр (полуокружность). Геометрия 8-9 класс
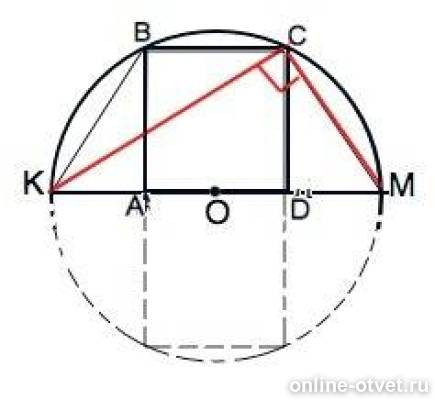
Иногда полезно строить прямоугольник в координатной системе, чтобы легко вычислить его площадь через координаты вершин.

Прямоугольный треугольник вписанный в окружность - Теорема Пифагора

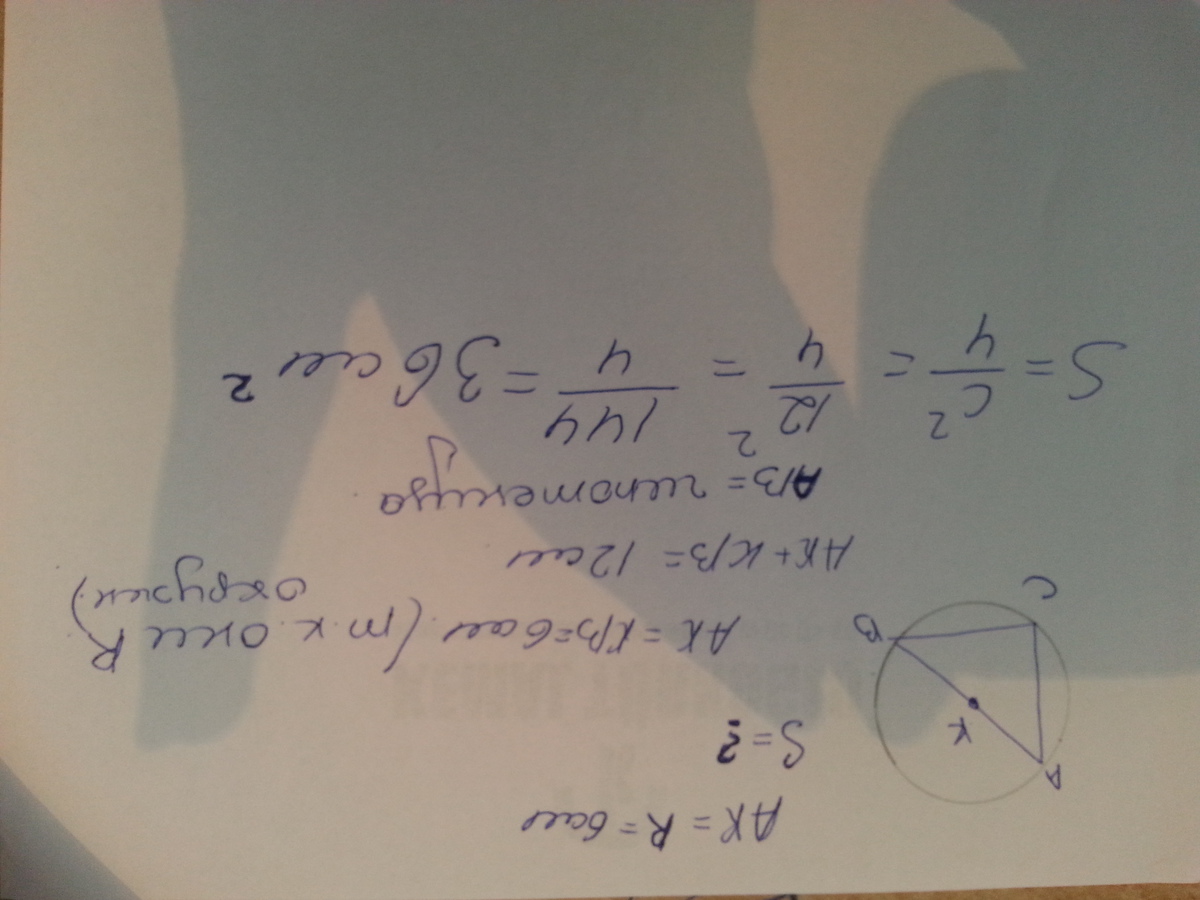
Рассматривая задачу с прямоугольником в полуокружности, всегда обращайте внимание на взаимосвязь радиуса и сторон прямоугольника через углы, так как это существенно упростит расчет.
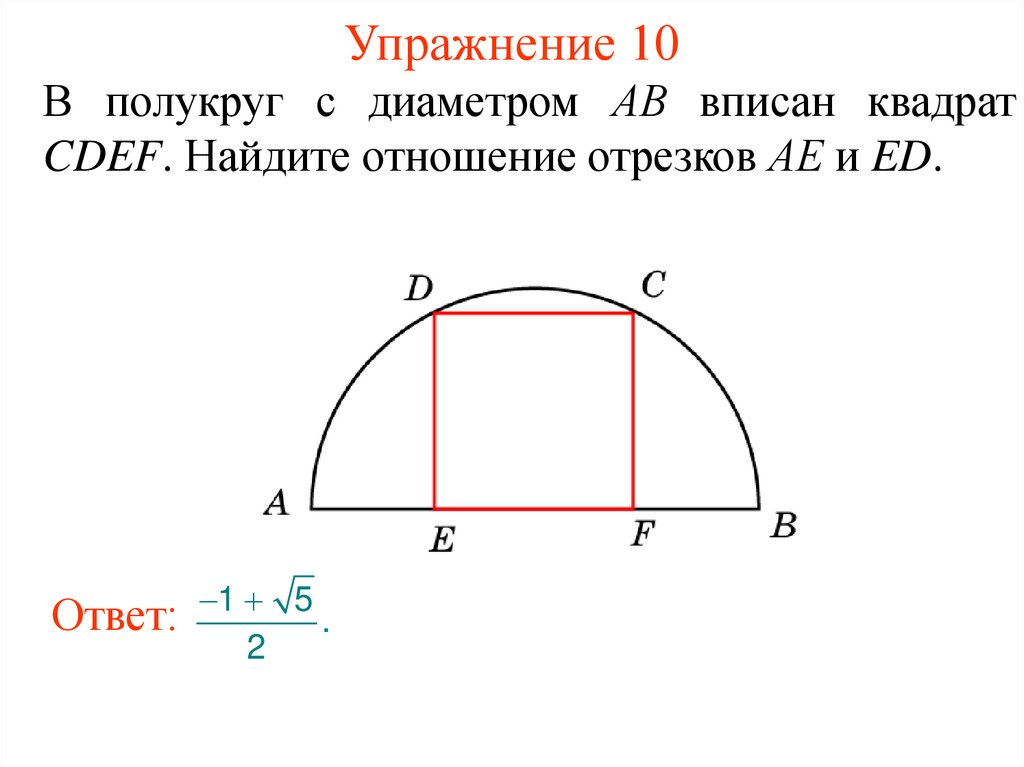

Для более сложных задач используйте дополнительные теоремы о вписанных фигурах, чтобы вывести точные формулы для сторон прямоугольника, если вам известны другие параметры окружности.

Вписанная и описанная окружности - Лайфхак для запоминания