Секущие в окружности: законы и полезные советы
На этой странице вы найдете подборку фотографий, схем и полезных советов, которые помогут понять, как работают пересечения двух секущих в окружности, а также научиться применять геометрические правила в задачах.

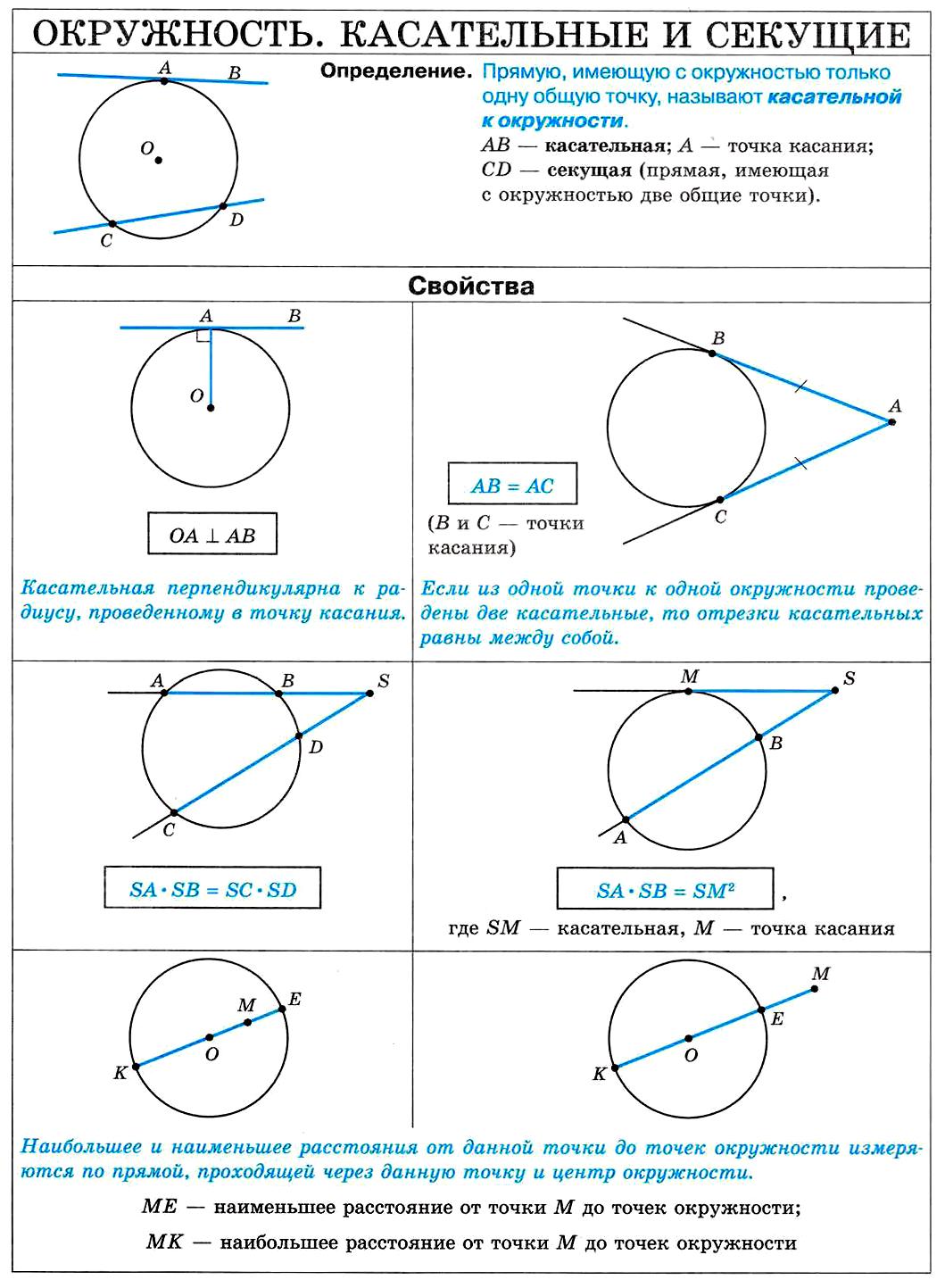
Для решения задач с секущими всегда начертите схематический чертеж, чтобы визуализировать условия.
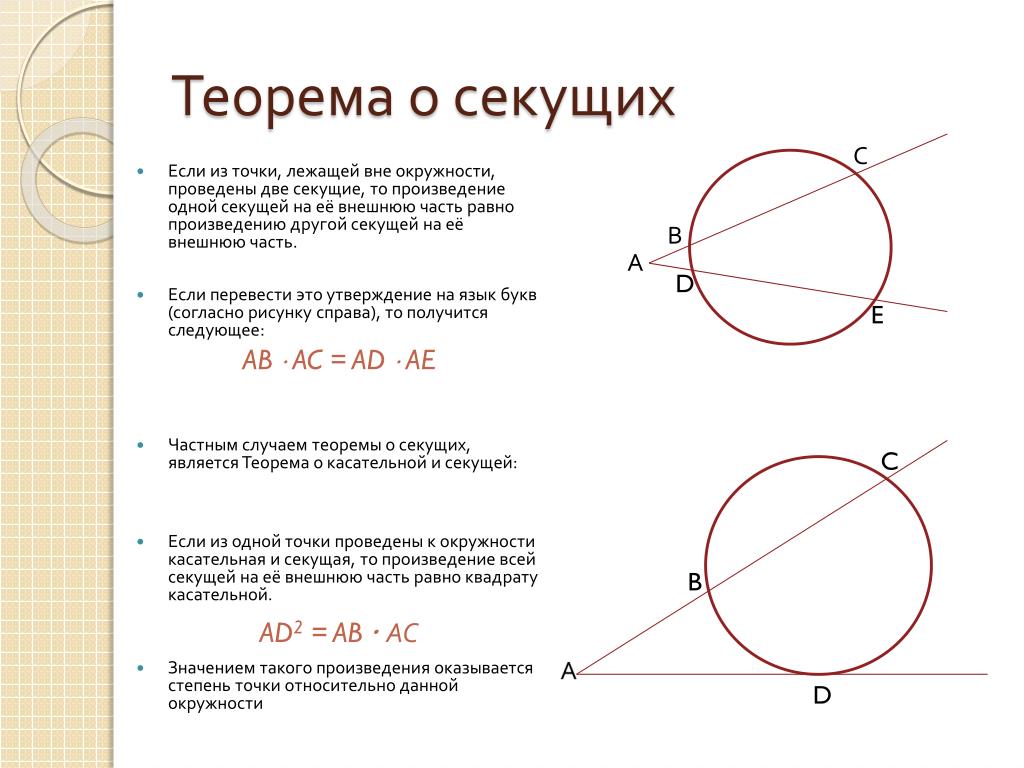
Теорема о двух секущих. 9 класс.

Запомните, что произведение длин отрезков секущей, выходящей из одной точки, всегда одинаково для каждой секущей.

Теорема о секущей и касательной, о секущих, о пересекающихся хордах - Теоремы об окружностях - 1
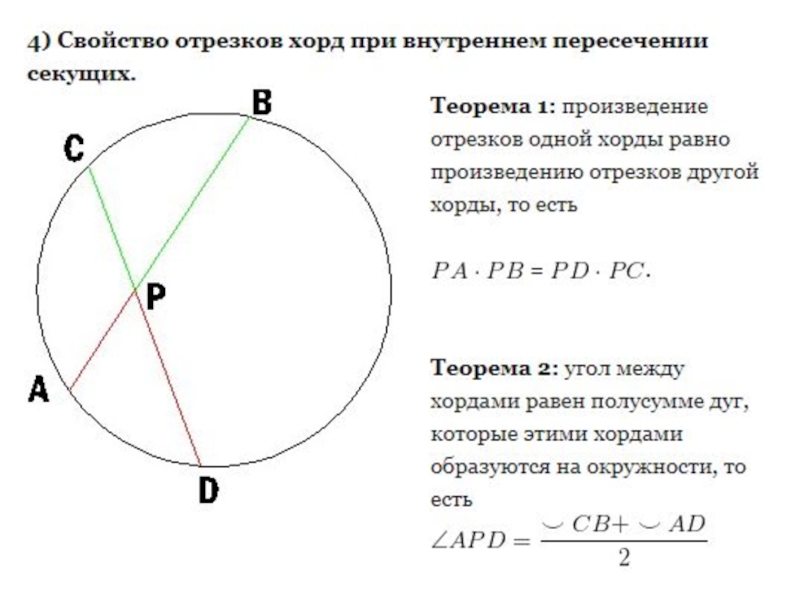
Используйте формулу секущих: PA * PB = PC * PD, где P — точка пересечения секущих, а A, B, C, D — точки их пересечения с окружностью.

Секущие в окружности и их свойство. Геометрия 8-9 класс
При решении задач с окружностями следите за точностью измерений на чертеже, чтобы избежать ошибок в расчетах.

Теорема об отрезках хорд и секущих

Обратите внимание на углы, образованные секущими. Часто они помогают установить дополнительные зависимости.

Всё про углы в окружности. Геометрия - Математика
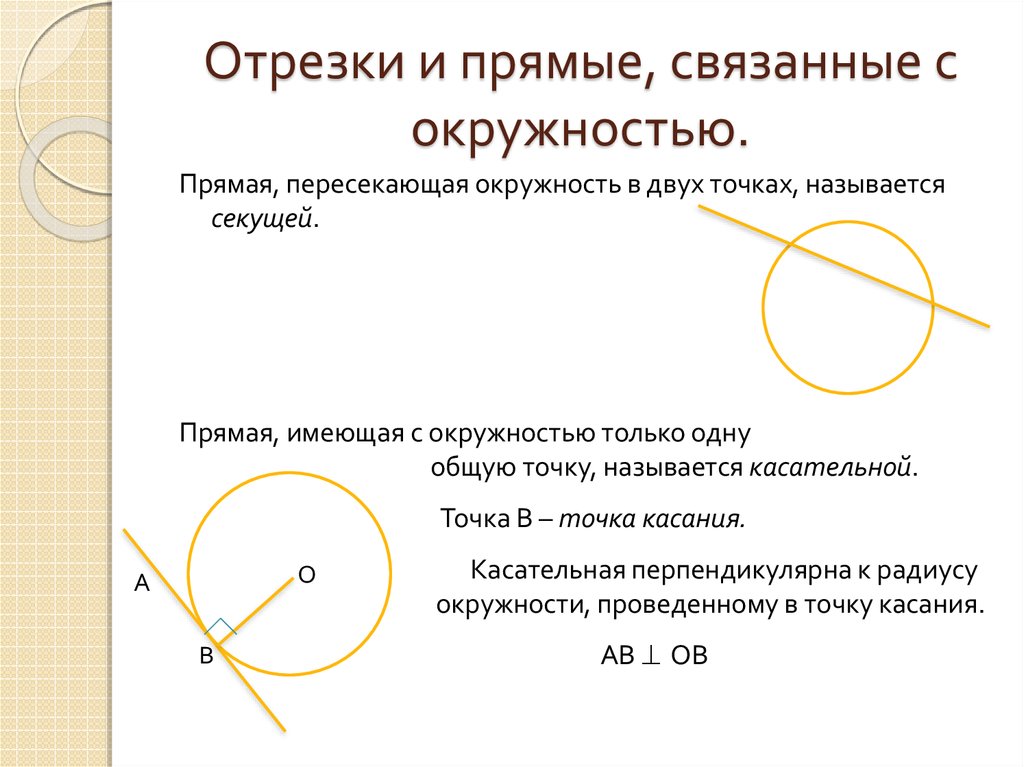
Если задача предполагает нахождение длины отрезков, убедитесь, что все данные правильно соотносятся с условиями.
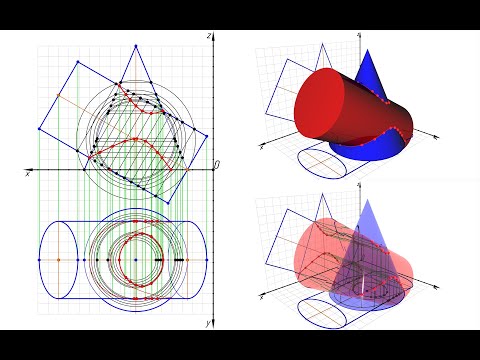
Линия пересечения конуса и цилиндра (метод концентричных секущих сфер)
При необходимости проведите дополнительные линии в окружности, чтобы выделить ключевые треугольники или углы.

Линия пересечения двух поверхностей конус и призма (Метод секущих плоскостей)
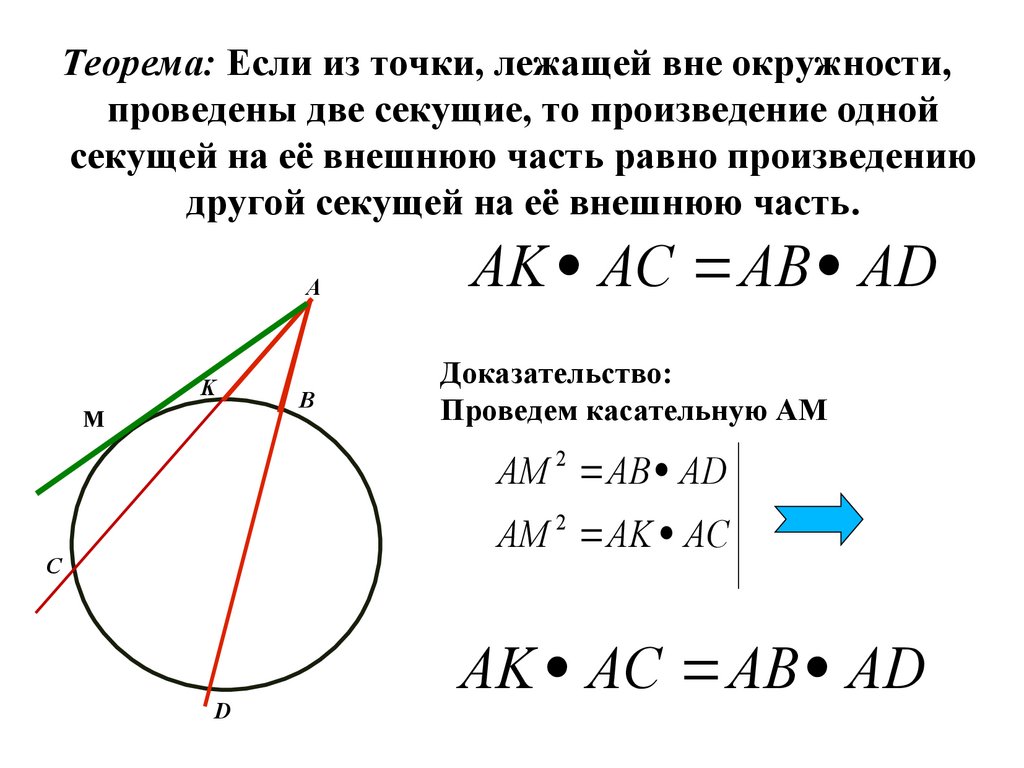
Используйте теорему о мощности точки, чтобы упростить вычисления и проверку результатов.

Начертательная геометрия. Лекция 16. Часть 2.

Окружность, касательная, секущая и хорда - Математика
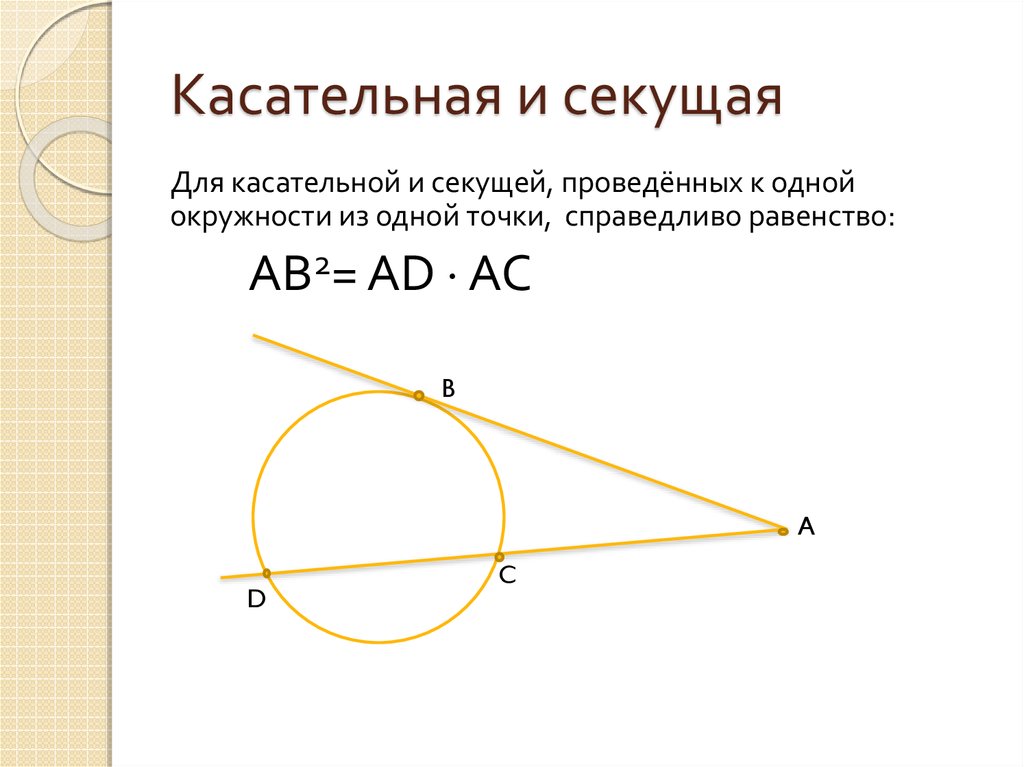
Практикуйтесь с различными задачами, чтобы лучше запомнить закономерности и принципы работы с секущими.

Всегда проверяйте свой ответ, используя обратный расчет или альтернативный способ решения.

Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)
