Все, что нужно знать об отражении точки относительно прямой и ее вычислении
Отражение точки относительно прямой — это важный геометрический процесс, который часто используется в задачах по аналитической геометрии. В этой статье мы рассмотрим формулу для нахождения отражения точки относительно прямой и подробно объясним, как применить этот метод на практике. Вы научитесь находить координаты отраженной точки, а также разберетесь в геометрическом значении данного процесса.

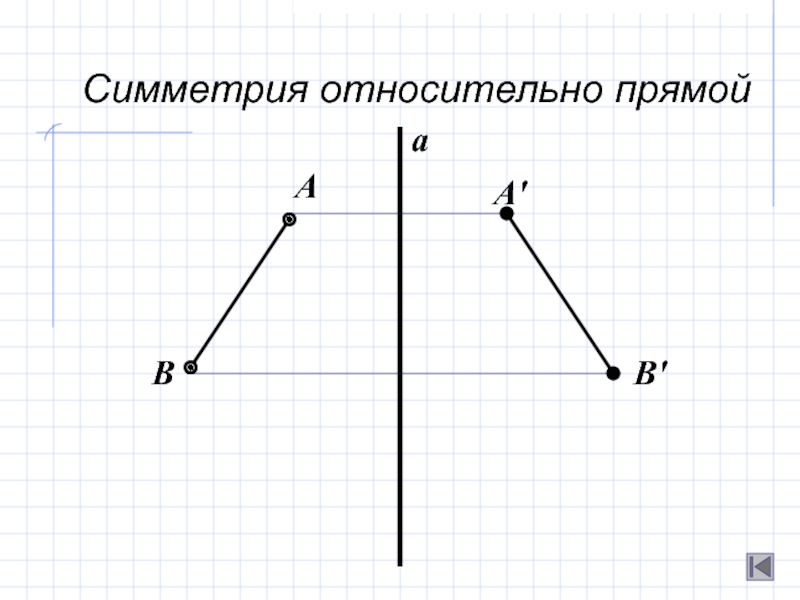
Для нахождения отражения точки относительно прямой важно правильно выбрать координаты прямой, на которую будет происходить отражение. Используйте уравнение прямой в виде ax + by + c = 0.

Как построить точку, симметричную точке А(5;-3) относительно оси Оу Как решить задачу по геометрии

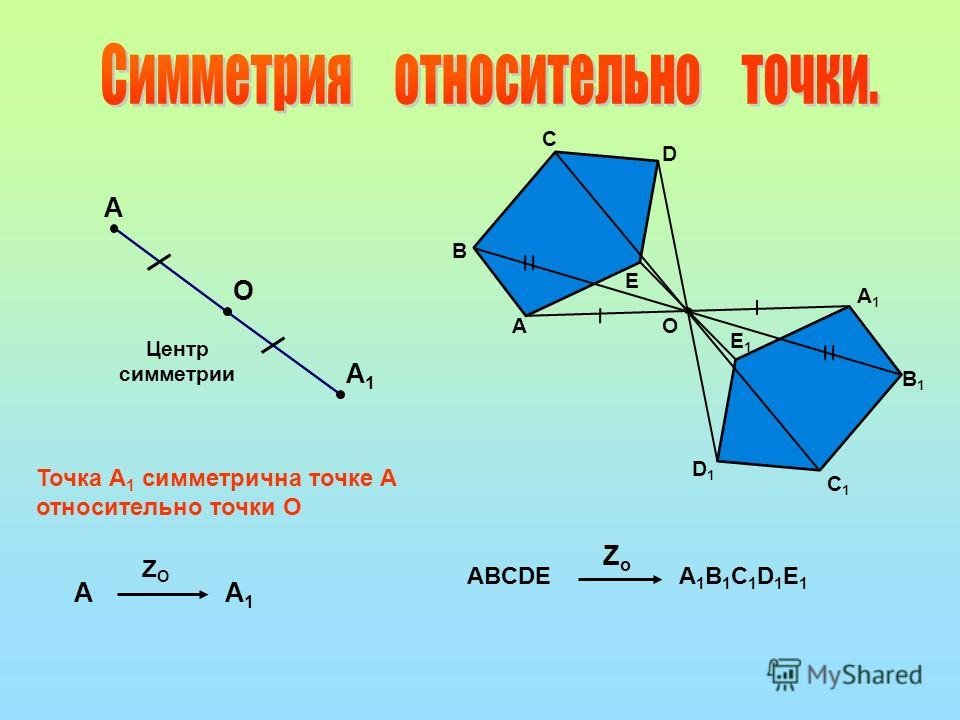
Перед тем как применять формулу для отражения, убедитесь, что точка и прямая заданы в одинаковых координатах (например, все в декартовой системе). Это облегчит вычисления.

§ 4. Симметрия относительно точки. Математика 6 класс. Герасимов

Для вычисления отраженной точки используйте формулы, основанные на расстоянии от точки до прямой и ее проекции на прямую. Это позволяет точнее определить место нахождения зеркального отражения.

Симметрия относительно точки (центральная симметрия). Пример 2
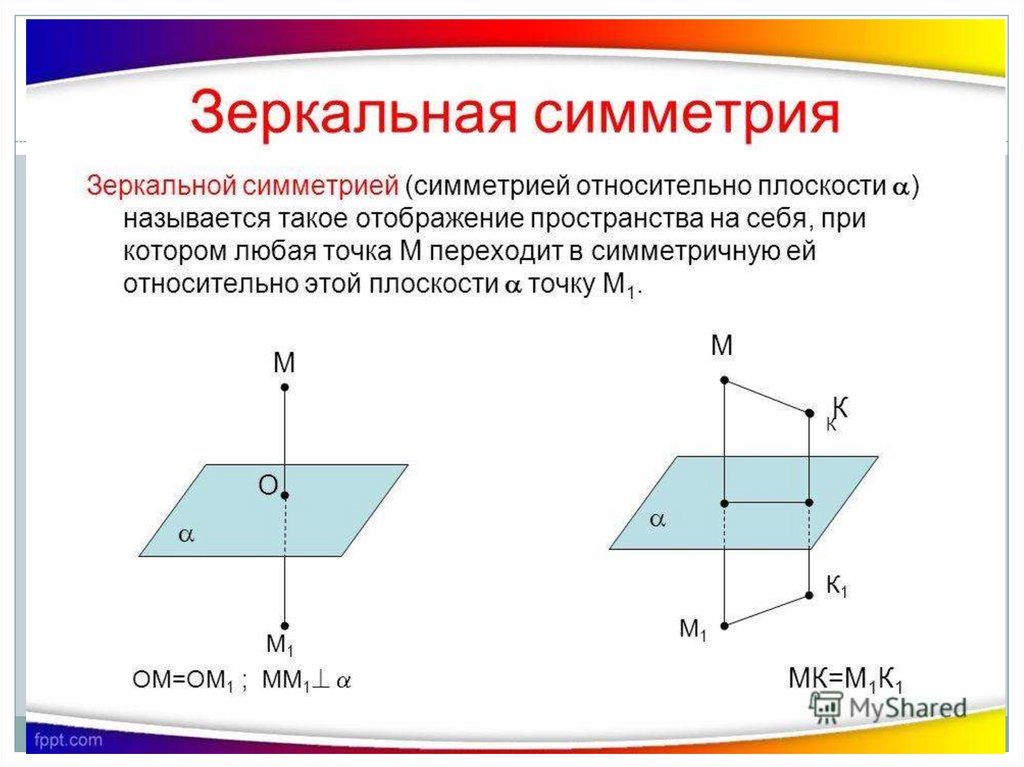
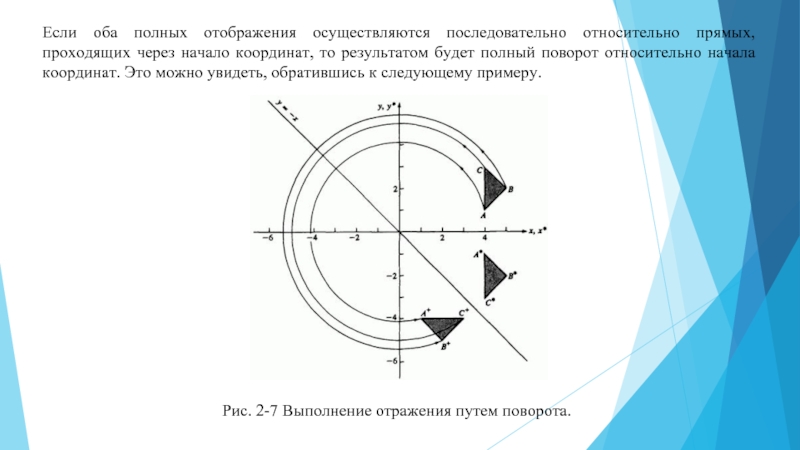
Когда рассчитываете отражение точки относительно прямой, не забывайте о возможных особенностях прямых, например, их наклоне. Чем более наклонная прямая, тем более сложными могут быть вычисления.
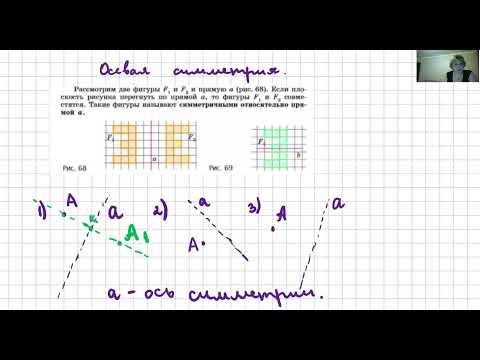
Осевая симметрия.
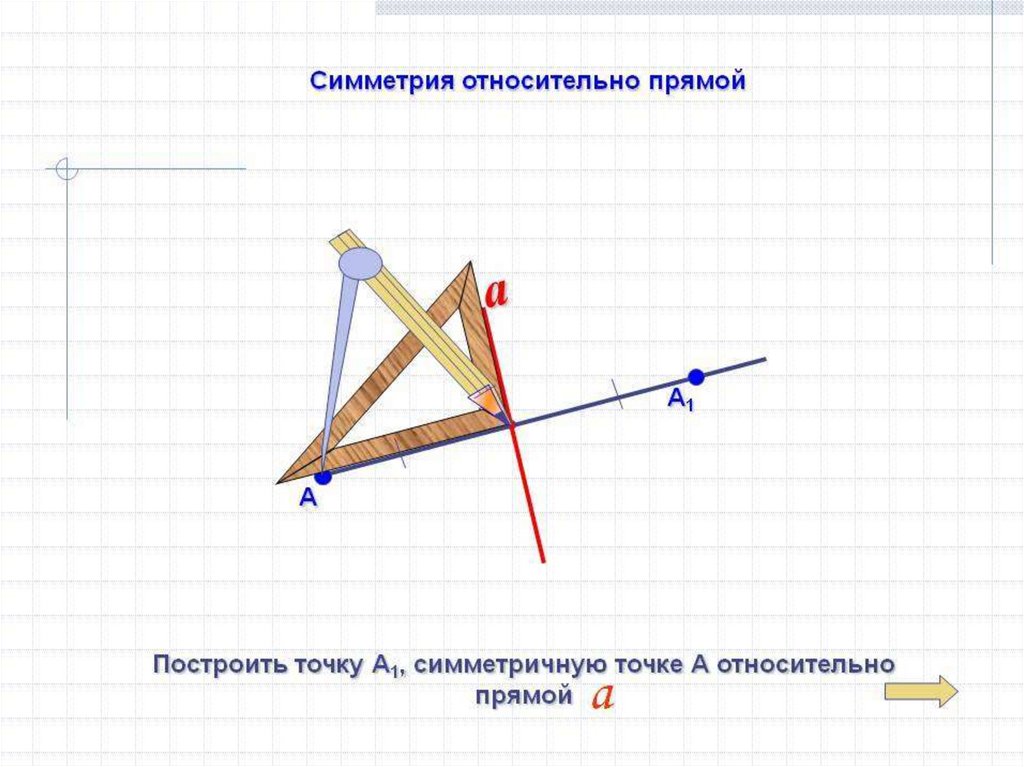
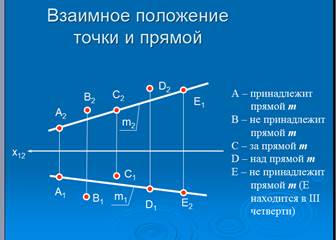
Для упрощения вычислений можно использовать геометрические методы, такие как нахождение перпендикуляра от точки до прямой. Это часто позволяет избежать сложных алгебраических манипуляций.

Построение симметричной точки относительно плоскости Н или V
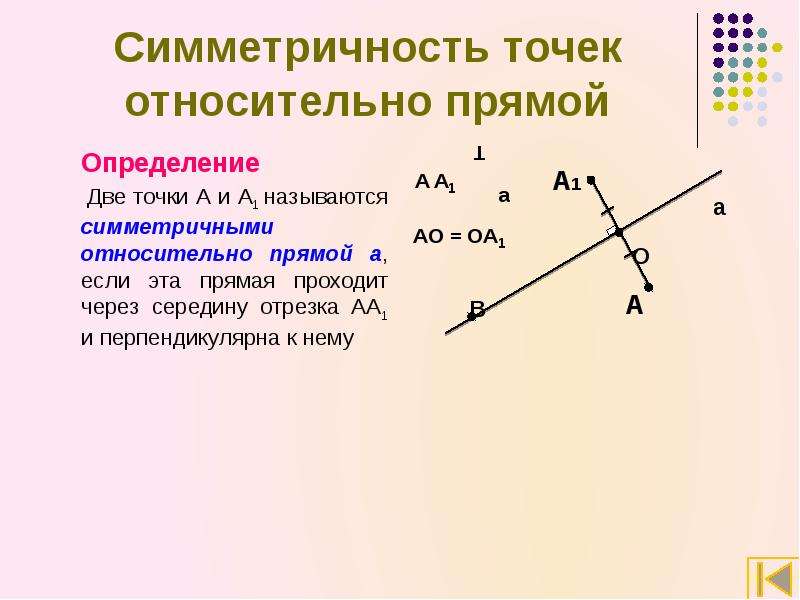
Если прямая вертикальная или горизонтальная, вычисление отражения значительно упрощается, так как в этих случаях отражение происходит вдоль одной из осей.

Короткие загадки, которые осилит не каждый профессор

При решении задач на отражение точки полезно использовать симметричные свойства геометрии, такие как зеркальность относительно осей координат.
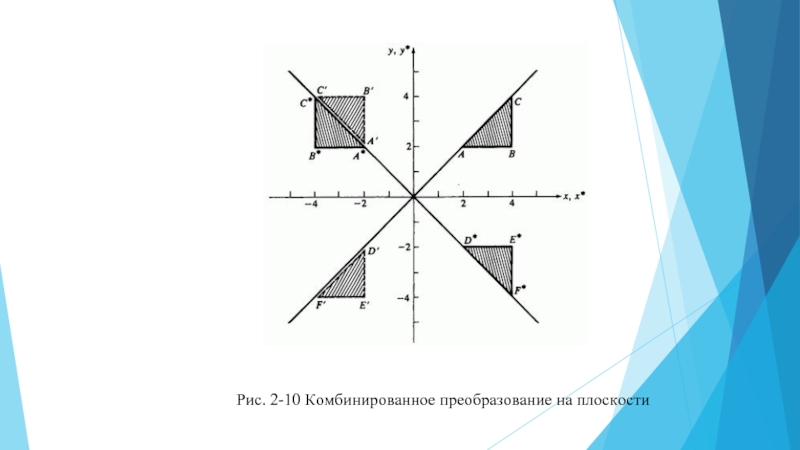
Если вам нужно отразить точку относительно прямой, которая проходит через начало координат, важно учесть, что отраженная точка будет иметь симметричные координаты по отношению к оси этой прямой.

Построение фигур, симметричных относительно заданной точки или прямой. Часть 1

Симметрия относительно прямой (осевая симметрия). Пример 2
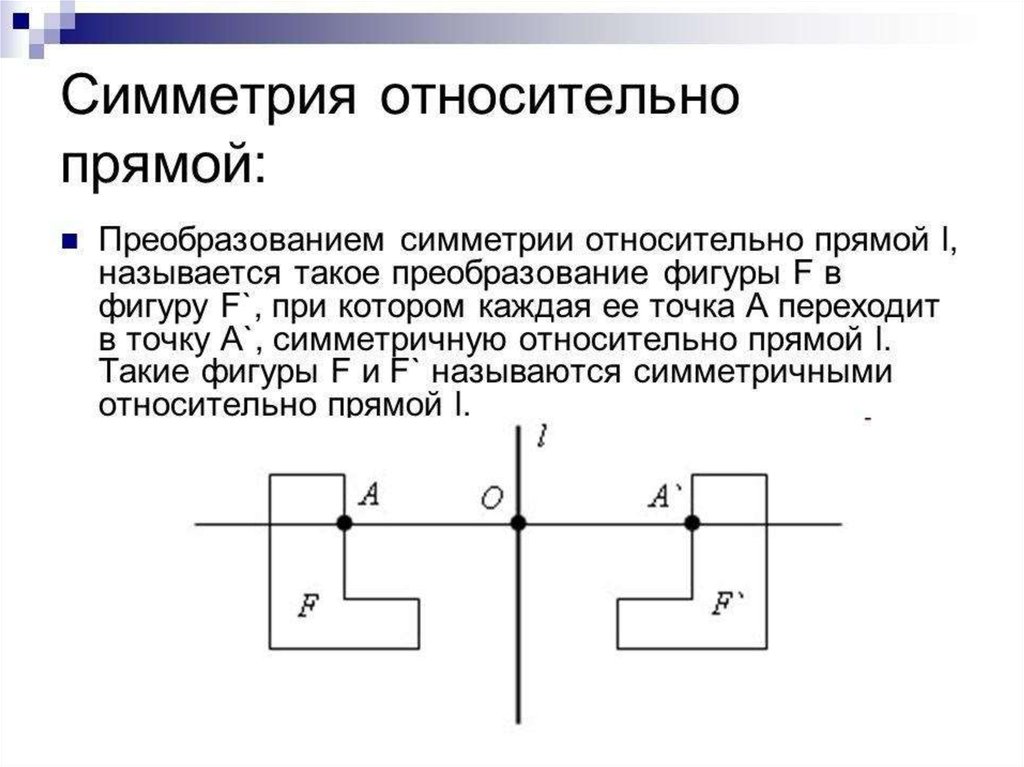
Практика в решении задач поможет вам лучше понять, как работает формула отражения и в каких случаях она может быть адаптирована для разных типов прямых.

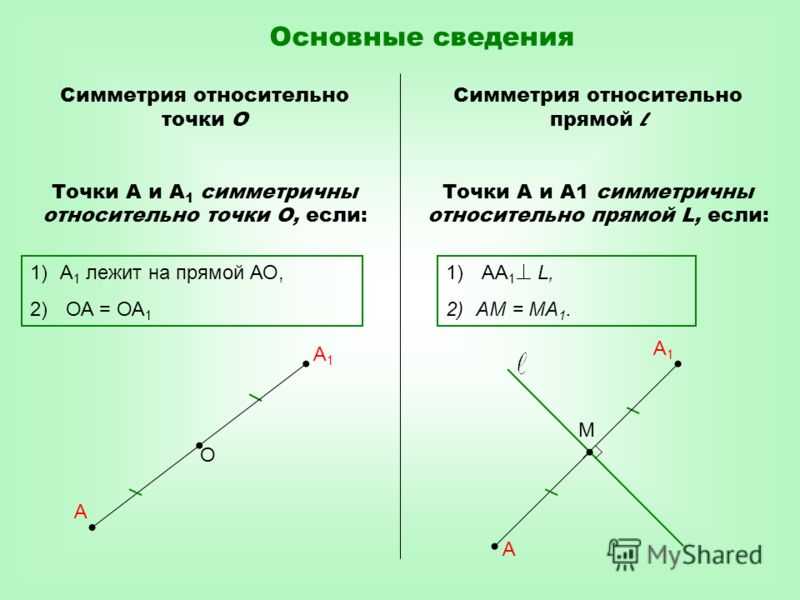
Для более сложных задач полезно использовать графическое представление, чтобы наглядно увидеть процесс отражения и убедиться в правильности вычислений.


Как ПОБЕДИТЬ в перечневой олимпиаде? - Мой опыт, советы и подготовка со Школково