Как правильно найти определитель матрицы: ключевые шаги и полезные рекомендации

Определение матрицы является важным элементом линейной алгебры. В этой статье мы подробно объясним, что такое определитель матрицы, как его вычислить и в каких случаях его используют. Также вы найдете пошаговые инструкции, примеры и советы, которые помогут вам легко справиться с задачами, связанными с матрицами.

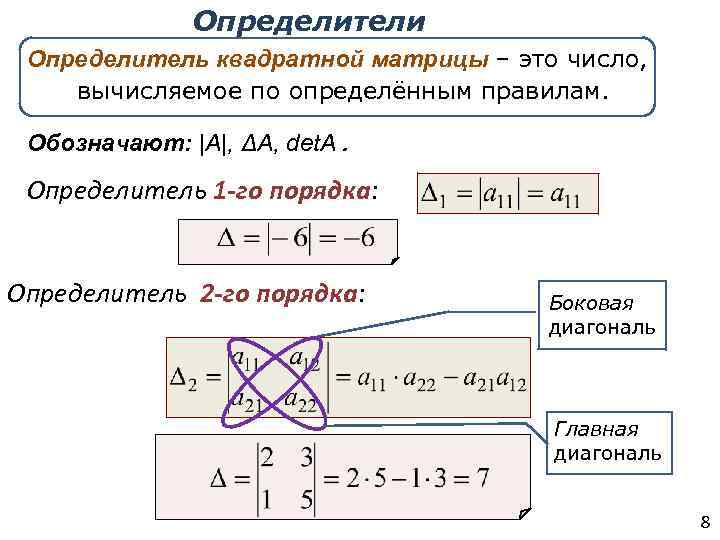
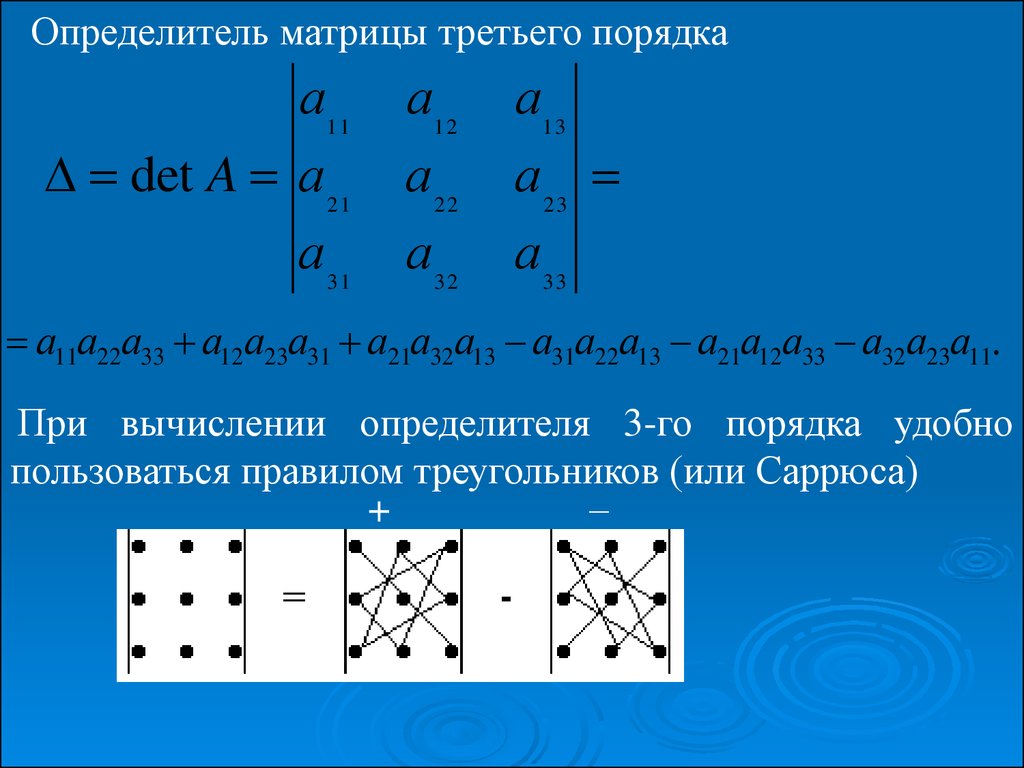
Для вычисления определителя матрицы 3x3 используйте формулу: определитель = a(ei - fh) - b(di - fg) + c(dh - eg), где элементы матрицы записаны как a, b, c, d, e, f, g, h, i.

Для матриц размером 4x4 и выше используйте метод разложения по строкам или столбцам. Это поможет уменьшить размер задачи и упростить вычисления.

Когда работаете с большими матрицами, иногда полезно применять методы упрощения, такие как приведение матрицы к верхнетреугольному виду.

Помните, что если матрица имеет нулевой ряд или столбец, ее определитель равен нулю.

Если матрица симметрична, определитель можно вычислить быстрее, используя дополнительные свойства симметричных матриц.

Для проверки правильности вычислений определителя всегда можно воспользоваться калькулятором или специализированным программным обеспечением, чтобы сравнить результаты.

Если матрица имеет ранг 1, то ее определитель всегда равен нулю, это может существенно ускорить решение задачи.

При решении системы линейных уравнений через матрицы важно помнить, что если определитель коэффициентной матрицы равен нулю, система либо несовместна, либо имеет бесконечно много решений.

Не забывайте, что если строки или столбцы матрицы линейно зависимы, ее определитель тоже равен нулю.

Для поиска определителя больших матриц воспользуйтесь разложением по минорным матрицам, это значительно упростит расчет.