Основы работы с множествами комплексных чисел
Комплексные числа играют важную роль в математике и инженерии. Знание операций над ними, таких как сложение, вычитание, умножение и деление, поможет эффективно решать задачи и понимать их применение в различных областях.


Перед началом изучения операций на множестве комплексных чисел убедитесь, что вы понимаете их алгебраическую форму: a + bi, где a — действительная часть, b — мнимая, а i — мнимая единица.
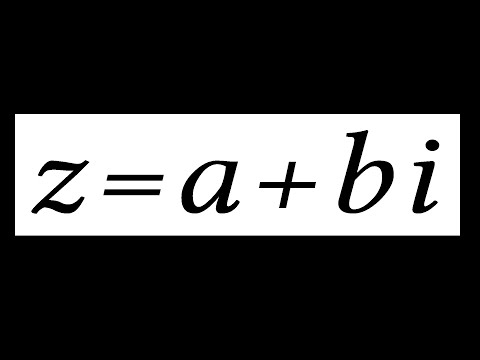
КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТ

Для сложения комплексных чисел сложите их действительные и мнимые части по отдельности: (a1 + b1i) + (a2 + b2i) = (a1 + a2) + (b1 + b2)i.

Алгебра и геометрия 30. Группы (продолжение). Поле комплексных чисел

При вычитании комплексных чисел вычитайте их действительные и мнимые части по отдельности: (a1 + b1i) − (a2 + b2i) = (a1 − a2) + (b1 − b2)i.

Математика без Ху%!ни. Комплексные числа, часть 1. Введение.

Умножение комплексных чисел можно представить как распределительное действие: (a1 + b1i)(a2 + b2i) = a1a2 + a1b2i + b1a2i + b1b2i², учитывая, что i² = −1.

Канунников А.Л. - Математика для школьников - 19. Поле комплексных чисел

Для деления комплексных чисел используйте формулу: (a + bi) ÷ (c + di) = [(ac + bd) + (bc − ad)i] / (c² + d²).
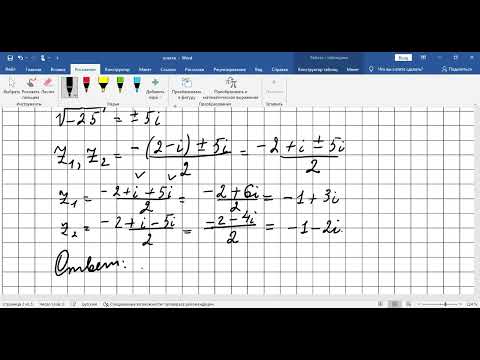
Решение КВУР на множестве комплексных чисел


Модуль комплексного числа |z| равен квадратному корню из суммы квадратов его действительной и мнимой частей: |a + bi| = √(a² + b²).

Преобразование в тригонометрическую форму облегчает работу с умножением и делением: z = r(cos φ + i sin φ), где r — модуль, а φ — аргумент числа.

Билет 12 (Комплексные числа, операции, формы записи)
При сложении или вычитании в тригонометрической форме преобразуйте числа обратно в алгебраическую форму для удобства вычислений.

Используйте свойства сопряженных чисел: умножение числа на его сопряженное дает действительное число, равное квадрату модуля.

Комплексные числа: коротко и понятно – Алексей Савватеев - Лекции по математике - Научпоп

Регулярно решайте задачи, связанные с комплексными числами, чтобы укрепить свои знания и навыки работы с ними.
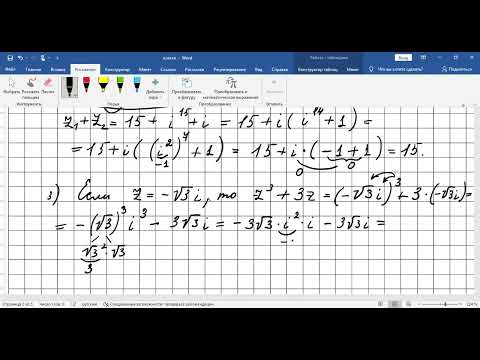
Арифметические операции на множестве комплексных чисел сложение, вычитание, умножение, деление
