Исследование влияния вписанной окружности на свойства треугольников и их применение
Окружность, вписанная в треугольник, является важным элементом в геометрии, оказывающим влияние на множество свойств фигуры, таких как площади, углы и соотношения сторон. На этой странице мы подробно рассмотрим, как она влияет на треугольники, и предложим практические советы по использованию этой концепции в решении задач.
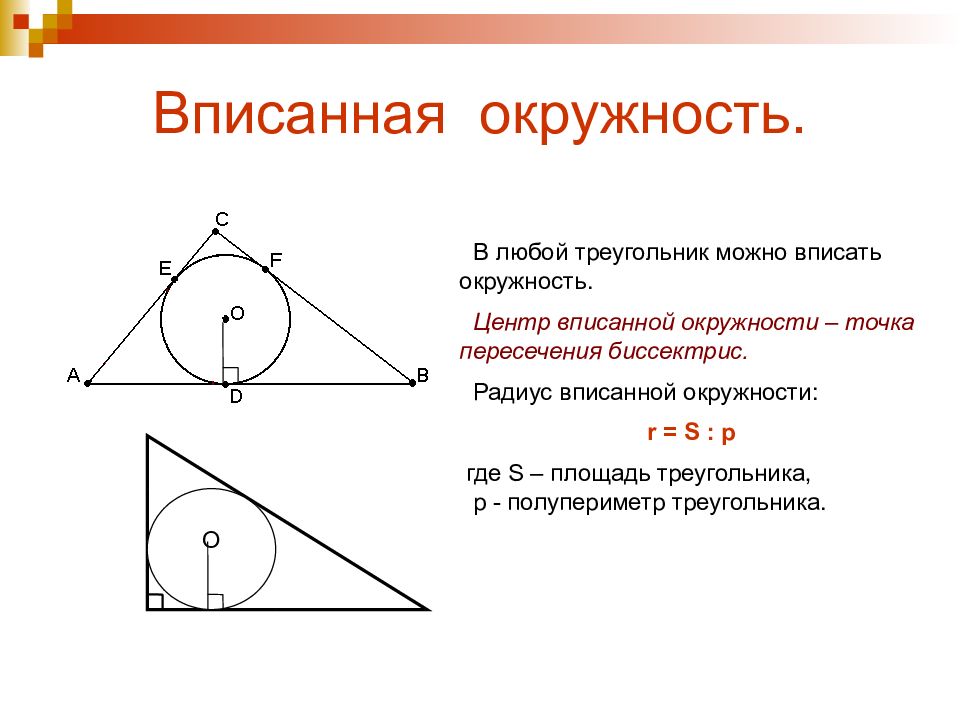
Обратите внимание, что радиус вписанной окружности зависит от площади треугольника и его полупериметра, что важно для быстрого вычисления его размеров.

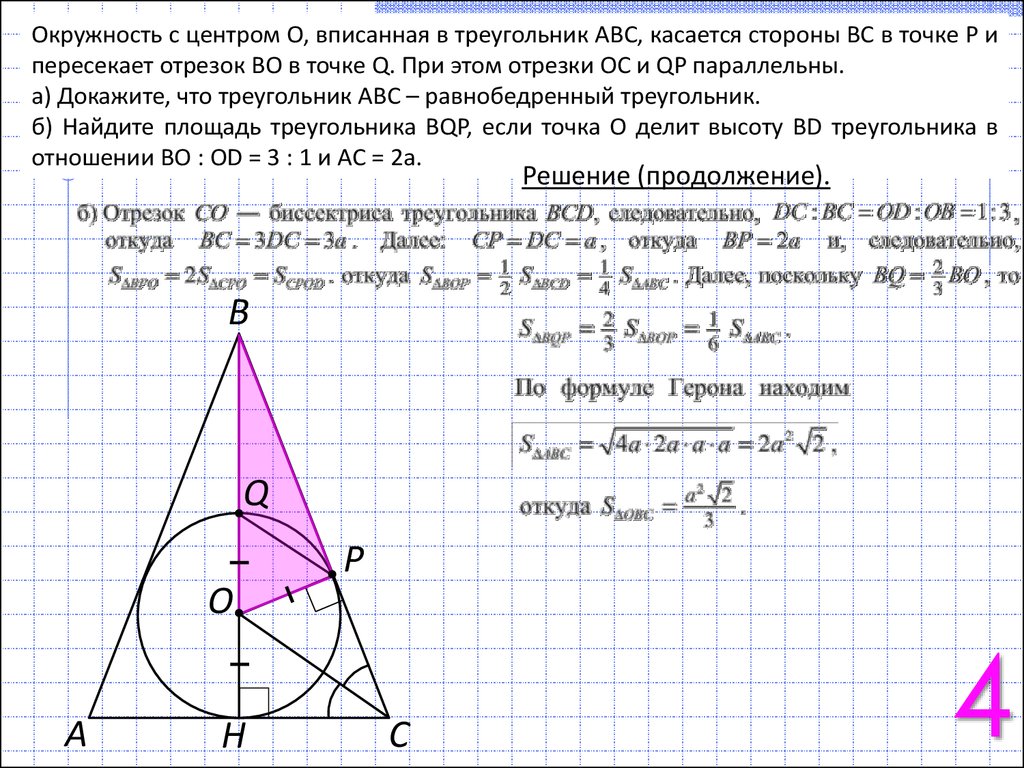
Строим вписанную в данный треугольник окружность (Задача 2).

Для нахождения радиуса вписанной окружности используйте формулу: r = S / p, где S — площадь треугольника, а p — его полупериметр.
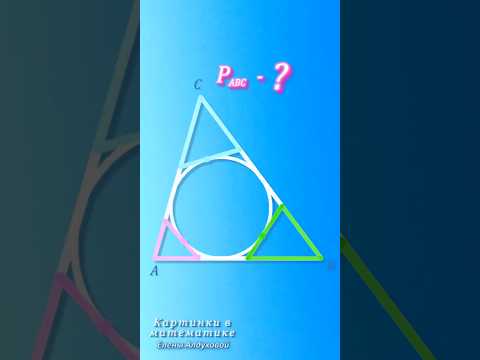
К окружности, вписанной в ∆ ABC, проведены три касательные. Найти периметр ✧ #КартинкиВМатематике

При решении задач, связанных с вписанной окружностью, важно помнить о её касаниях с каждой стороной треугольника, так как это помогает определить длины отрезков, образующих касательные.

Вписанная и описанная окружности - Лайфхак для запоминания


В задачах с треугольниками и окружностями всегда старайтесь визуализировать фигуры, чтобы лучше понять их взаимное расположение и применить нужные теоремы.

ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэ

Если нужно найти центр вписанной окружности, помните, что он расположен в точке пересечения биссектрис углов треугольника.
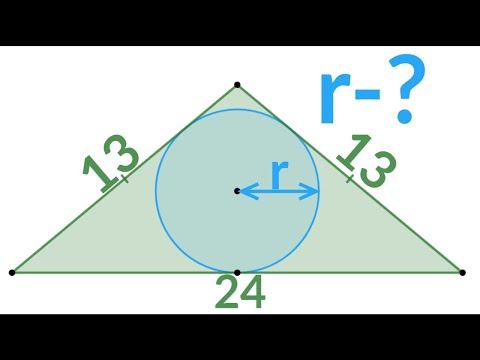
Сможешь найти радиус вписанной окружности?
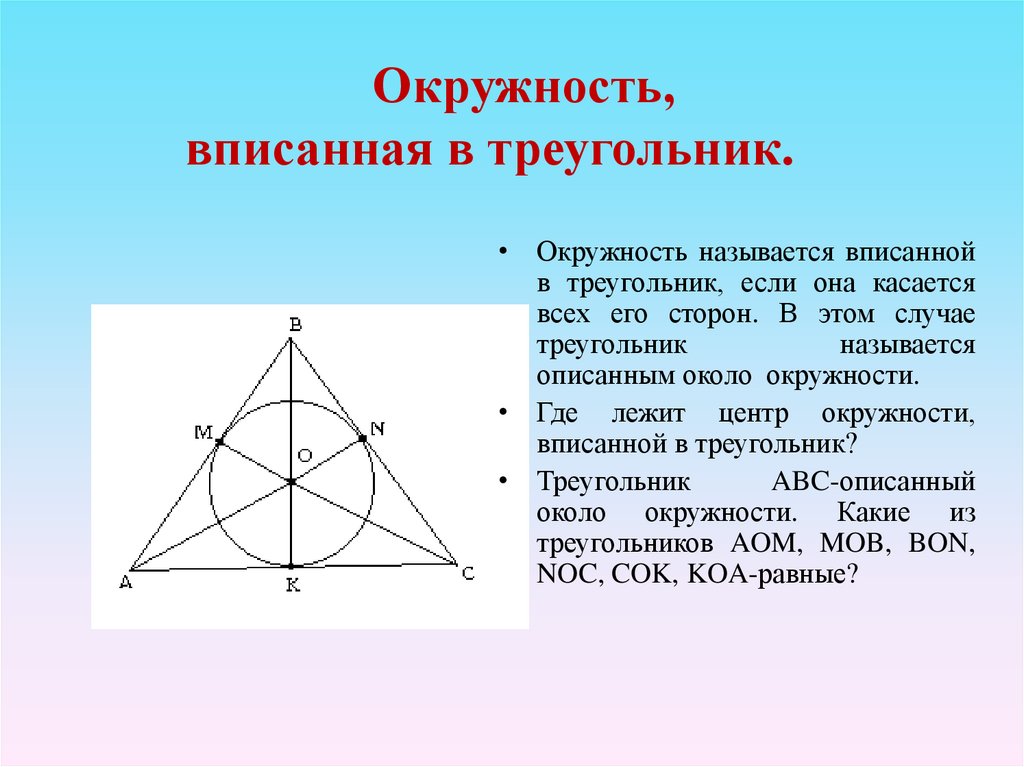
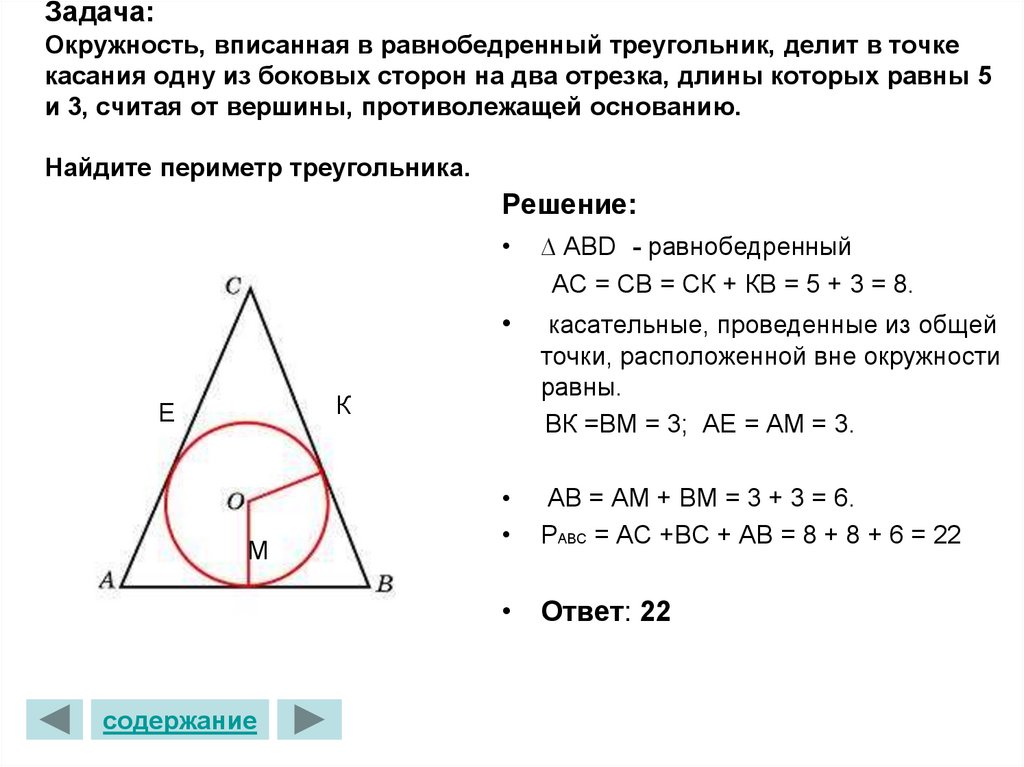
Для треугольников с известными сторонами, можно использовать формулу Герона для вычисления площади, что поможет в дальнейшем расчёте радиуса вписанной окружности.
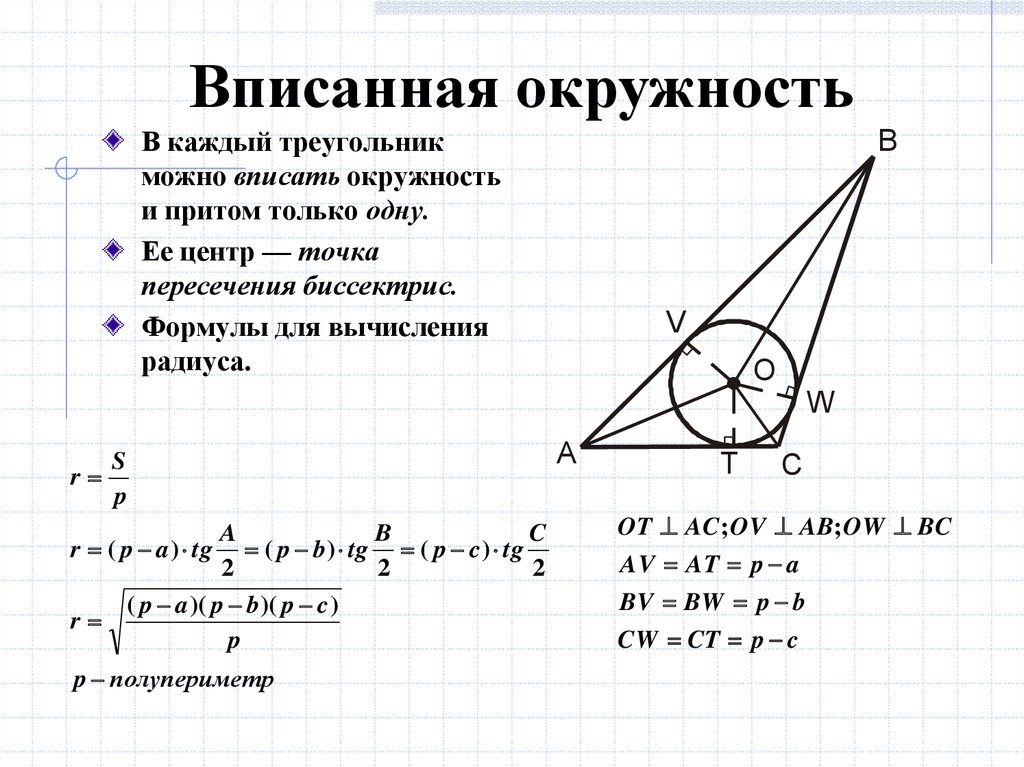
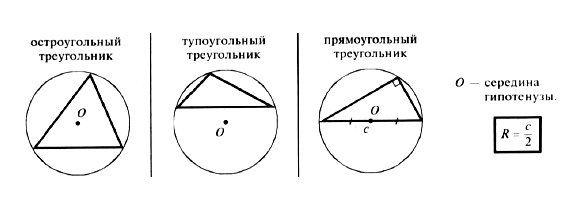
Если треугольник прямоугольный, то радиус вписанной окружности можно вычислить как r = (a + b - c) / 2, где a и b — катеты, а c — гипотенуза.

Окружность вписана в треугольник так,что образует у вершины ромб

Использование вписанной окружности в задачах на доказательства может значительно упростить нахождение соотношений между сторонами треугольника.

Всё про углы в окружности. Геометрия - Математика
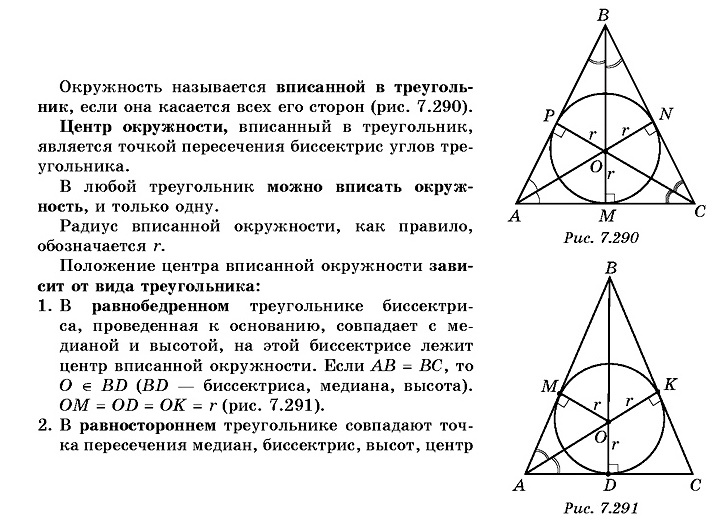
Помните, что для любого треугольника, если известны длины сторон и площадь, то можно найти радиус вписанной окружности, что полезно при решении более сложных геометрических задач.
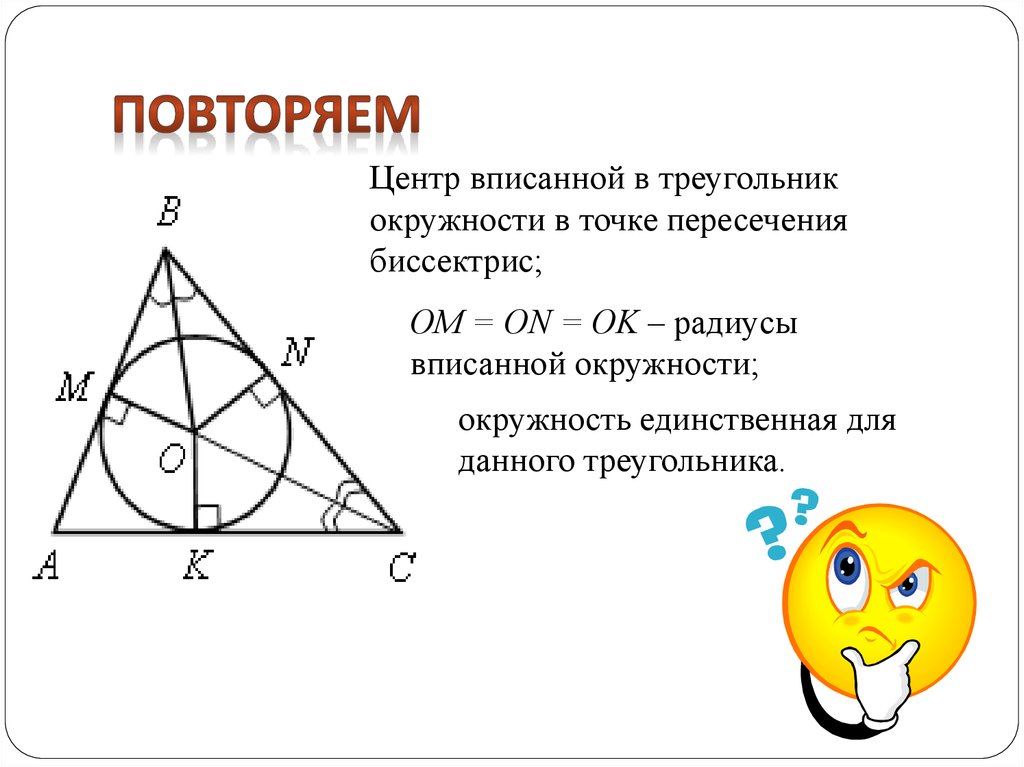
Изучение свойств вписанных окружностей помогает глубже понять взаимосвязь между различными геометрическими объектами, такими как треугольники, окружности и их центры симметрии.
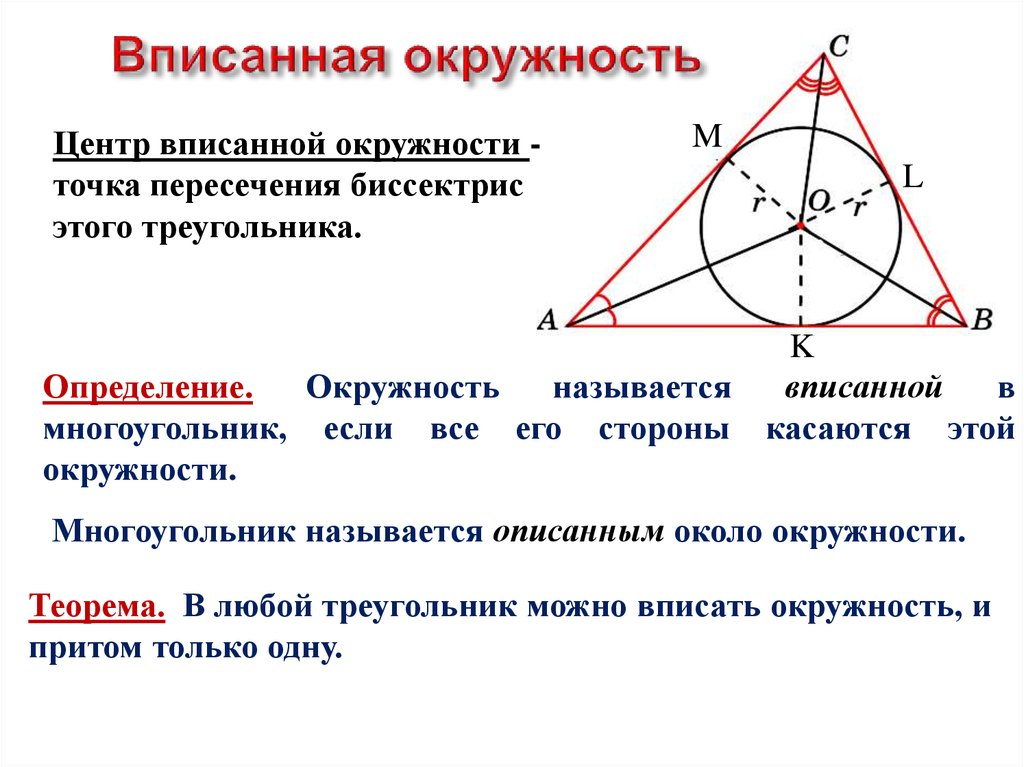

Математика за минуту: Формула радиуса вневписанной окружности в произвольный треугольник.