Методы расчета объемов тел вращения в полярной системе координат
На этой странице вы найдете подборку фотографий и подробные советы о том, как правильно и эффективно вычислять объем тел вращения, используя полярные координаты. Погрузитесь в тонкости математических расчетов и визуализации для более глубокого понимания этой темы.
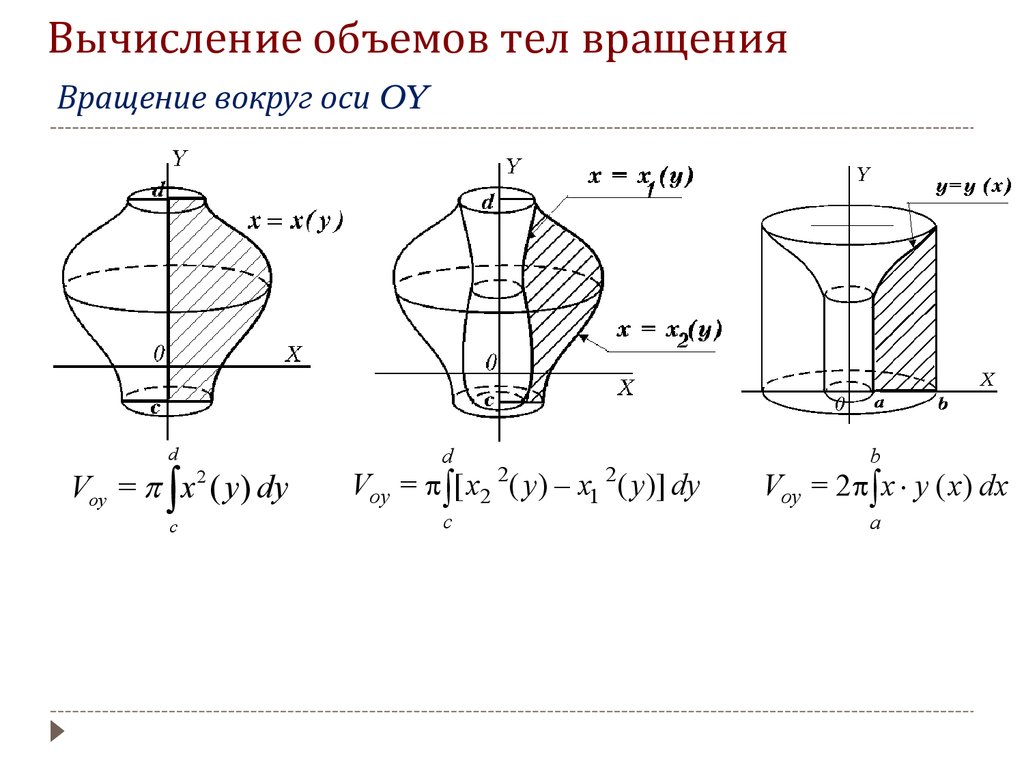

Изучите формулу для расчета объема через интеграл в полярных координатах: V=π∫ab[R(θ)]2dθV = /pi /int_{a}^{b} [R(/theta)]^2 d/thetaV=π∫ab[R(θ)]2dθ.

Тела вращения (задание 5). Что нужно знать для ЕГЭ? - Математика ЕГЭ 2022 - Умскул


Перед началом расчетов убедитесь, что у вас правильно определены пределы интегрирования [a,b][a, b][a,b].

Определенный интеграл. Методы интегрирования. Объём тела вращения. Олимпиадные задания

Нарисуйте схему тела вращения, чтобы визуализировать его форму и упростить постановку задачи.

Вычисление площадей фигур и объемов тел в полярных координатах. (Интегралы - урок 22)

Используйте симметрию тела вращения для упрощения вычислений, если это возможно.

Лекция 5. Приложения определенных интегралов. Площадь фигуры. Длина кривой. Объем тела вращения
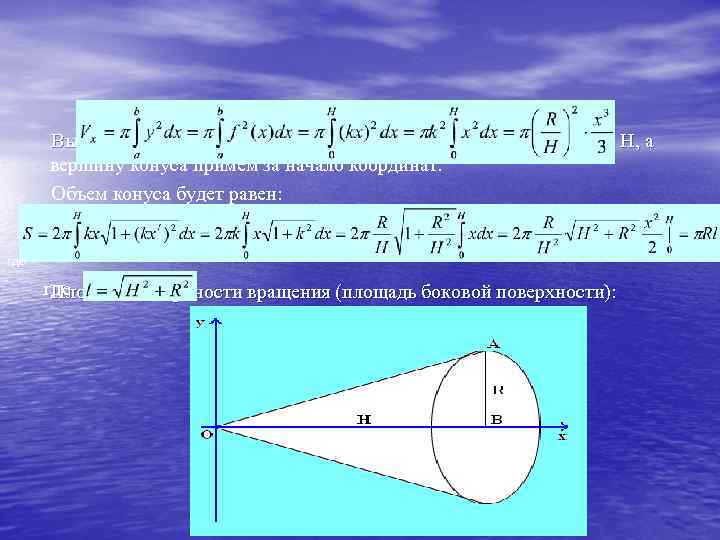
Проверьте правильность выражения радиуса R(θ)R(/theta)R(θ), который задает форму тела в полярных координатах.

Интегралы №13 Объем тела вращения


Убедитесь, что используете корректные единицы измерения для углов: градусы или радианы.

Если интеграл сложно вычислить аналитически, примените численные методы, такие как метод трапеций.
Используйте специализированные программы или калькуляторы для проверки результатов интегрирования.

Объем тела вращения на примере тора. 2 способа
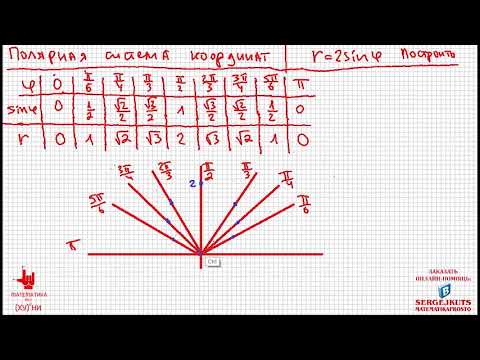
Математика Без Ху%!ни. Полярные координаты. Построение графика функции.
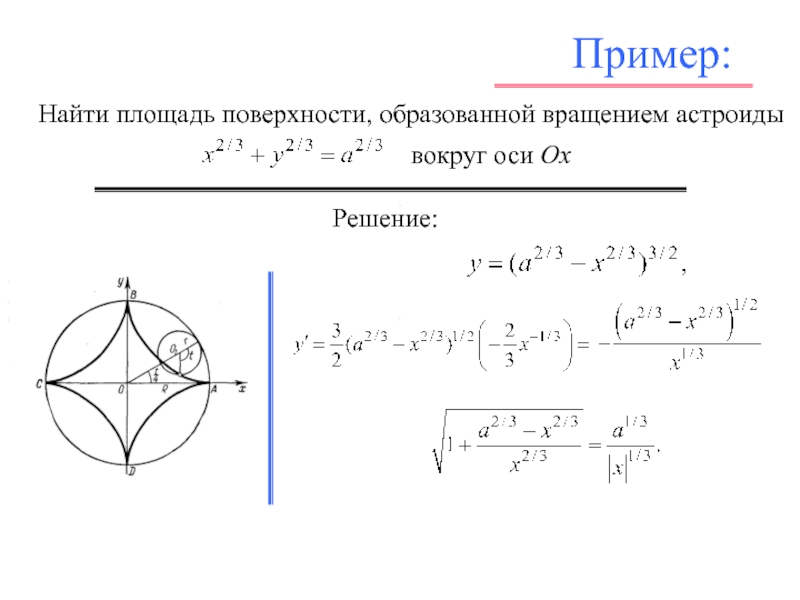
Для более глубокого понимания изучите примеры с шагами решения аналогичных задач.

Видеоурок \


После расчета объема проверьте его физическую интерпретацию, чтобы убедиться в реалистичности результата.
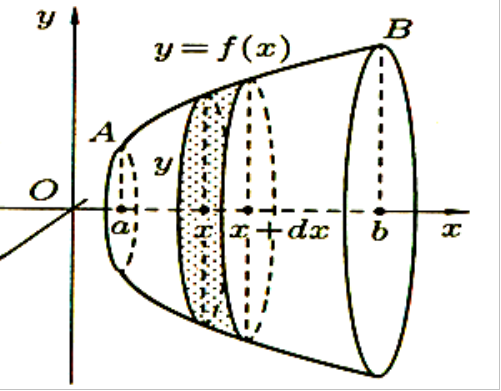
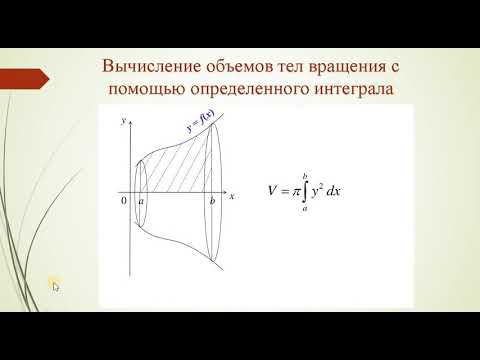
Вычисление объемов тел вращения (применение определенного интеграла)