Простые шаги для определения точек на круге радиусом 1
Узнайте, как находить координаты точек на единичной окружности, используя простые формулы и геометрические приемы. Практические советы и примеры помогут вам быстро освоить методику.


Запомните, что единичная окружность имеет радиус, равный 1, а центр совпадает с началом координат (0, 0).

10 класс, 11 урок, Числовая окружность


Для нахождения координат используйте формулы: x = cos(θ), y = sin(θ), где θ — угол в радианах.

Как видеть тангенс? Тангенс угла с помощью единичного круга.
Работайте с углами в радианах для удобства расчетов, особенно если используете тригонометрические функции.

ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по Математике

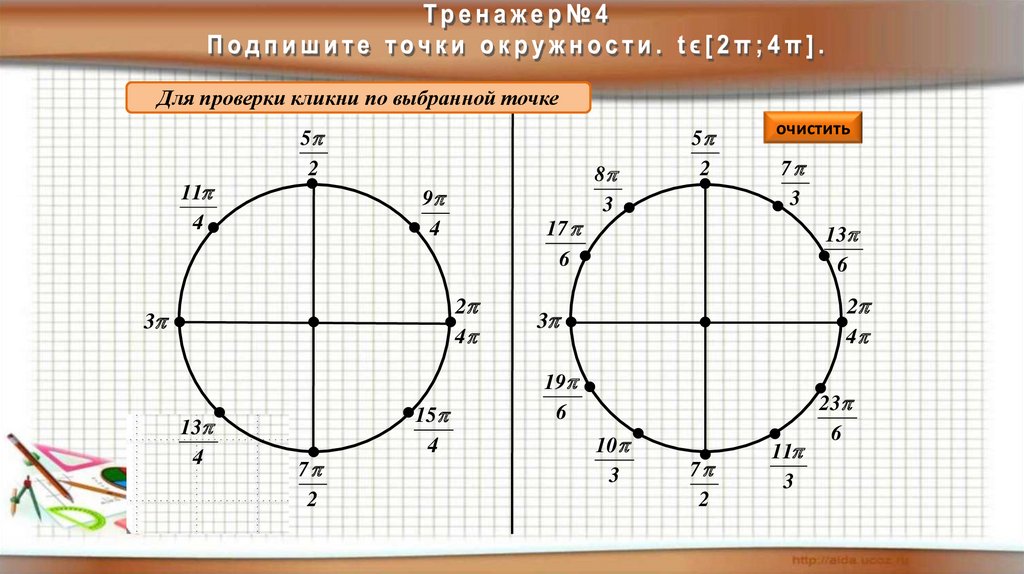
Проверьте результат: сумма квадратов координат любой точки должна равняться 1 (x² + y² = 1).

Как искать точки на тригонометрической окружности.
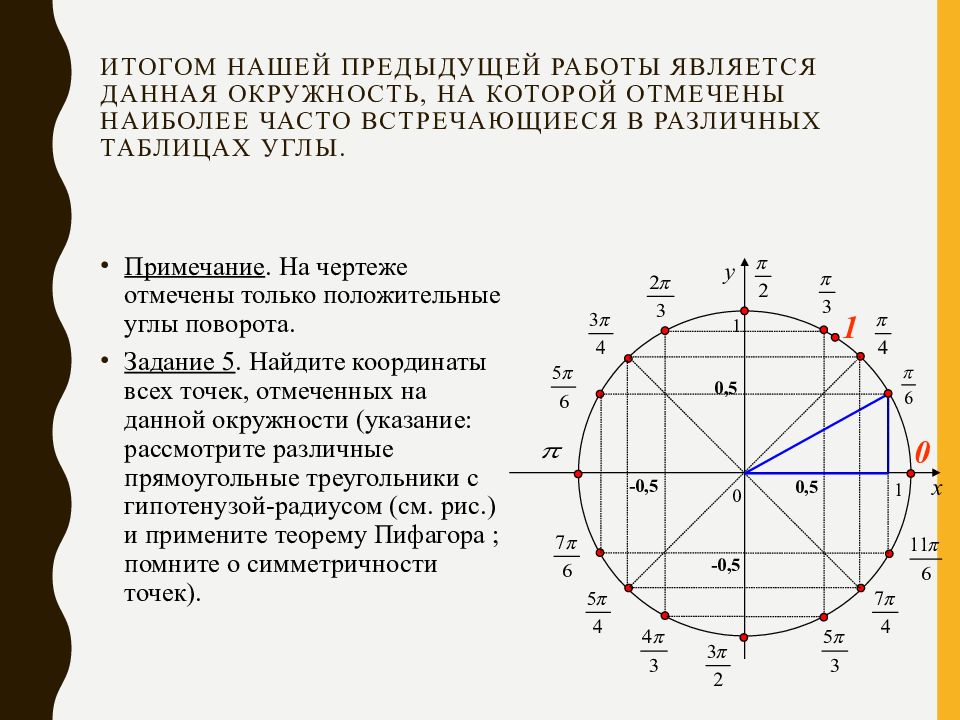
Воспользуйтесь таблицами тригонометрических функций для наиболее популярных углов, таких как 0, π/2, π, 3π/2.

Как найти координаты точек на тригонометрической окружности
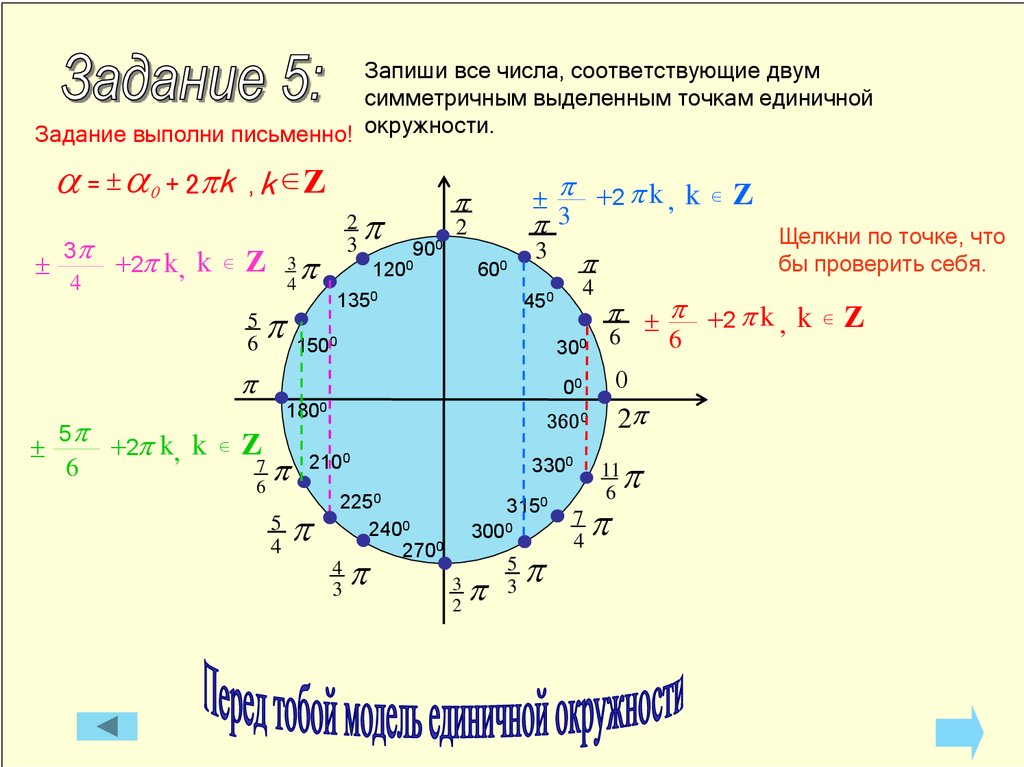

Для визуализации используйте графический редактор или онлайн-калькуляторы, чтобы рисовать окружности и отмечать точки.
Тригонометрическая окружность. Как выучить?

Не забывайте, что синус положителен в первой и второй четвертях, а косинус — в первой и четвертой.

Тригонометрия. Часть 2. Определение координат точек на единичной окружности.
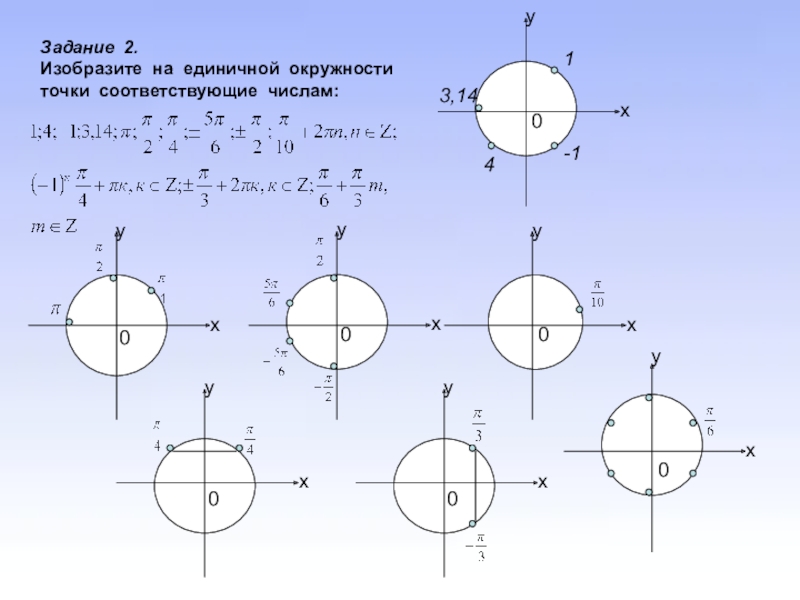
Для углов более 2π отнимайте 2π до получения угла в пределах одного оборота.

Алгебра 10 класс Поворот точки вокруг начала координат Лекция
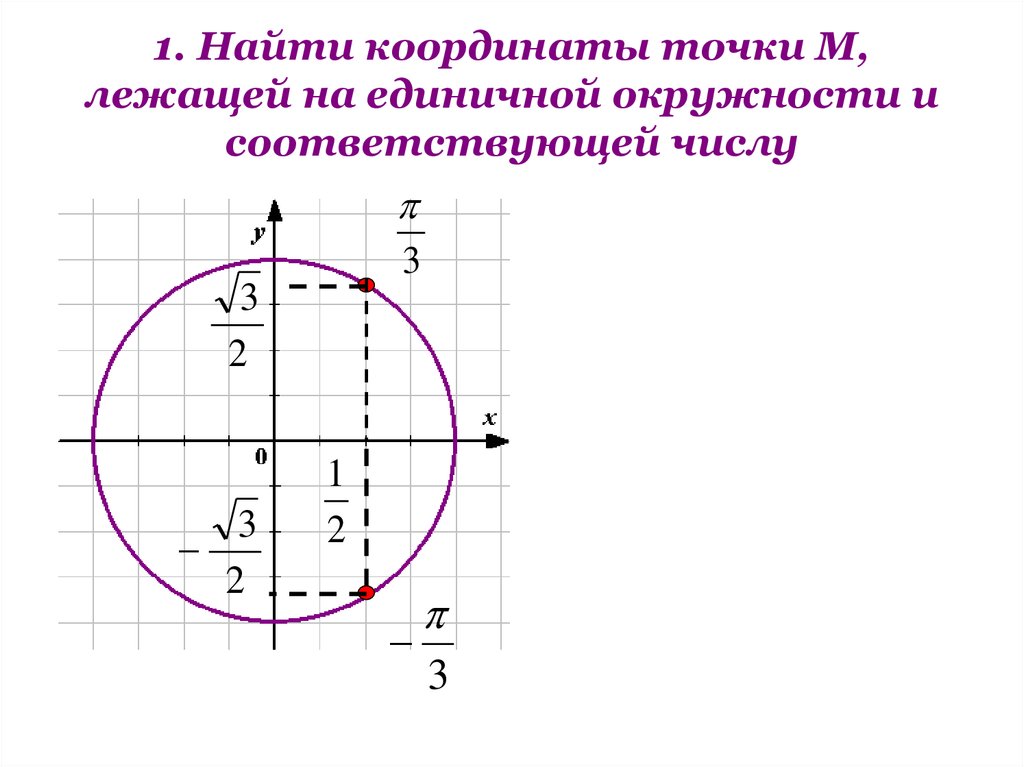
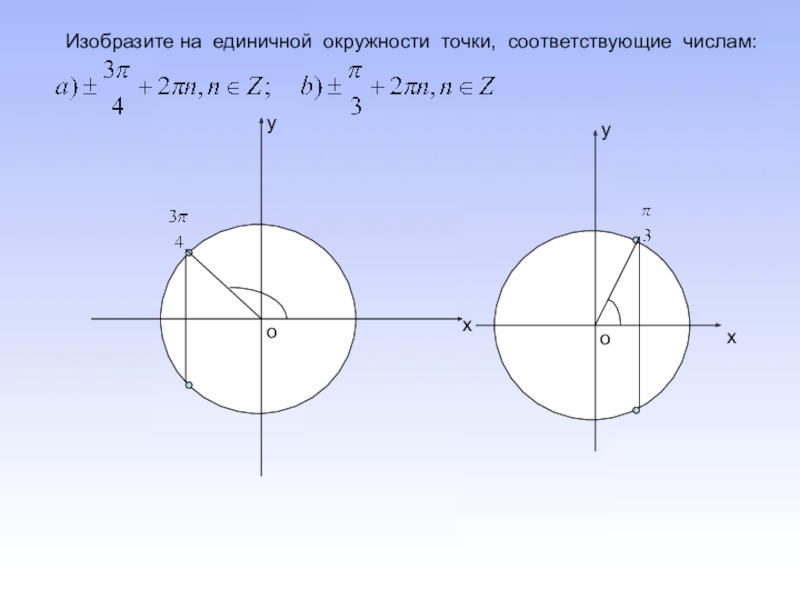
Тренируйтесь на простых задачах: например, найдите координаты точки при θ = π/3 или θ = 5π/6.
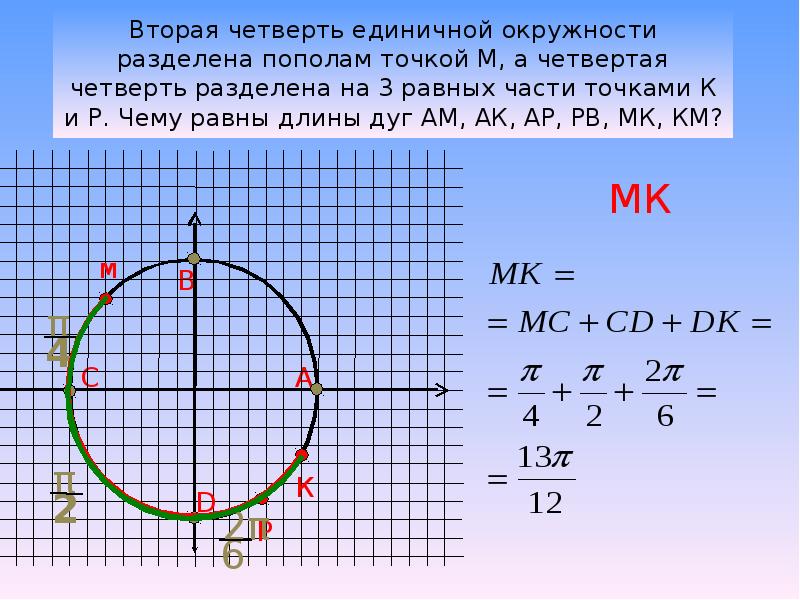
Используйте понятие единичной окружности для понимания сложных тригонометрических функций, таких как тангенс и котангенс.