Пошаговый алгоритм для нахождения точки M на стороне BC треугольника ABC

В данном разделе мы рассмотрим, как правильно отметить точку M на стороне BC треугольника ABC, а также как ее нахождение влияет на свойства треугольника. Вы узнаете, как применить различные геометрические методы для точного и эффективного решения.

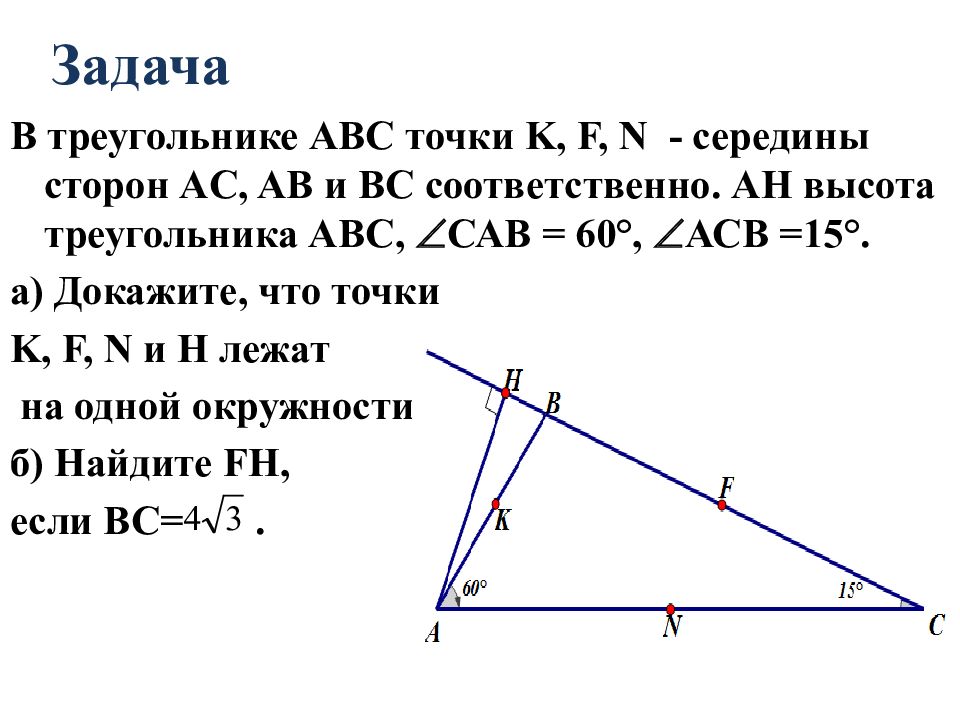
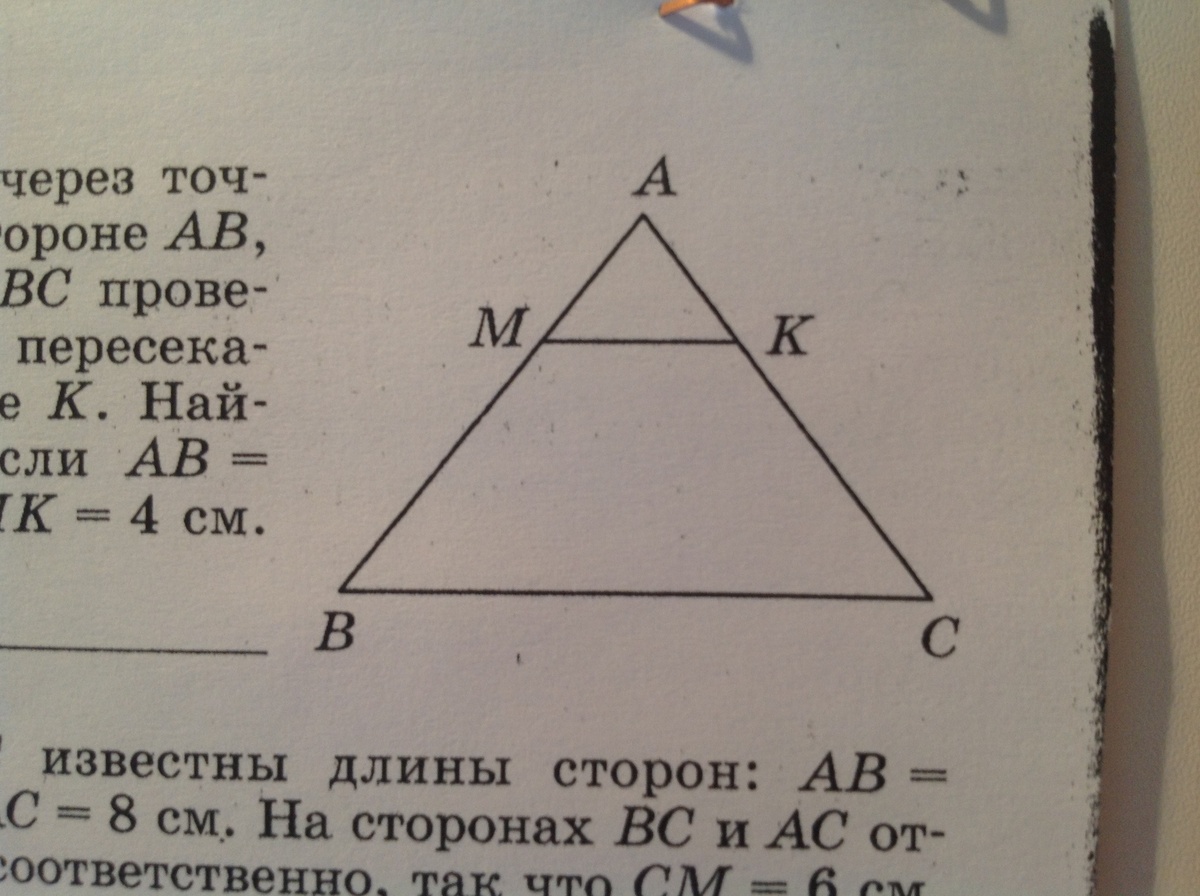
Для точного расположения точки M на стороне BC используйте координатный метод, если известны координаты вершин треугольника.

При нахождении точки M можно использовать пропорциональное деление отрезка, если точка M делит сторону BC в заданном отношении.

Если точка M лежит на середине стороны BC, то она делит треугольник на два равных по площади треугольника.

Использование теоремы о средней линии может помочь в определении точки M, если она располагается на линии, соединяющей середины сторон треугольника.

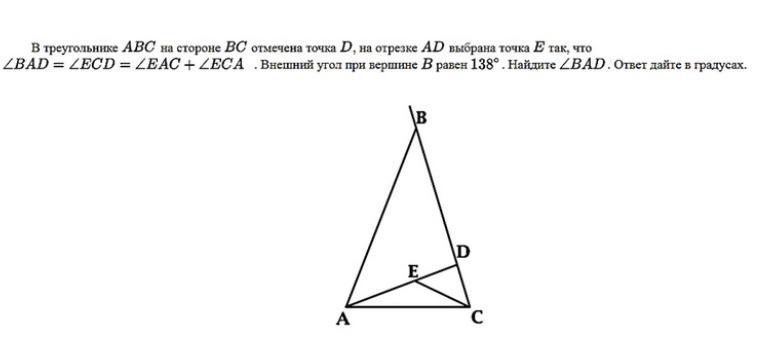
Если точка M является произвольной, важно уточнить ее координаты или соотношение с другими элементами треугольника для дальнейшего анализа.

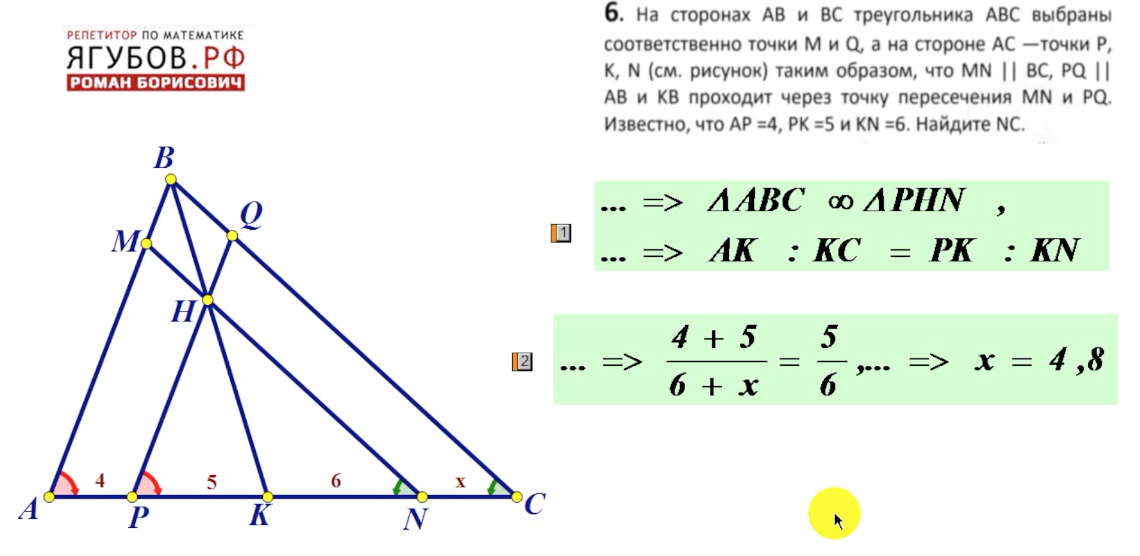
Применение построений с помощью циркуля и линейки позволит вам точно расположить точку M на отрезке BC, особенно в геометрических конструкциях.

При работе с подобными задачами всегда полезно заранее определить возможные геометрические зависимости между точками и сторонами треугольника.

Помимо координатного метода, можно использовать векторный анализ для нахождения точки M, если нужно учесть направление сторон треугольника.

Если точка M является важной для дальнейших построений (например, для нахождения центра масс), учитывайте ее роль в структуре треугольника.

Не забывайте проверять все полученные результаты с помощью дополнительного построения, чтобы убедиться в точности нахождения точки M.