Особенности и свойства медианы, разбивающей треугольник на равные части

Медиана треугольника — это отрезок, соединяющий вершину с серединой противоположной стороны. Этот элемент геометрии обладает интересным свойством: она делит треугольник на два равновеликих треугольника. Это свойство имеет важное значение в различных задачах, включая теоремы и доказательства, а также в практическом применении при решении задач по геометрии. В этой статье мы собрали полезные советы, которые помогут лучше понять, как работает медиана, и как использовать это свойство для решения задач.

Используйте медиану, чтобы разделить треугольник на две равные части для упрощения вычислений.

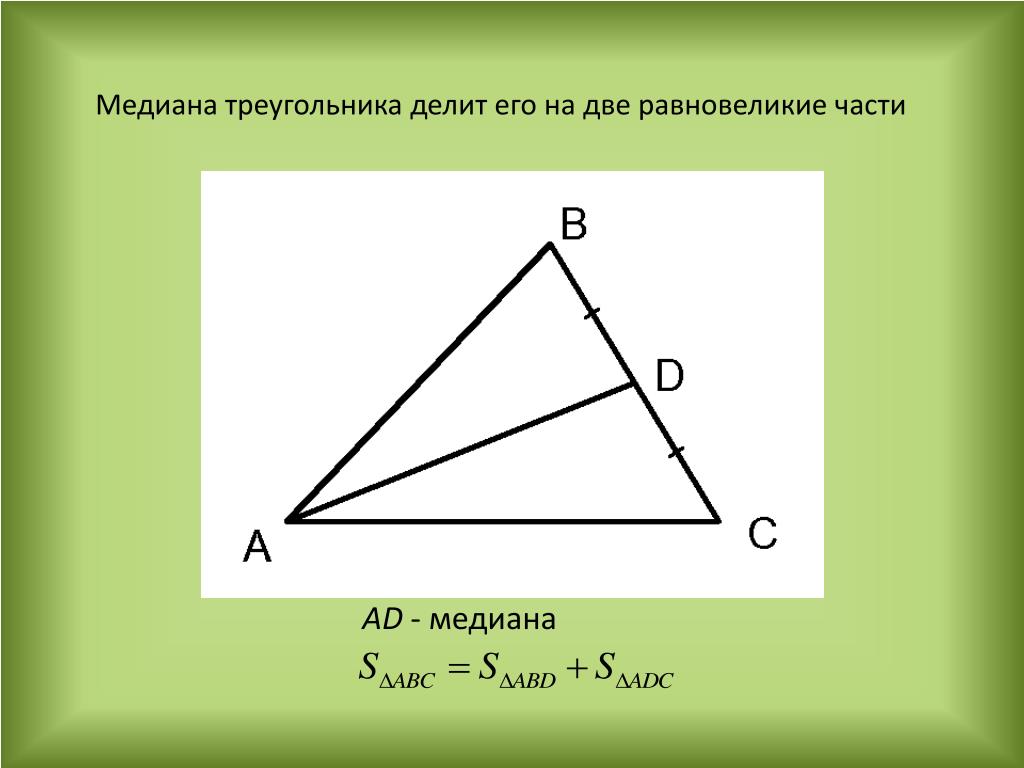
Помните, что медиана всегда делит треугольник на два треугольника одинаковой площади, что полезно для доказательств и вычислений.

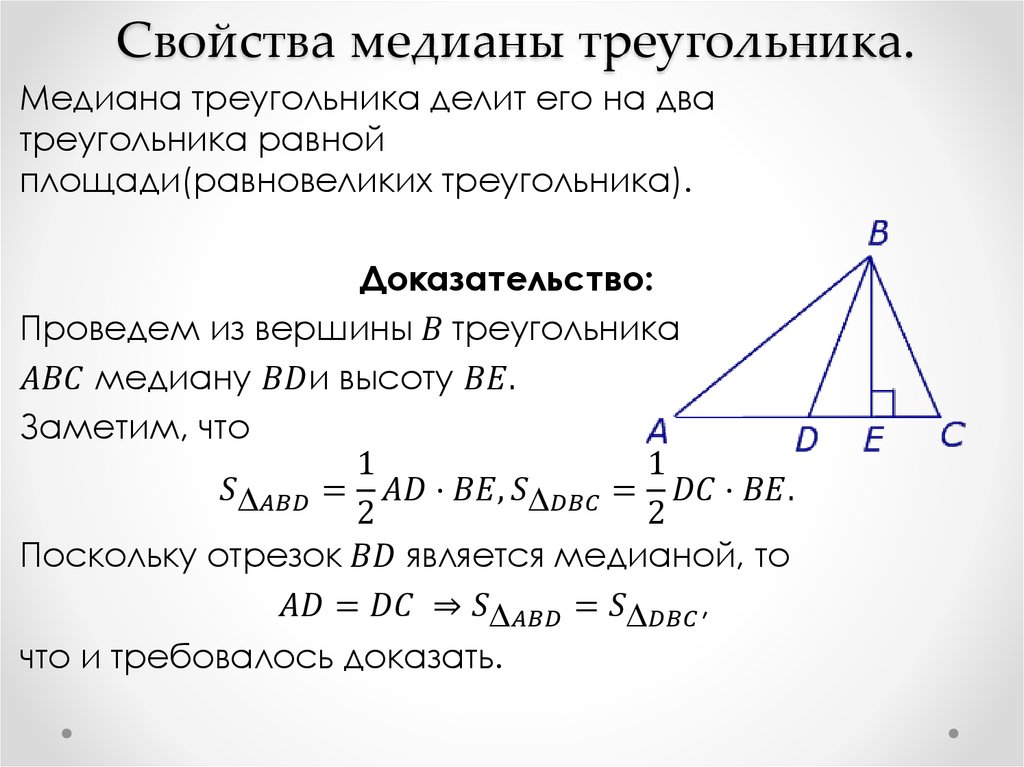
Медиана важна не только в геометрии, но и в инженерных задачах, где нужно учитывать симметрию и равновесие.

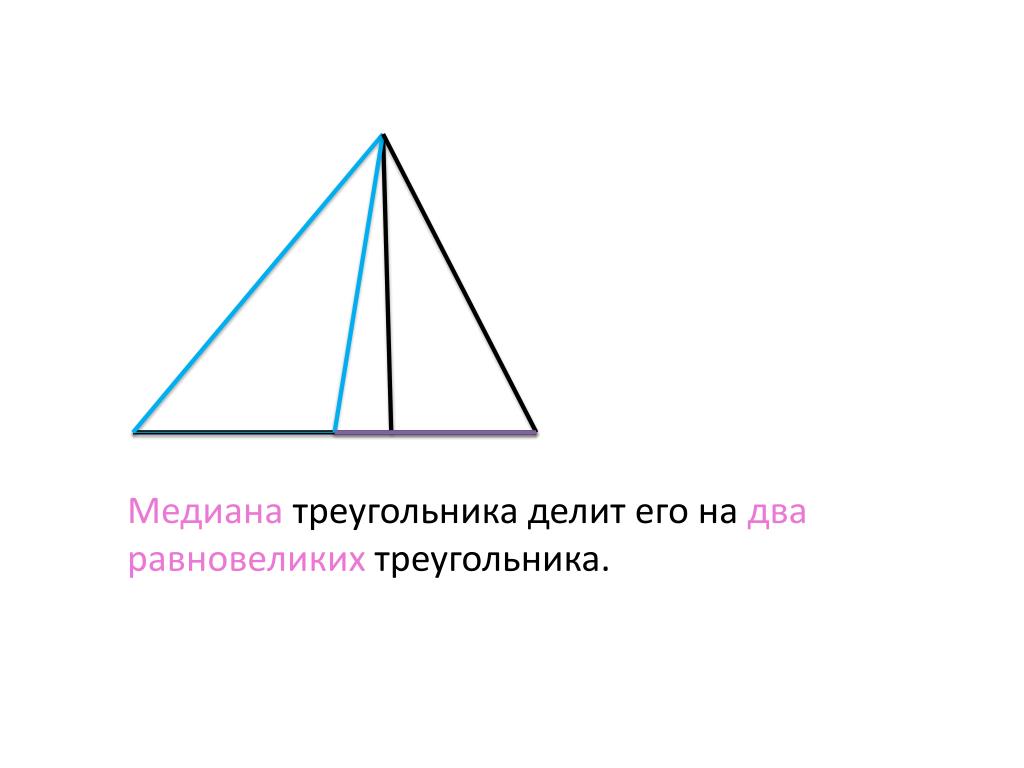
Если в задаче речь идет о симметрии треугольника, медиана всегда будет той линией, которая делит фигуру на две одинаковые части.

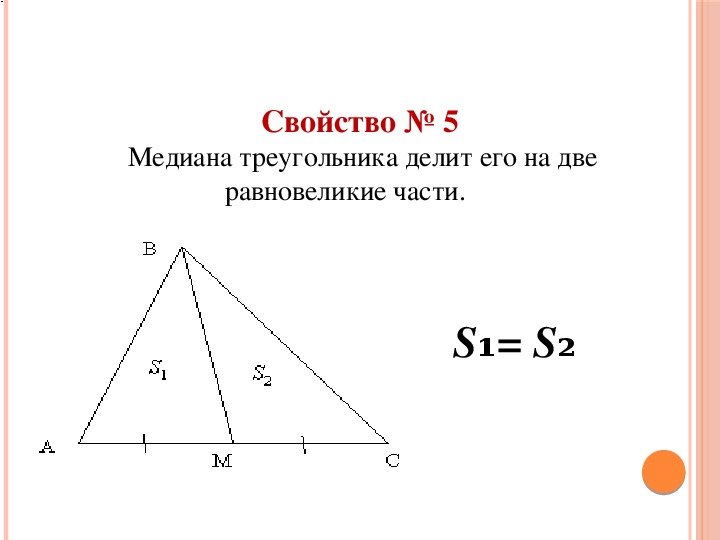
Медиана может быть использована для нахождения центра масс треугольника, что имеет практическое применение в физике.

Не забывайте, что медиана может быть как внутренней, так и внешней в зависимости от типа треугольника.

Для более сложных задач полезно нарисовать все медианы треугольника, чтобы визуально понять его симметрию.

Медиана помогает в решении задач, связанных с нахождением центра тяжести или центроида треугольника.

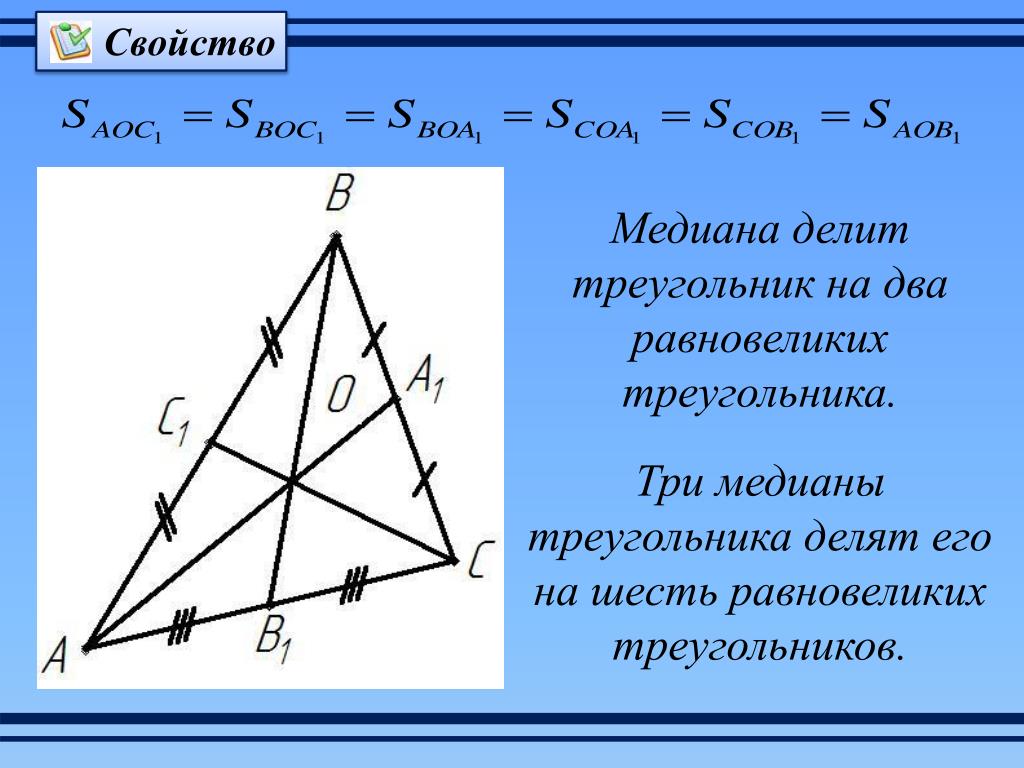
Для доказательства свойств медианы используйте теорему о равновеликих треугольниках, что значительно упростит задачу.

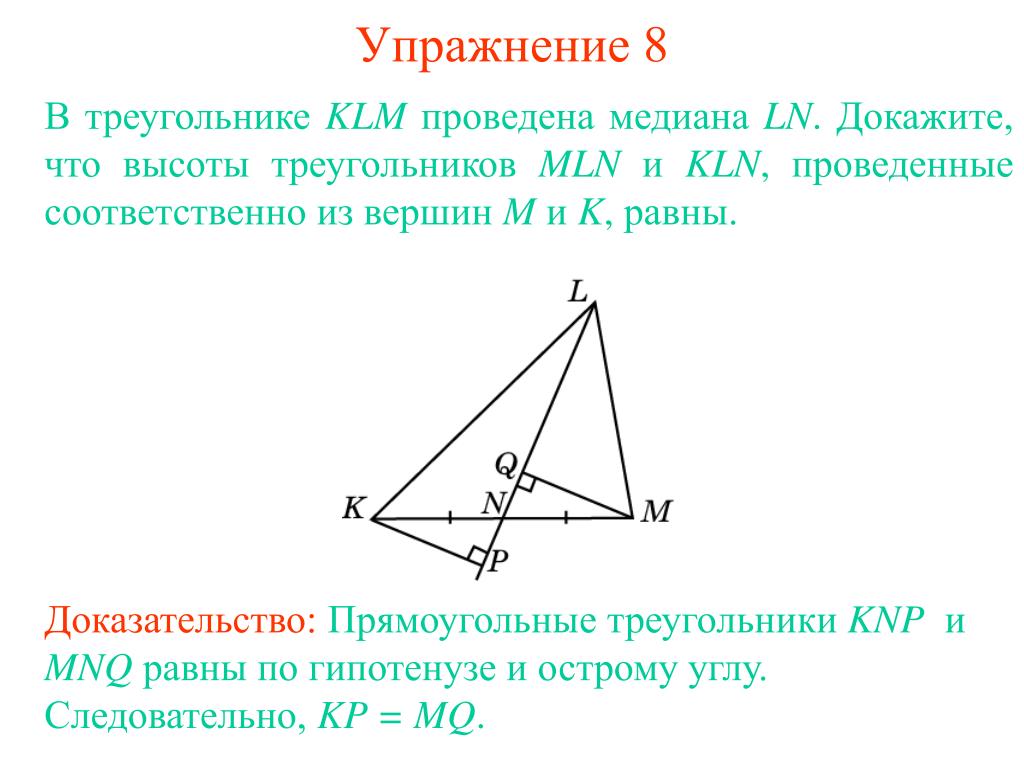
Не бойтесь использовать медиану в нестандартных задачах, это может открыть новые способы решения задач по геометрии.