Как определить и вычислить касательную к графику функции с примерами
Касательная линия к графику функции — это прямая, которая касается графика в одной точке и имеет тот же наклон, что и график функции в этой точке. В этой статье мы разберемся, как правильно определить касательную, используя производные, и научим вас вычислять её уравнение шаг за шагом.
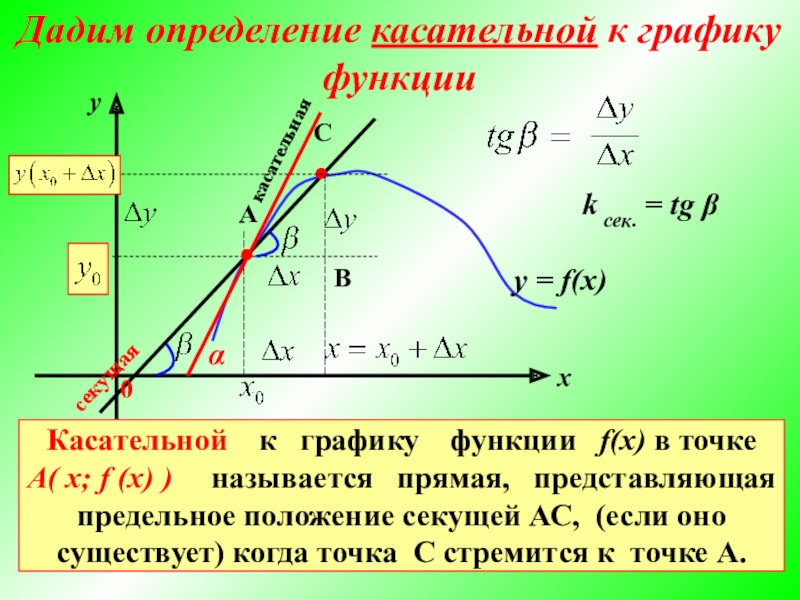

Для определения уравнения касательной необходимо сначала найти производную функции в точке касания.

Уравнения касательной и нормали к графику функции (часть 1). Высшая математика.
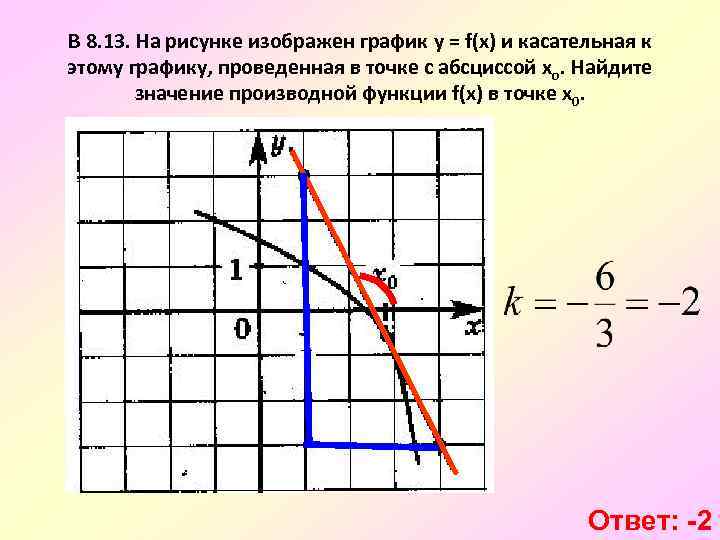
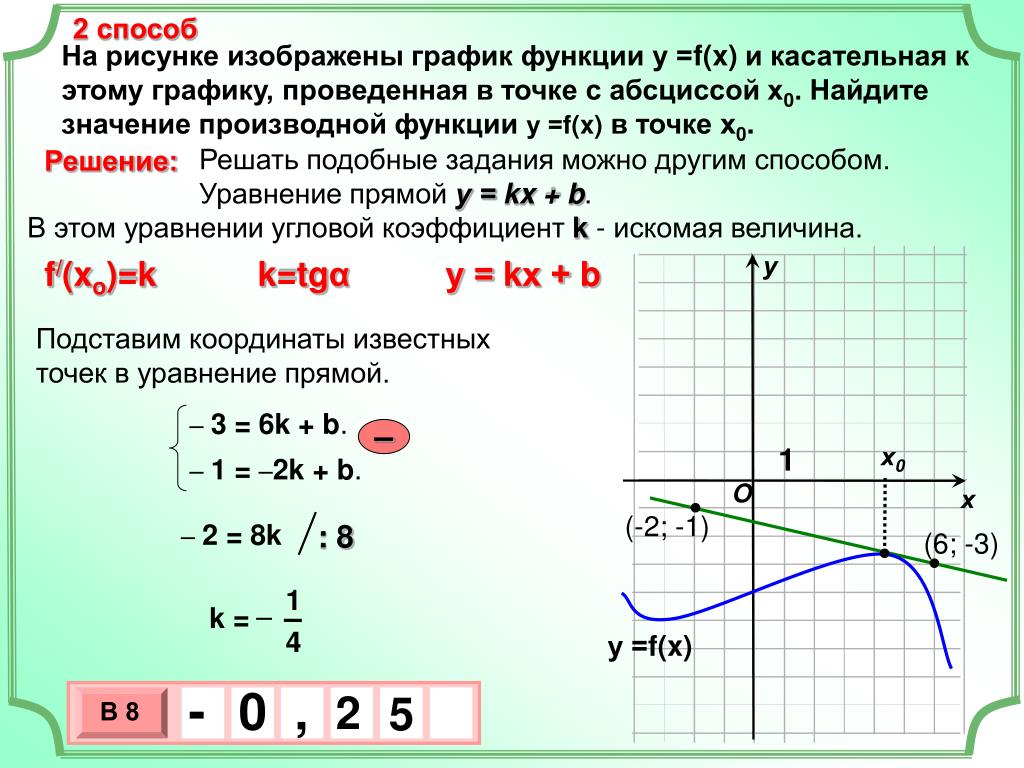
Не забудьте, что производная функции в точке касания равна угловому коэффициенту касательной к графику функции.

Нахождение тангенса угла наклона касательной к графику функции. Угол наклона касательной к графику
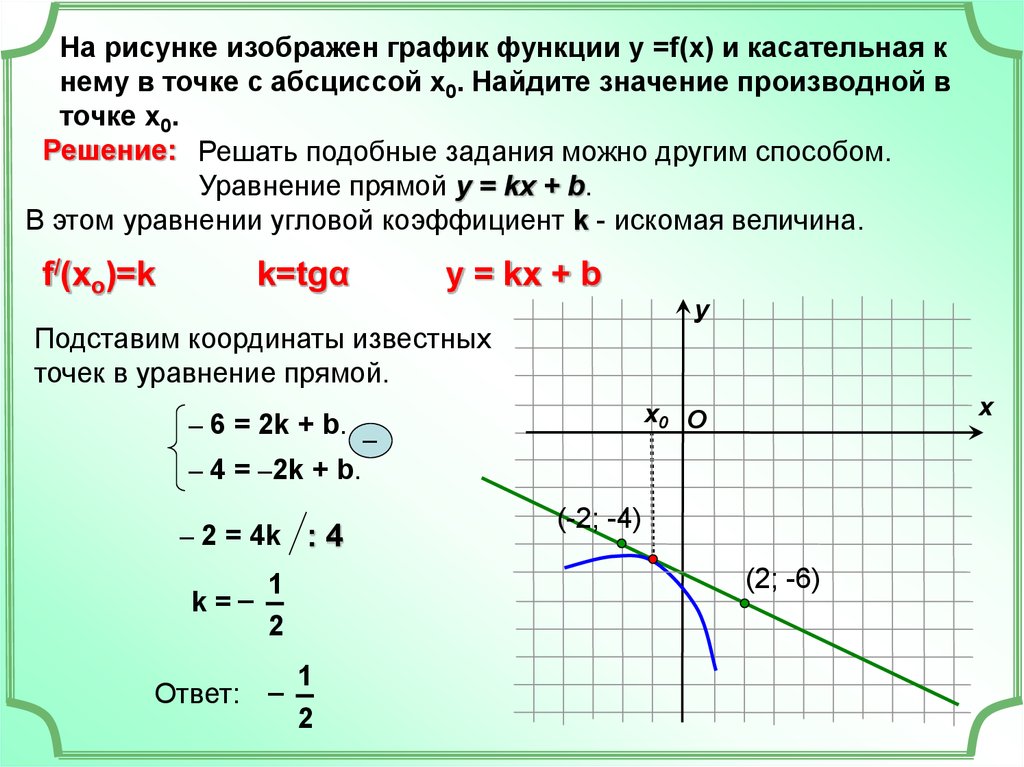
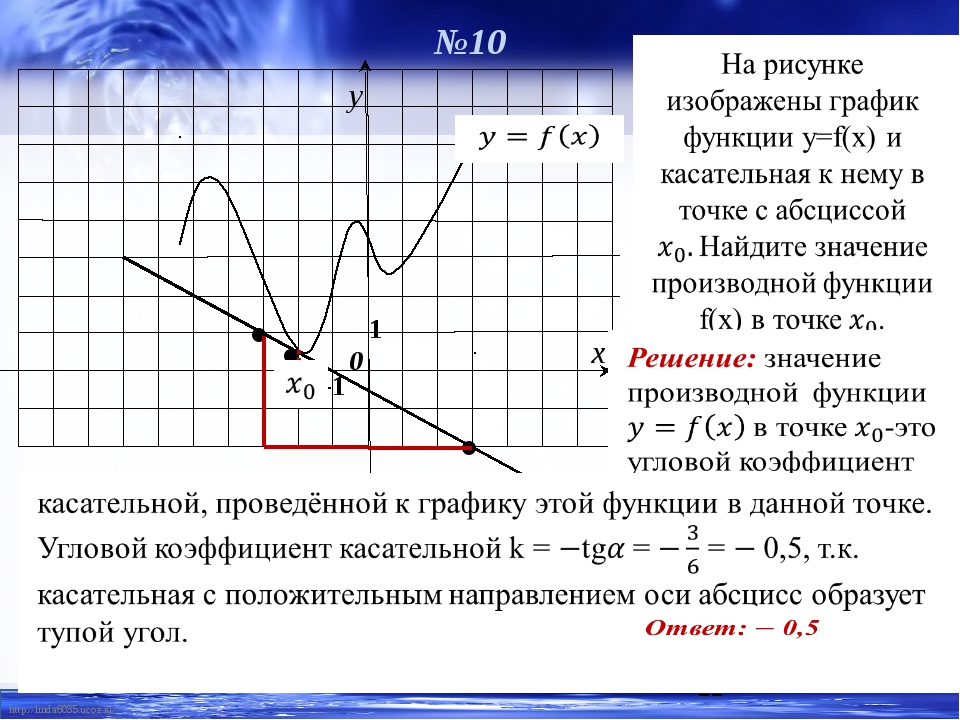
Чтобы найти точку касания, необходимо подставить значение аргумента в исходную функцию.

Геометрический смысл производной - Касательная

Для нахождения уравнения касательной используйте формулу: y - y₁ = f(x₀)(x - x₀), где (x₀, y₁) — точка касания, f(x₀) — производная в этой точке.

Общая схема исследования функции и построение ее графика

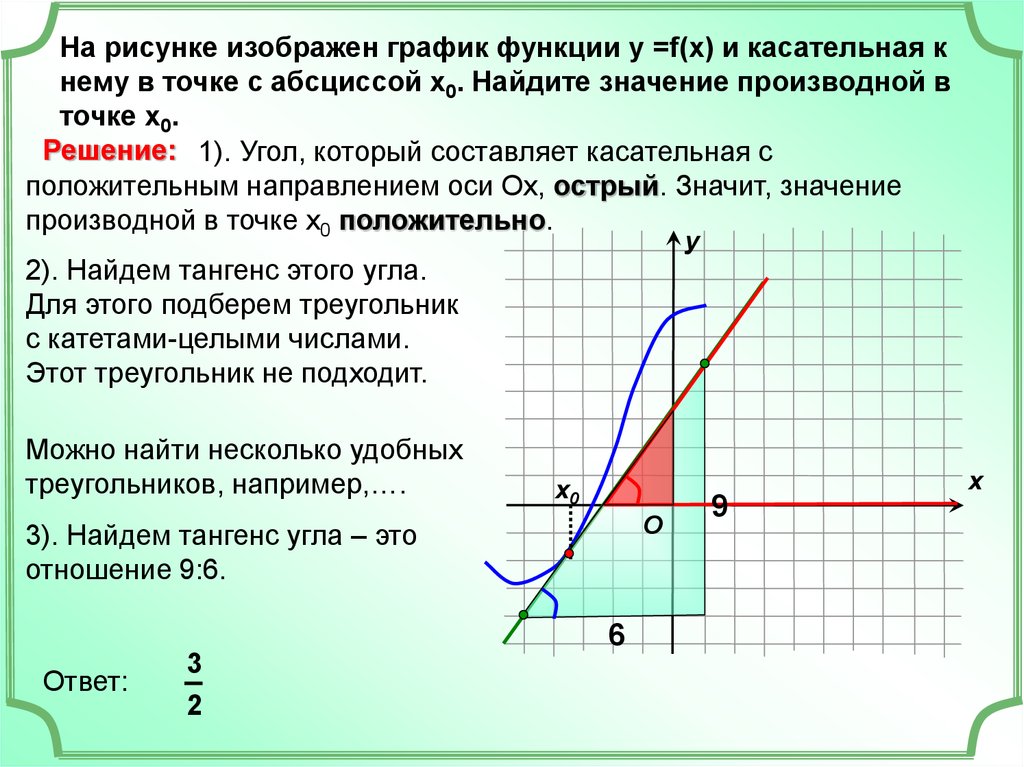
Не забудьте про единичные меры: если график задан в пикселях или других единицах, корректно определяйте их перед расчетами.
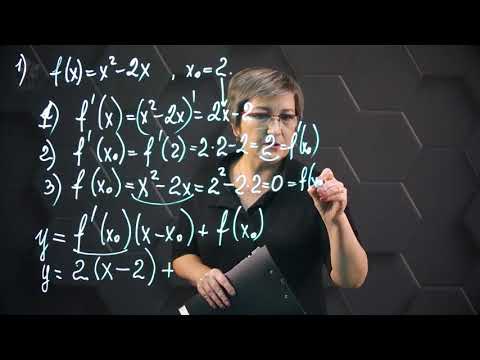
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.

При вычислениях всегда проверяйте, существует ли производная функции в точке касания.

Если функция имеет разрыв или вертикальную асимптотику в точке касания, касательная в этой точке не существует.
Использование графиков и численных методов поможет вам наглядно увидеть, как изменяется наклон касательной по мере изменения точки касания.

10 класс, 43 урок, Уравнение касательной к графику функции

Для точности расчетов рекомендуется использовать калькуляторы или программное обеспечение для нахождения производных и построения графиков.

Математика без Ху%!ни. Уравнение касательной.


Проверяйте результаты на практике, используя касательную для приближенного вычисления значений функции вблизи точки касания.
