Методы вычисления углов в прямоугольном треугольнике при известности сторон
На этой странице вы найдете советы и примеры, которые помогут вам правильно вычислить угол в прямоугольном треугольнике, если известны его стороны. Это полезное руководство для студентов и всех, кто изучает основы тригонометрии и геометрии.

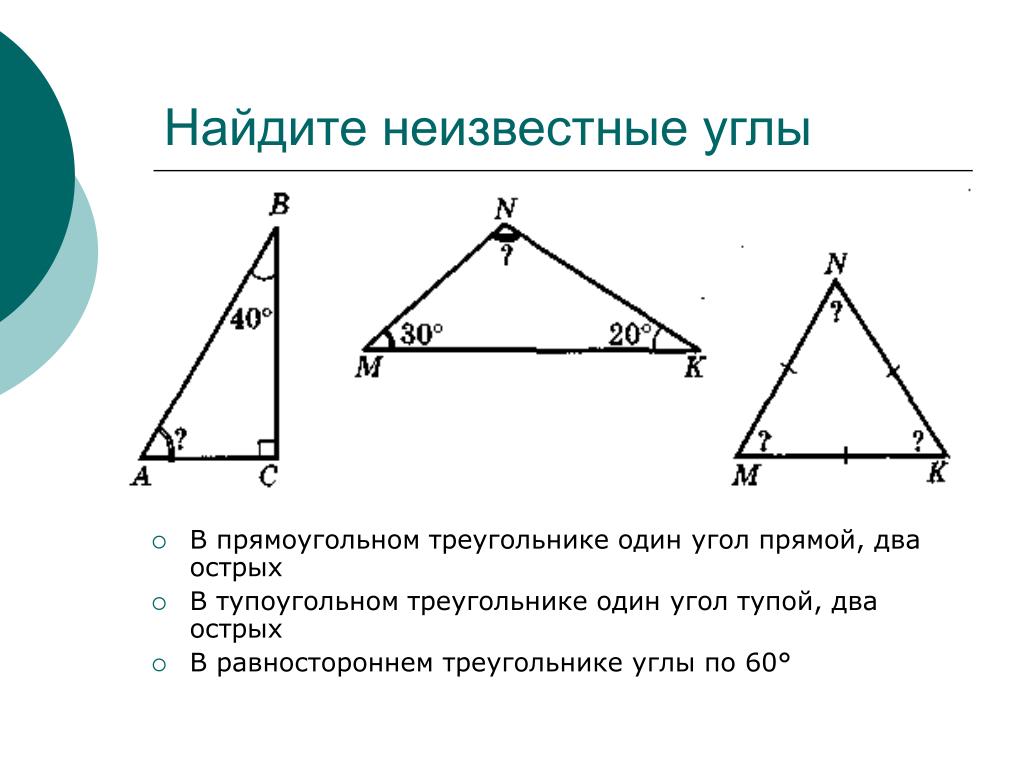
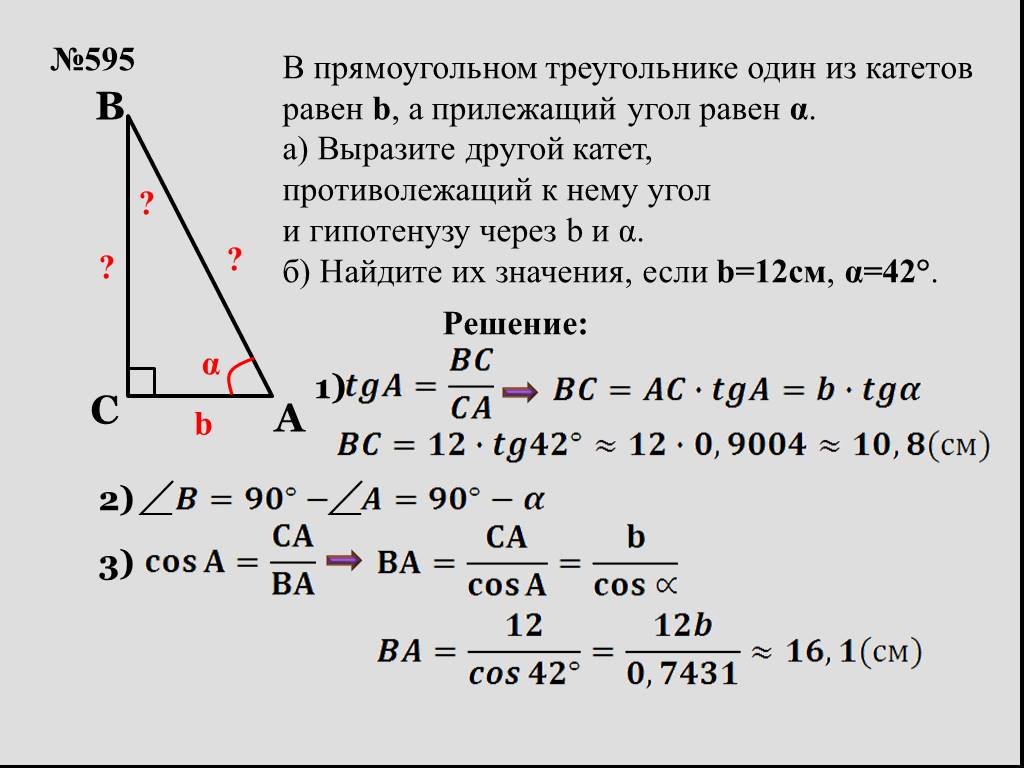
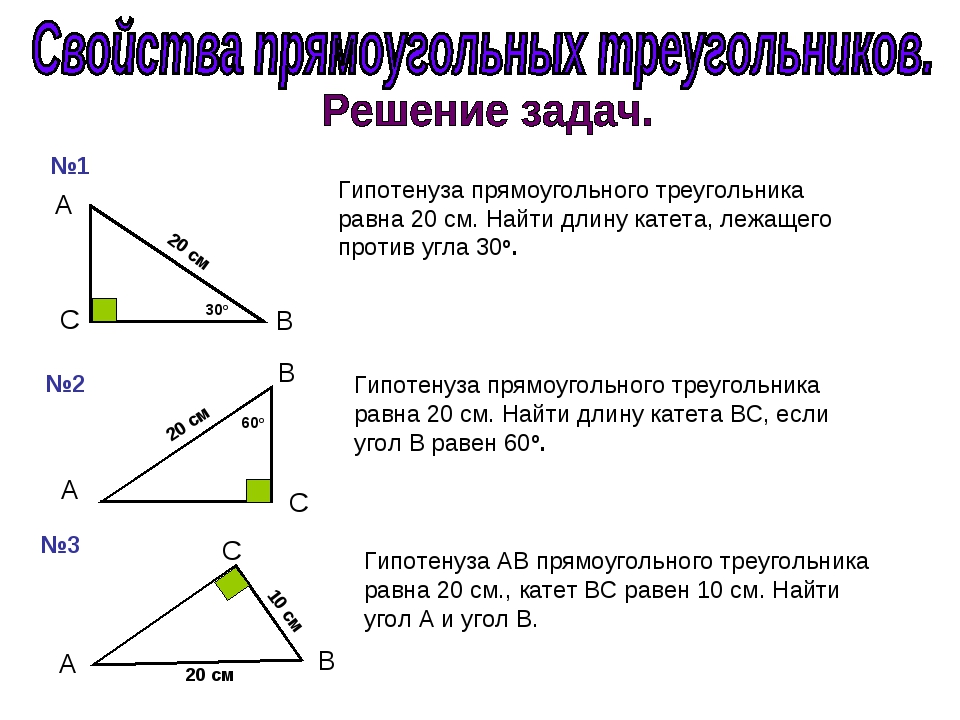
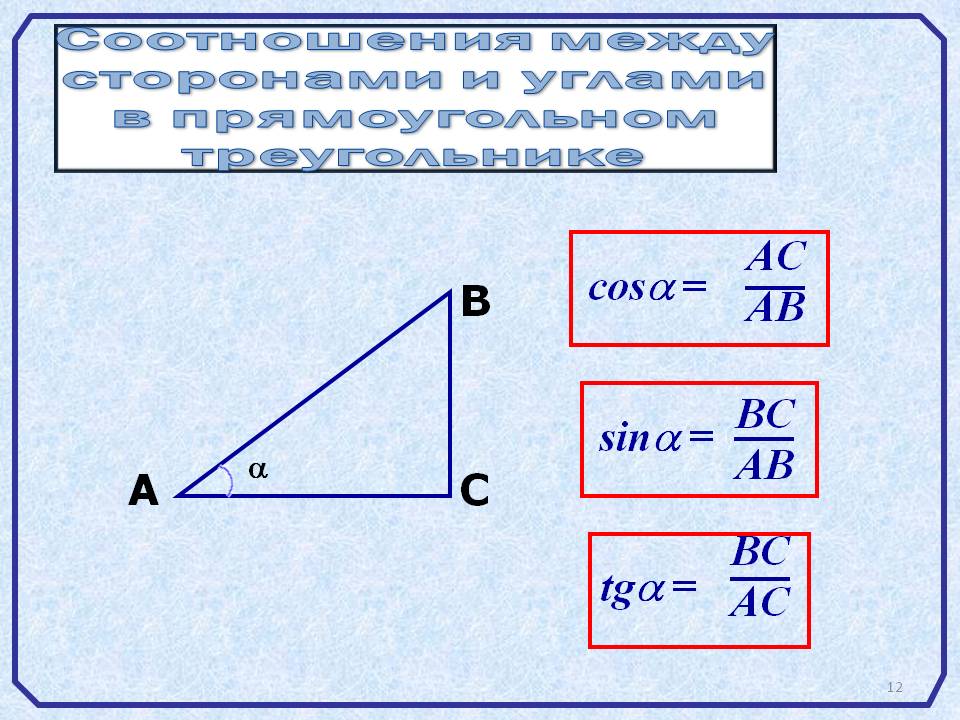
Для вычисления угла прямоугольного треугольника, зная его стороны, можно использовать формулы тригонометрии, например, синус, косинус или тангенс.
Нахождение стороны прямоугольного треугольника

Если известны длины катетов, угол можно вычислить через тангенс: tg(угол) = противолежащий катет / прилежащий катет.
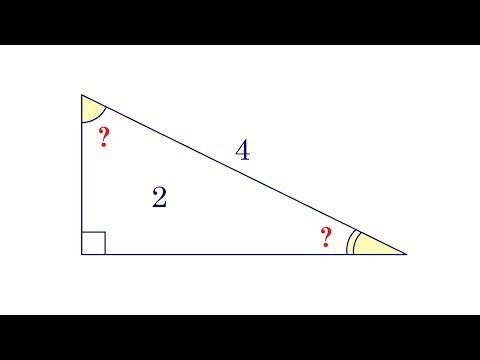
Только 1% может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬ
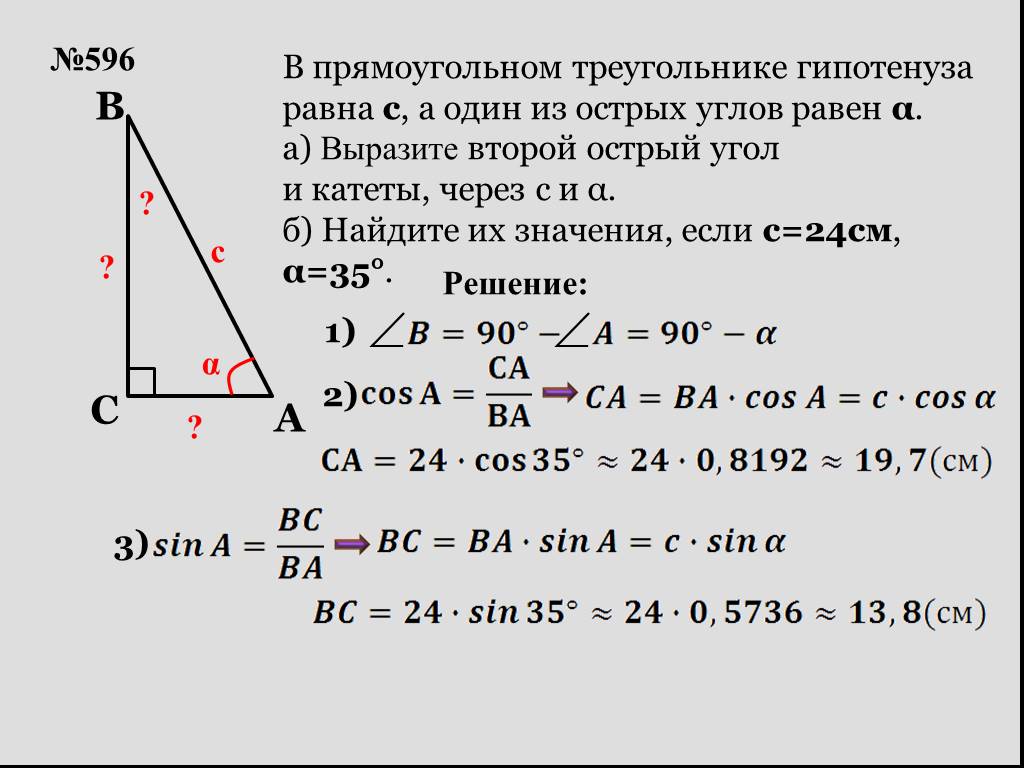
Если известен гипотенуза и один из катетов, используйте косинус или синус для нахождения угла: cos(угол) = прилежащий катет / гипотенуза.

Почти никто не решил ➜ Найдите сторону треугольника

Для вычисления угла через синус используйте формулу: sin(угол) = противолежащий катет / гипотенуза.

Как рассчитать лестницу на второй этаж

Для точности вычислений важно учитывать, что угол в прямоугольном треугольнике всегда будет меньше 90°, если треугольник не является равнобедренным.

Свойства прямоугольного треугольника. Практическая часть. 7 класс.
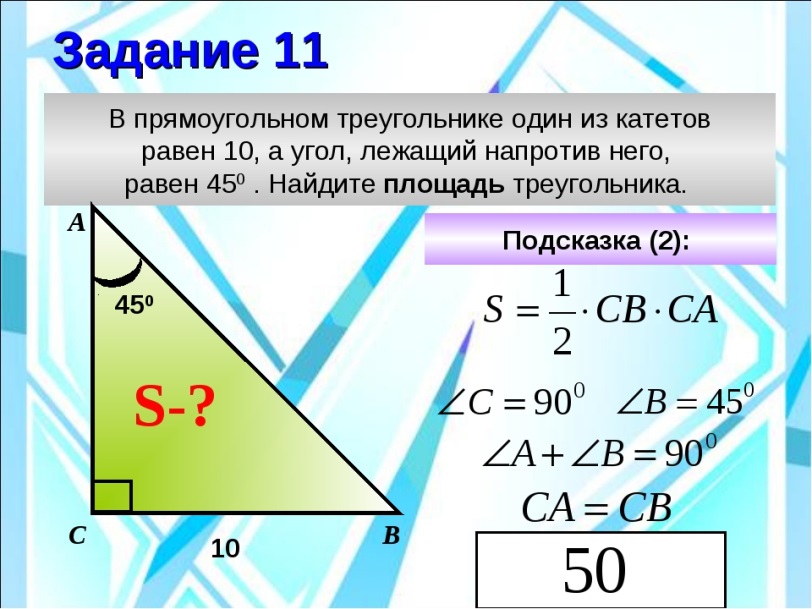
Используйте калькулятор или таблицы тригонометрических функций, чтобы ускорить процесс нахождения углов в прямоугольных треугольниках.

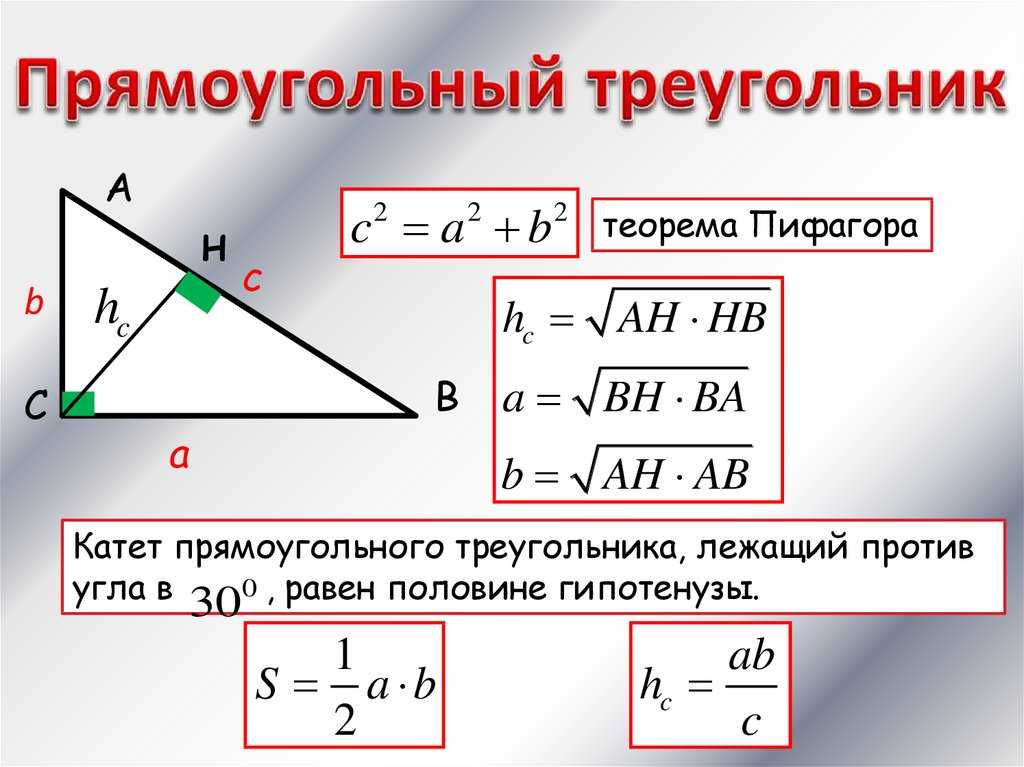
В случае, если известны все три стороны треугольника, используйте теорему Пифагора для проверки правильности вычислений углов.
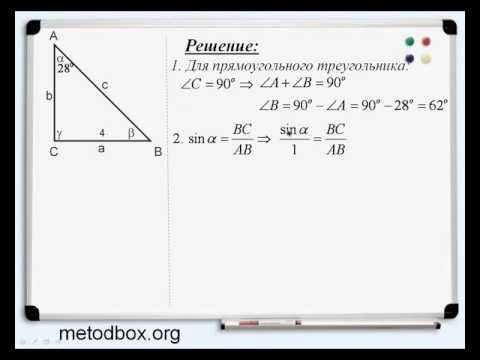
Решение прямоугольных треугольников
Для более сложных случаев можно использовать аркфункции: arcsin, arccos, arctan для вычисления углов, если известны отношения сторон.

Классный способ для разметки любого угла без транспортира.
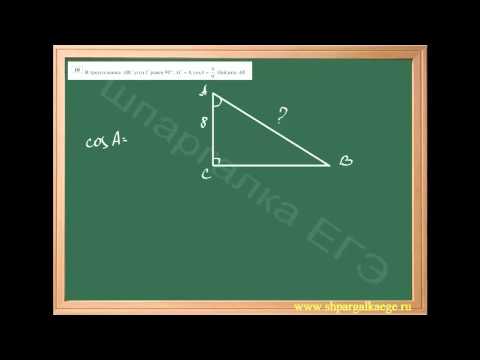
Определение длины гипотенузы
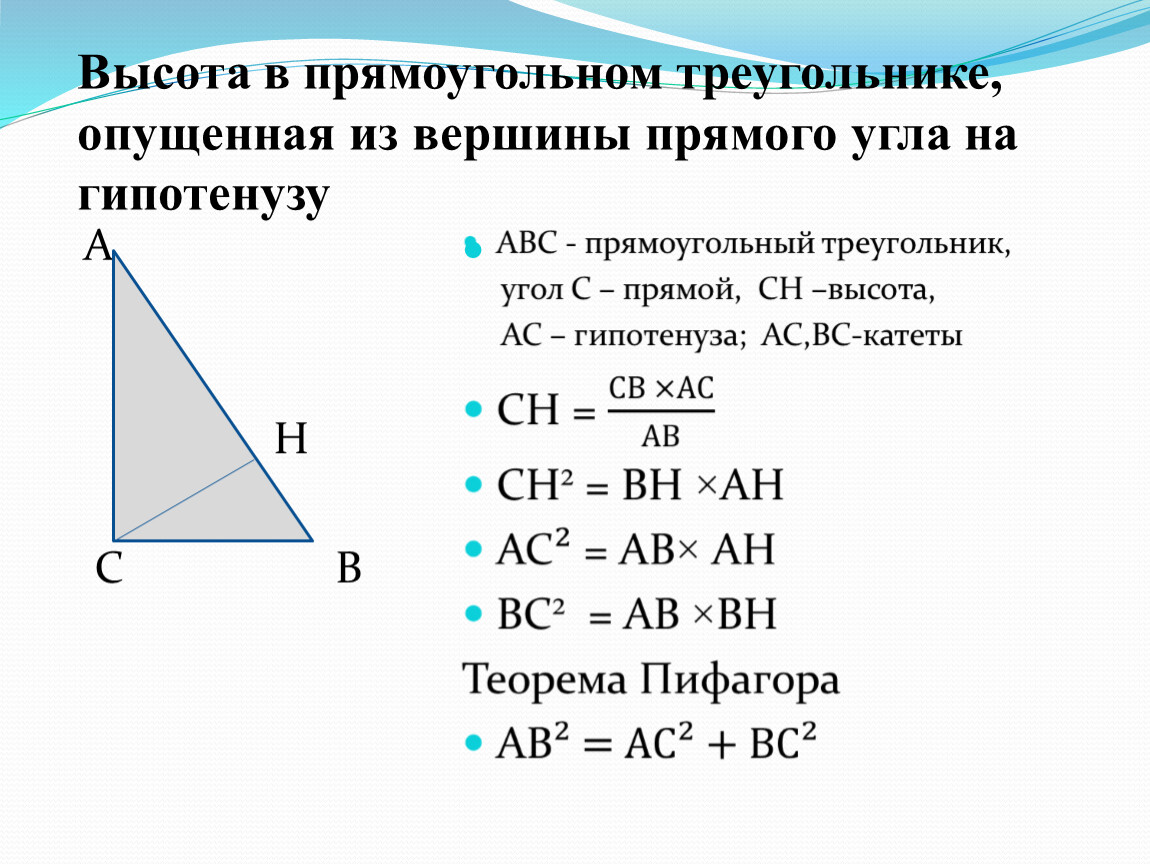
Не забывайте, что углы в треугольнике всегда суммируются до 180°, и если один угол прямой, то сумма других двух углов будет 90°.

Найдите углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18
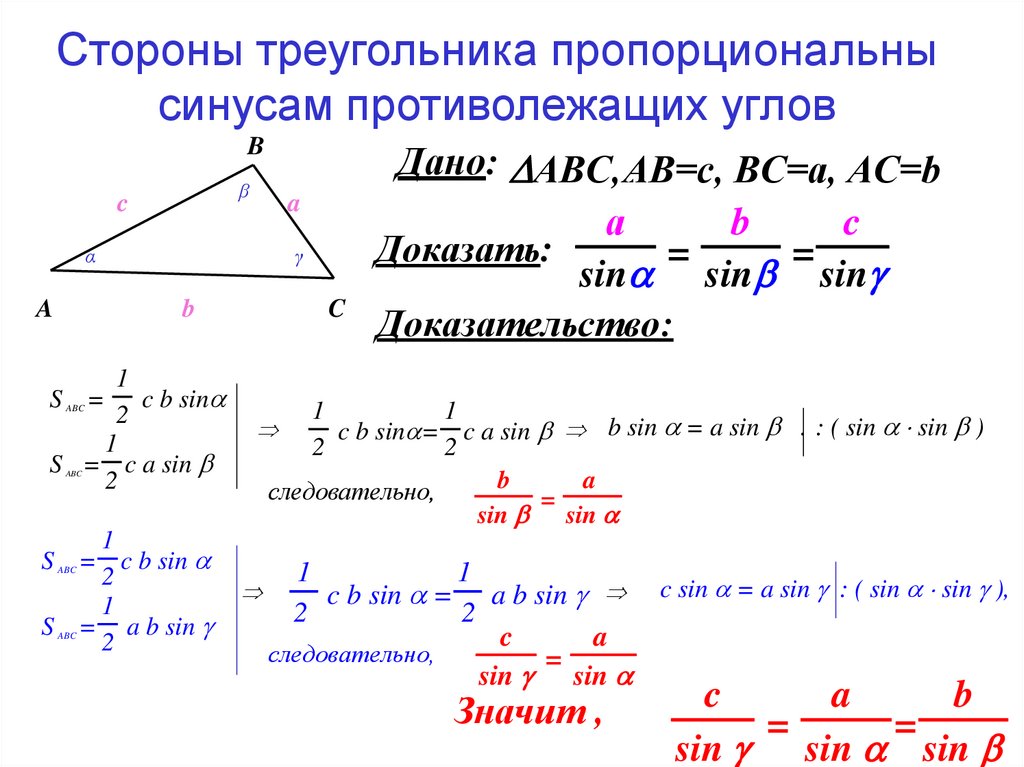
Регулярно практикуйтесь в вычислениях углов, чтобы быстрее ориентироваться в математических задачах и повысить свою уверенность в решении задач по геометрии.