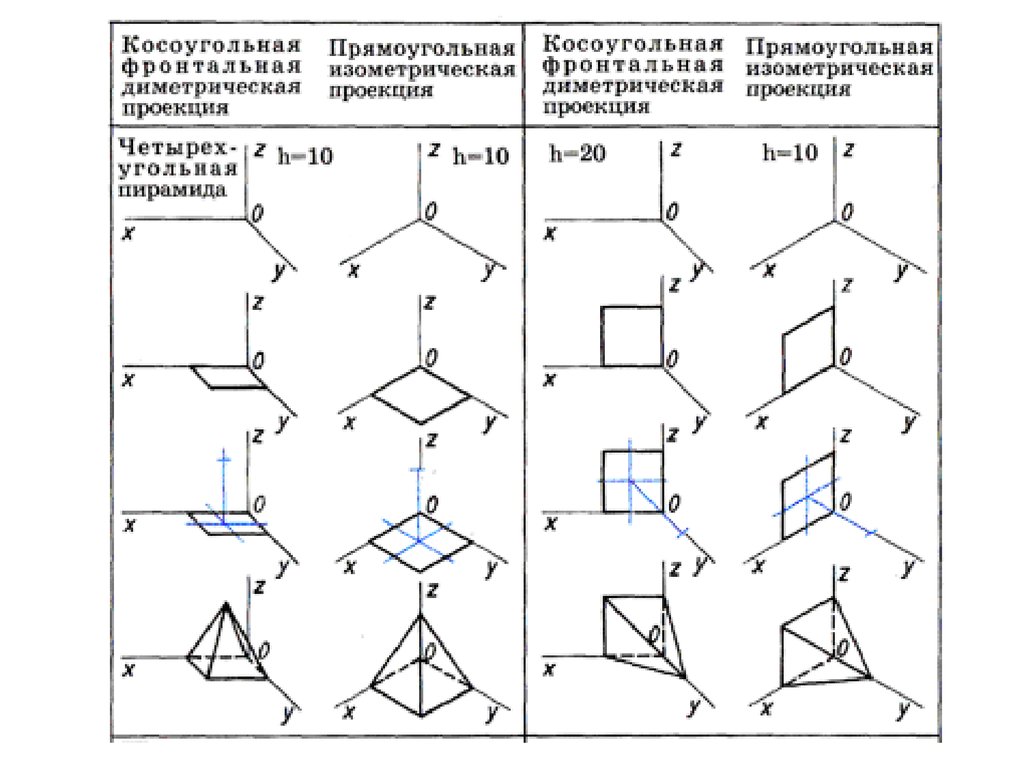
Как правильно применять изометрическую проекцию для треугольников в графическом дизайне
Изометрическая проекция — это метод отображения трехмерных объектов на двумерной плоскости, который позволяет создать иллюзию объема без перспективных искажений. Особенно полезен этот метод при изображении геометрических форм, таких как треугольники, и широко применяется в архитектуре, дизайне и компьютерной графике. На этой странице вы найдете советы по правильному построению и использованию изометрической проекции для треугольников, а также фотографии, которые помогут вам лучше понять принцип этого визуального метода.
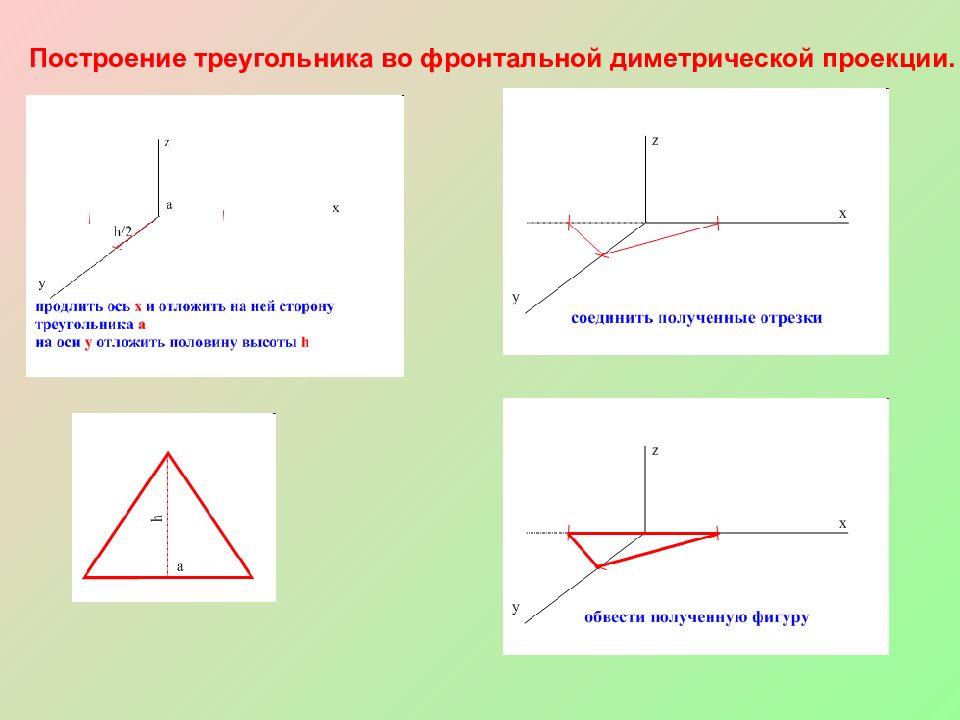
Для корректного отображения треугольников в изометрической проекции используйте одинаковый угол наклона всех осей (обычно 30 градусов) для сохранения пропорций.

Построение треугольника в трёх проекциях
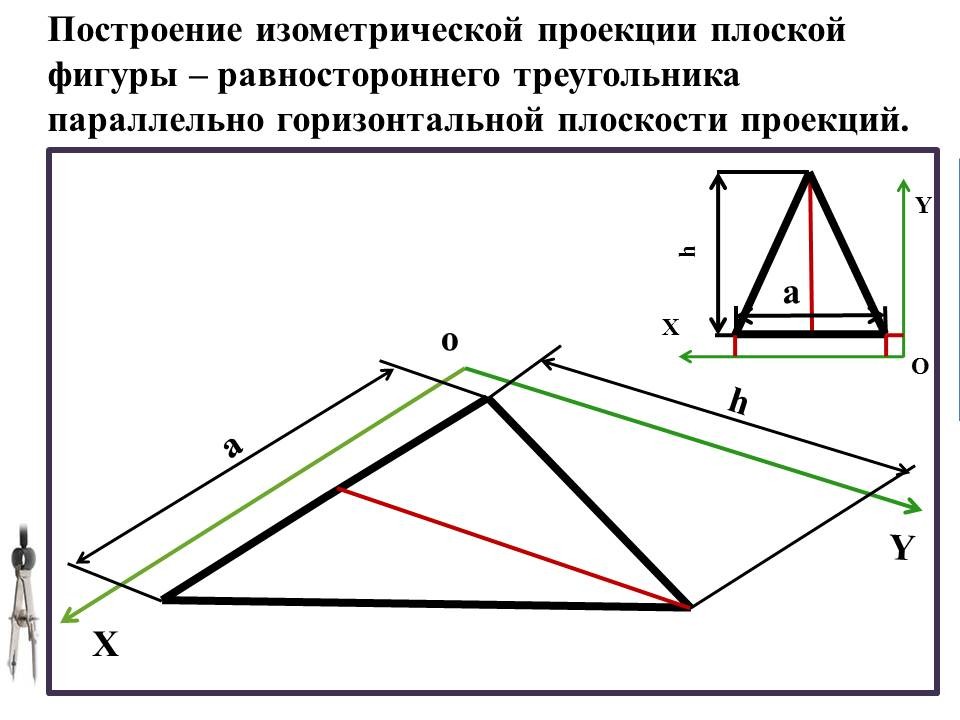
Перед тем как начать рисовать, определитесь с тем, какой вид треугольника вы хотите изобразить: равнобедренный, равносторонний или скалярный.

Построение аксонометрии модели
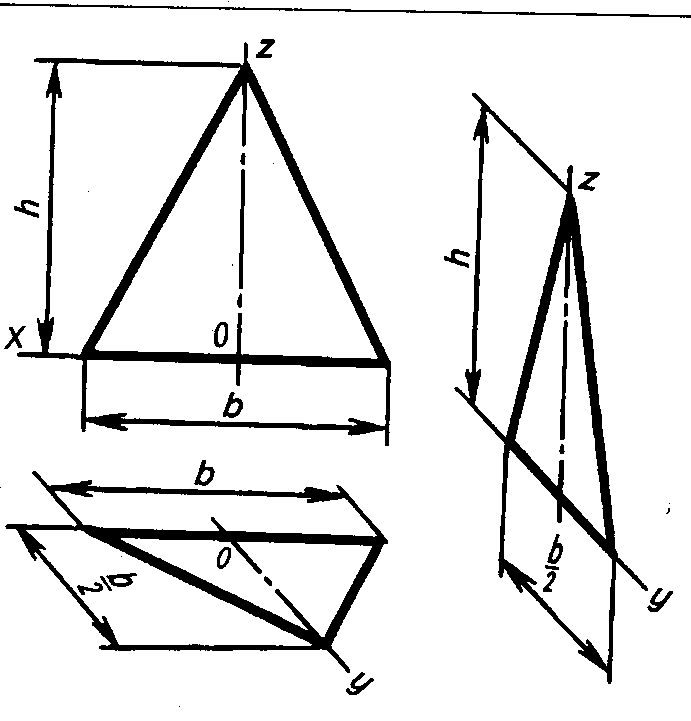
Если необходимо создать более сложные изометрические изображения, начните с построения базовых форм, таких как прямоугольники и квадраты, а затем добавляйте треугольники.

Треугольная призма. Ортогональные и изометрическая проекции. Урок 10.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)
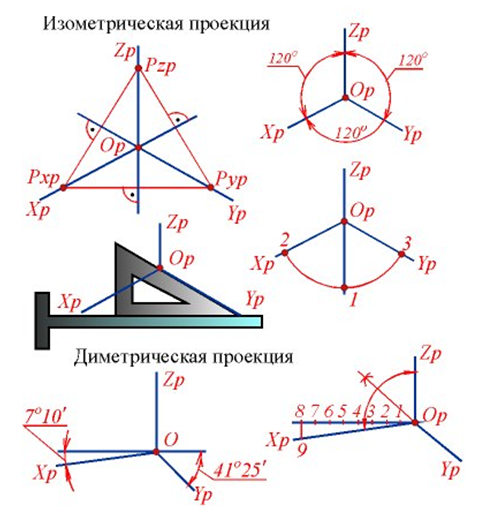
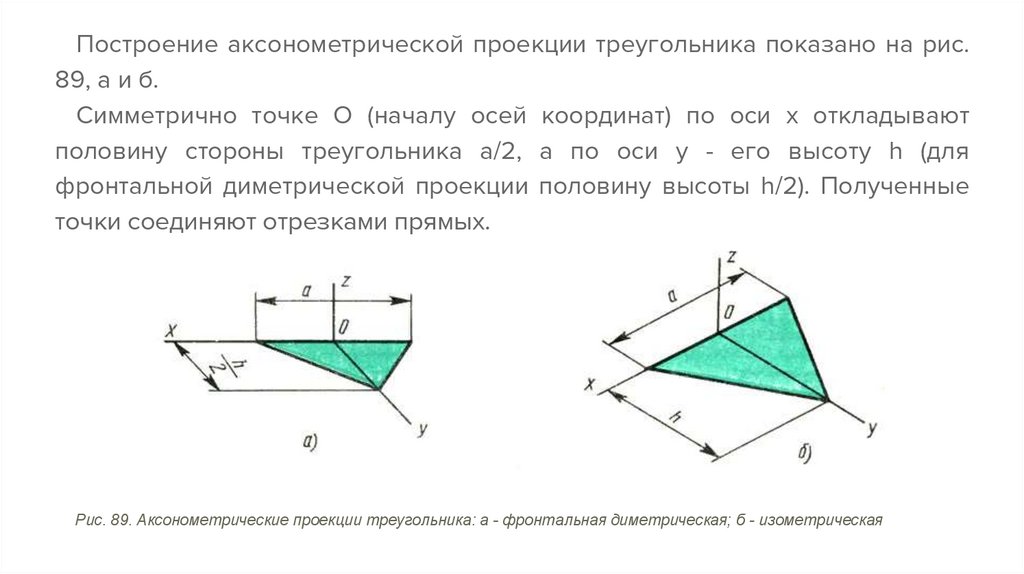
Для точности линии треугольника в изометрии стоит использовать сетку с изометрическими координатами, чтобы избежать ошибок в углах и расстояниях.

Треугольная пирамида. Ортогональные и изометрическая likerkacinema.ru22.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)
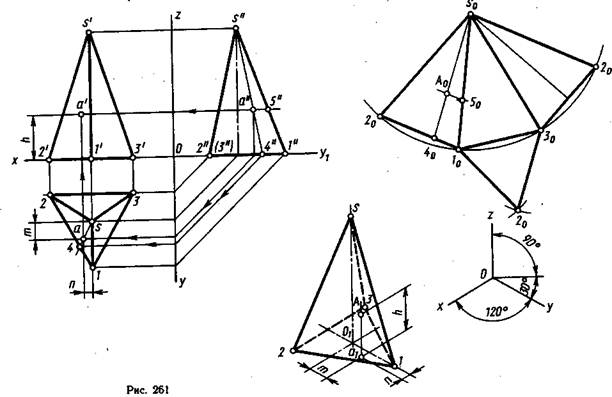
Для улучшения восприятия изображения используйте мягкие тени и световые эффекты, чтобы подчеркнуть объемность треугольников в изометрической проекции.

Треугольник в изометрии. ПлоскостьП1
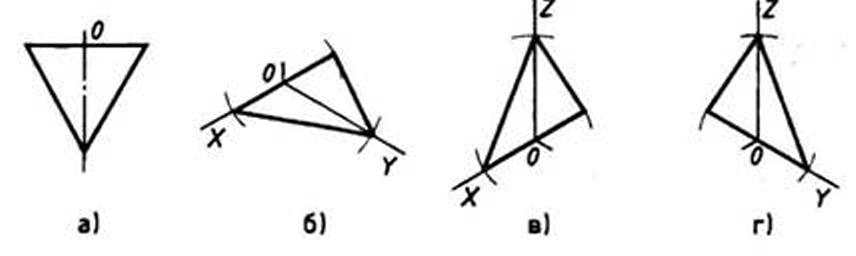
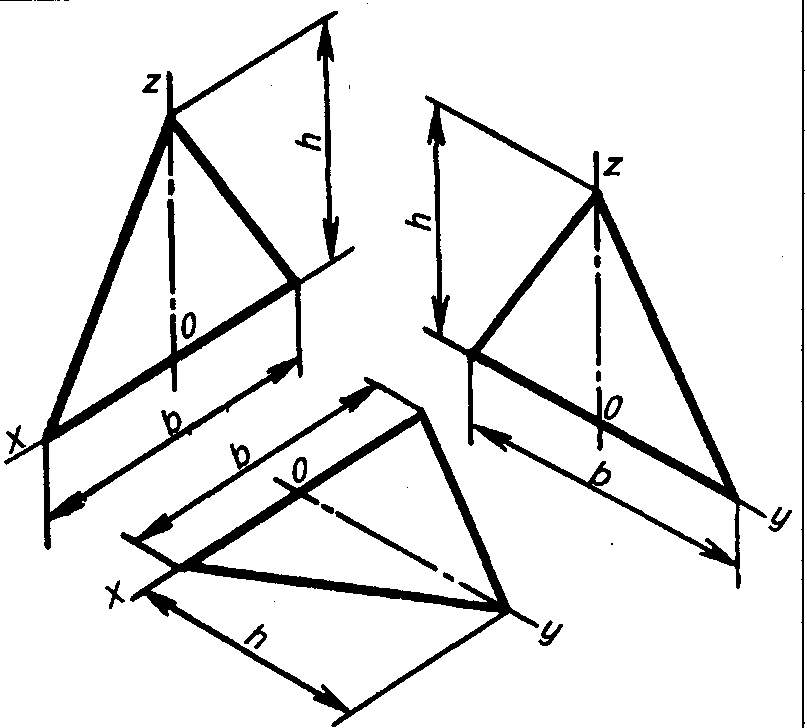
Обратите внимание на симметрию при рисовании треугольников, особенно если вы хотите, чтобы их стороны были равными по длине и углы — одинаковыми.
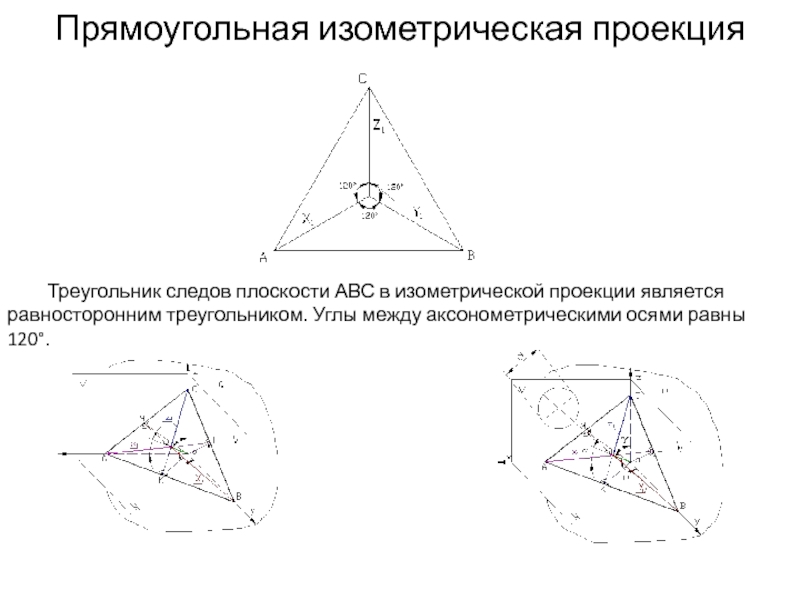
Используйте графические редакторы, такие как Adobe Illustrator или AutoCAD, для более точного и легкого создания изометрических изображений треугольников.
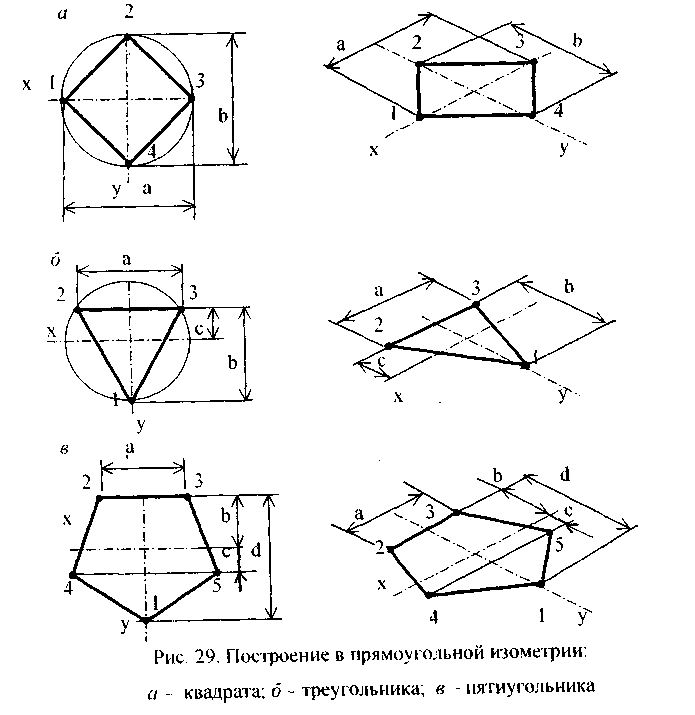
Практикуйте построение треугольников в изометрии вручную с помощью линейки и угольников, чтобы лучше понять пространственные пропорции.
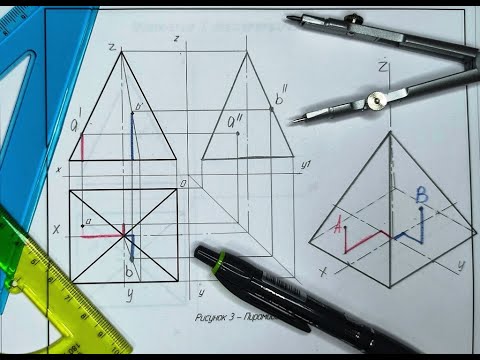
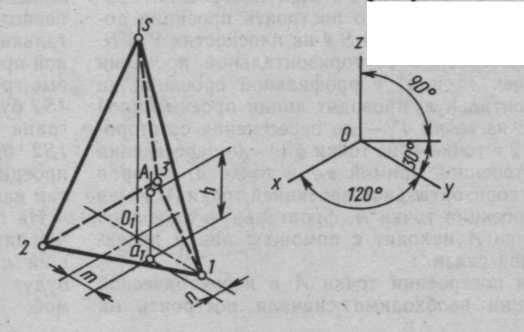
ПИРАМИДА в ИЗОМЕТРИИ
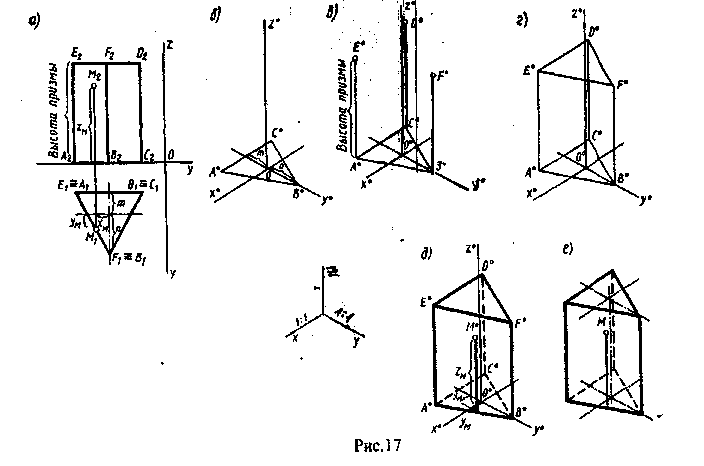
Для сложных изометрических композиций старайтесь избегать перегрузки изображения, делая треугольники частью более крупных геометрических фигур.
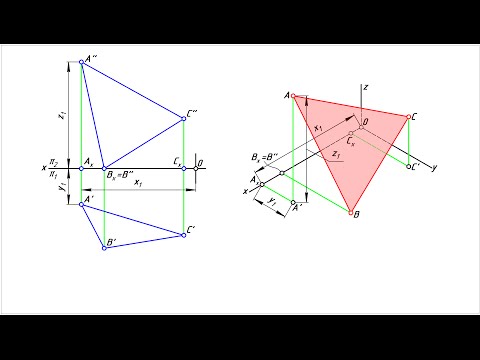
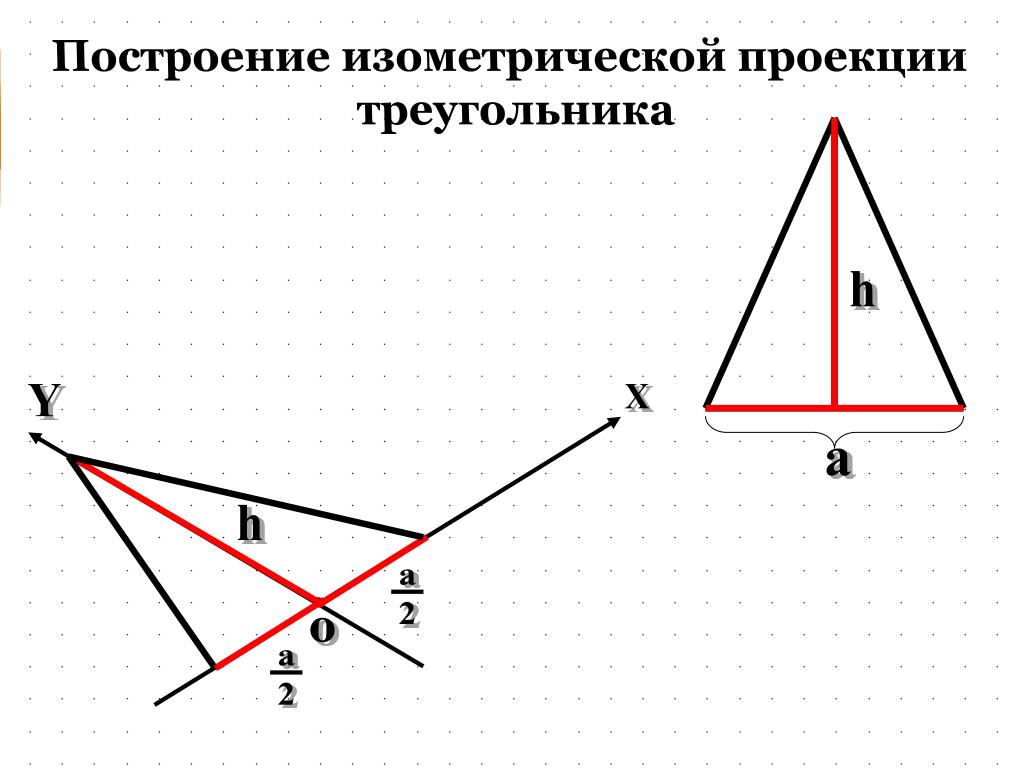
Изометрическая проекция треугольника

При создании 3D-изометрических объектов, содержащих треугольники, не забывайте учитывать закон перспективы для более натурального отображения объектов в пространстве.

Построение изометрической проекциии треугольника