Грани треугольной пирамиды: как их правильно исследовать и понять
Треугольная пирамида — это увлекательная геометрическая фигура, и для того чтобы лучше понять её структуру, необходимо подробно изучить её грани. В этой подборке вы найдете полезные советы, которые помогут вам разобраться в ключевых особенностях граней треугольной пирамиды и научат правильно работать с такими фигурами в различных задачах.

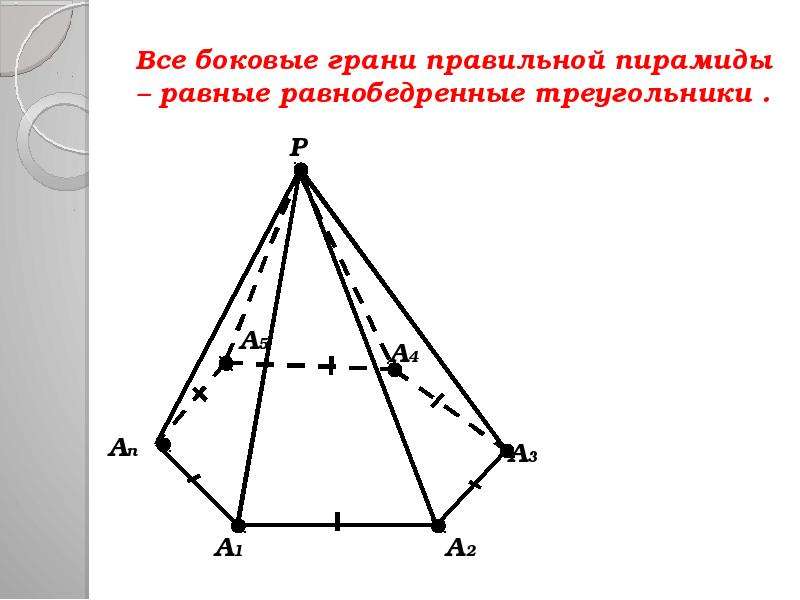
Для начала стоит определить, что треугольная пирамида имеет три боковые грани и одну основание, которое является равнобедренным треугольником.

Лекция 4. Многогранники. Часть 4.
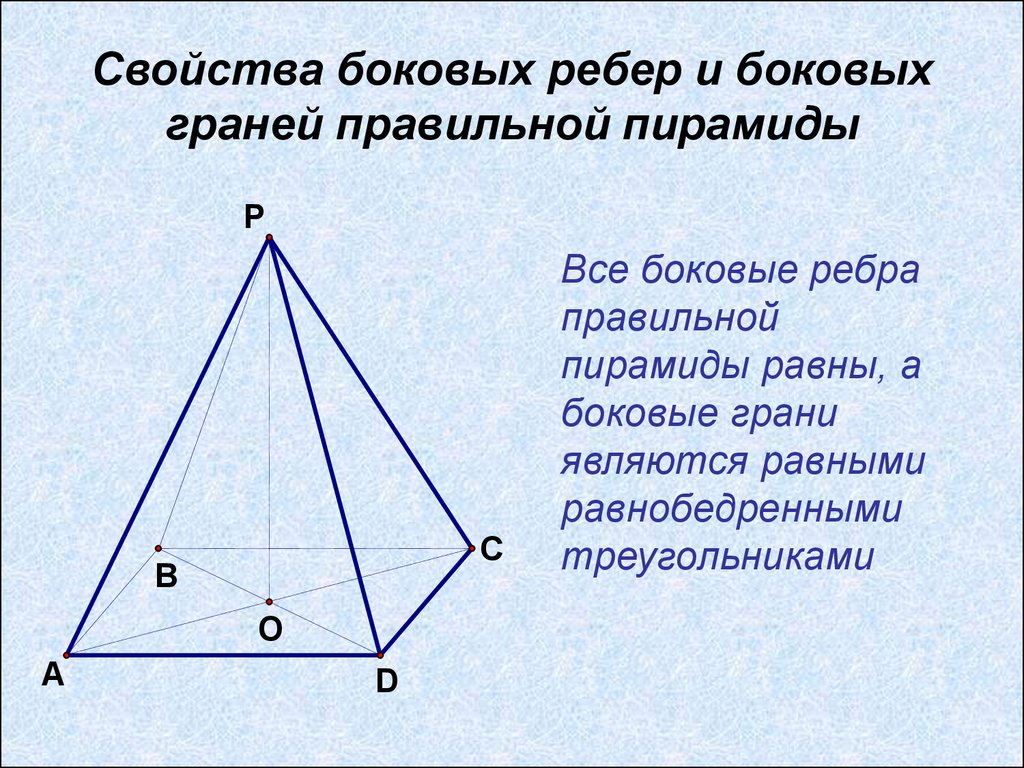
Понимание свойств каждой грани треугольной пирамиды помогает точно рассчитать её площадь и объём, что важно для многих задач.

За халявой переходи в шапку профиля #огэ #онлайншкола #математика #егэ
Грани треугольной пирамиды всегда являются треугольниками, и их площадь можно вычислить по стандартным формулам для площади треугольника.

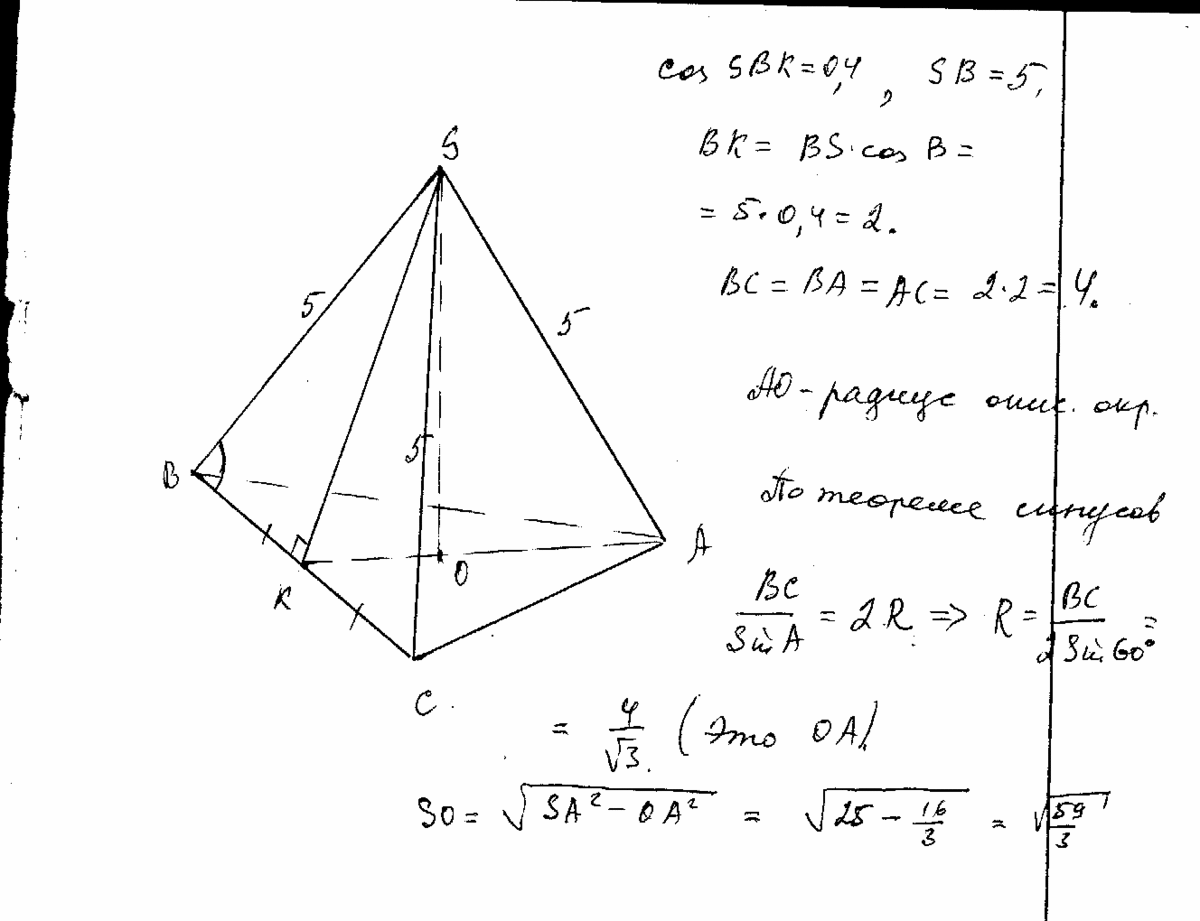
№258. Боковое ребро правильной четырехугольной пирамиды образует угол в 60° с плоскостью основания.

Важно помнить, что все боковые грани пирамиды одинаковы, что даёт определённые симметричные свойства фигуры.
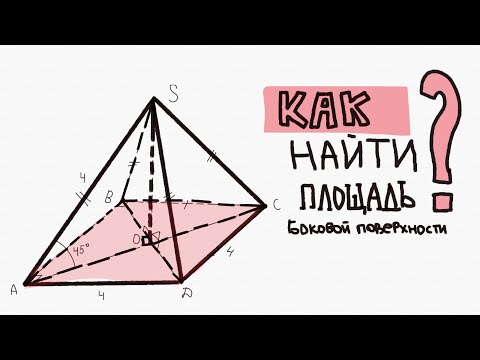
КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?
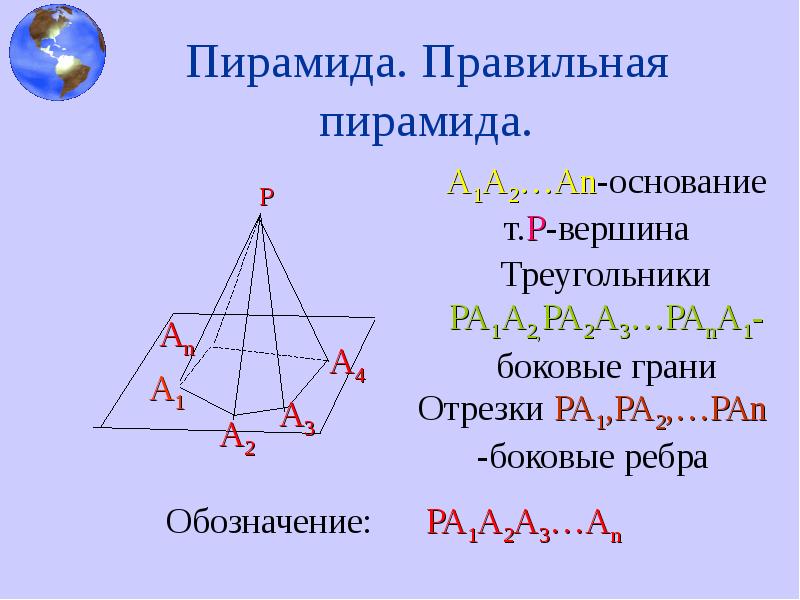
Если треугольная пирамида правильная, то её высота будет перпендикулярна к основанию, а все боковые грани будут равнобедренными треугольниками.

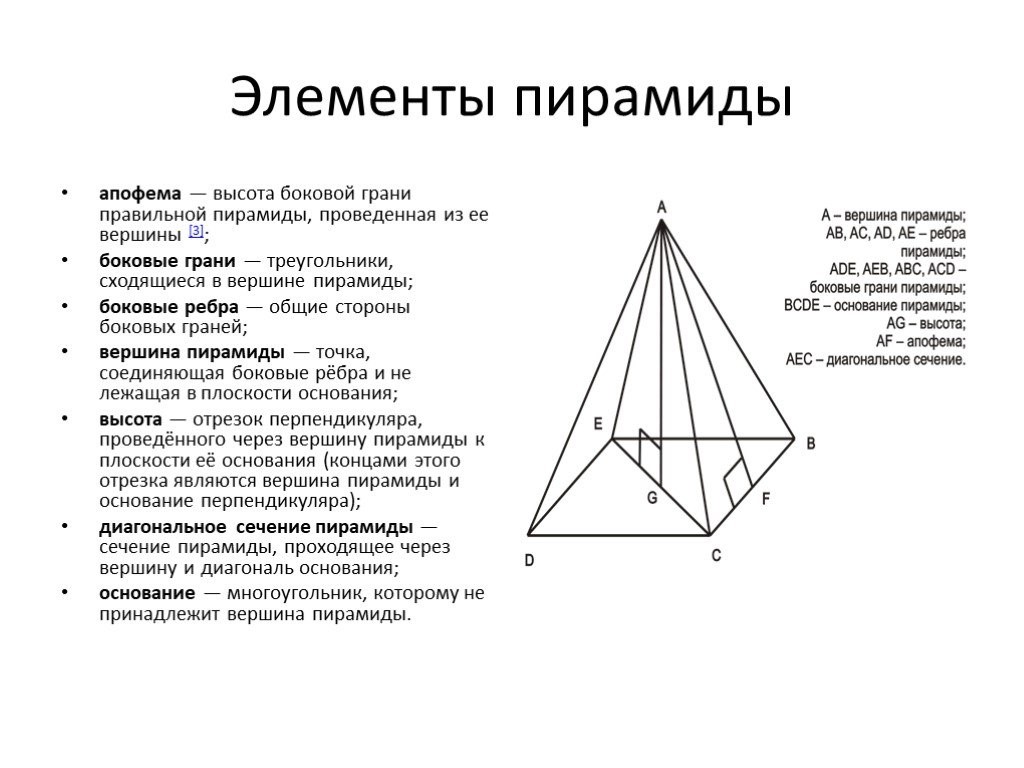
Правильная треугольная пирамида.
Для нахождения объёма треугольной пирамиды используйте формулу V = (1/3) * S_основание * h, где S_основание — площадь основания, а h — высота пирамиды.
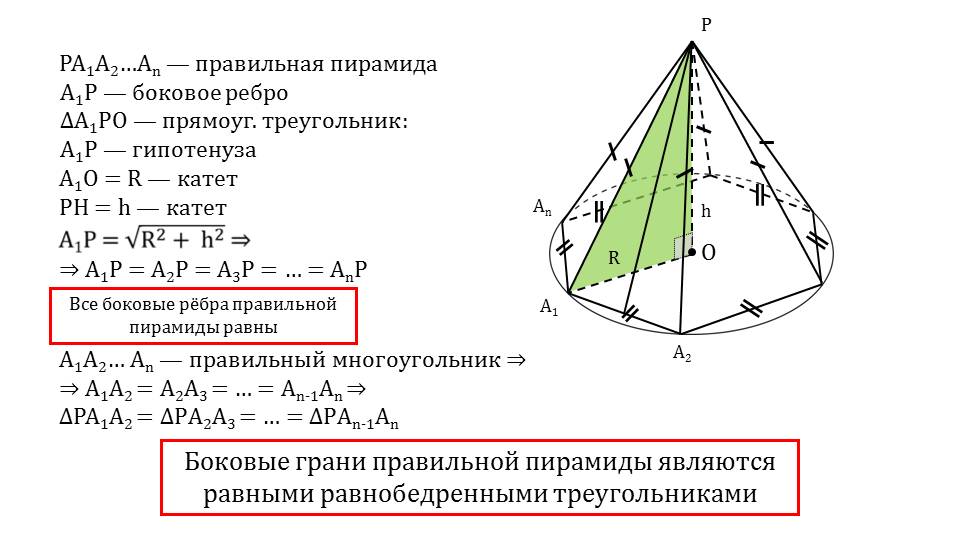
Для более точного анализа каждой грани пирамиды полезно изучить её проекции на различные плоскости, что помогает понять её структуру.
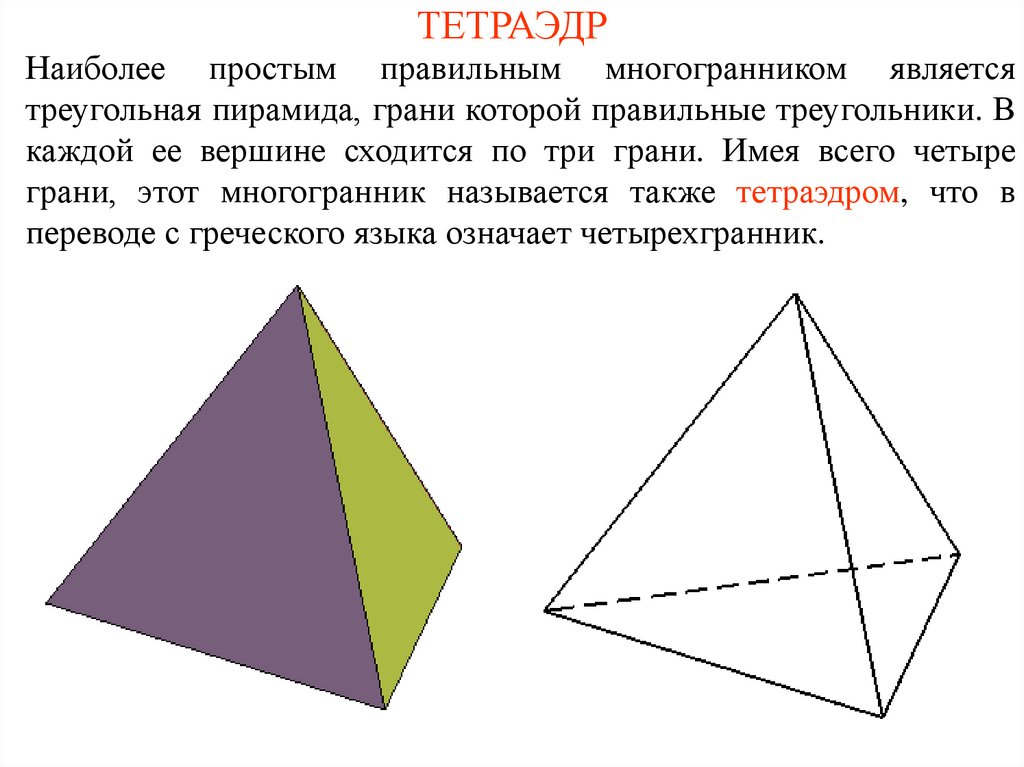
При решении задач с треугольной пирамидой учитывайте, что важными параметрами являются как стороны граней, так и углы между ними.

Как строить сечения тетраэдра и пирамиды
Используйте треугольные пирамиды в качестве примеров для изучения свойств симметрии и многогранников, что расширяет ваше понимание геометрии.
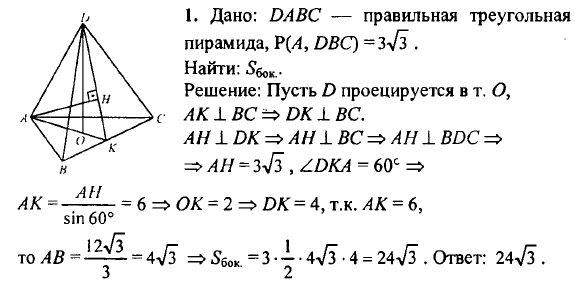
Если вам нужно найти площадь боковой поверхности пирамиды, просто сложите площади всех её боковых граней, используя стандартные геометрические формулы.
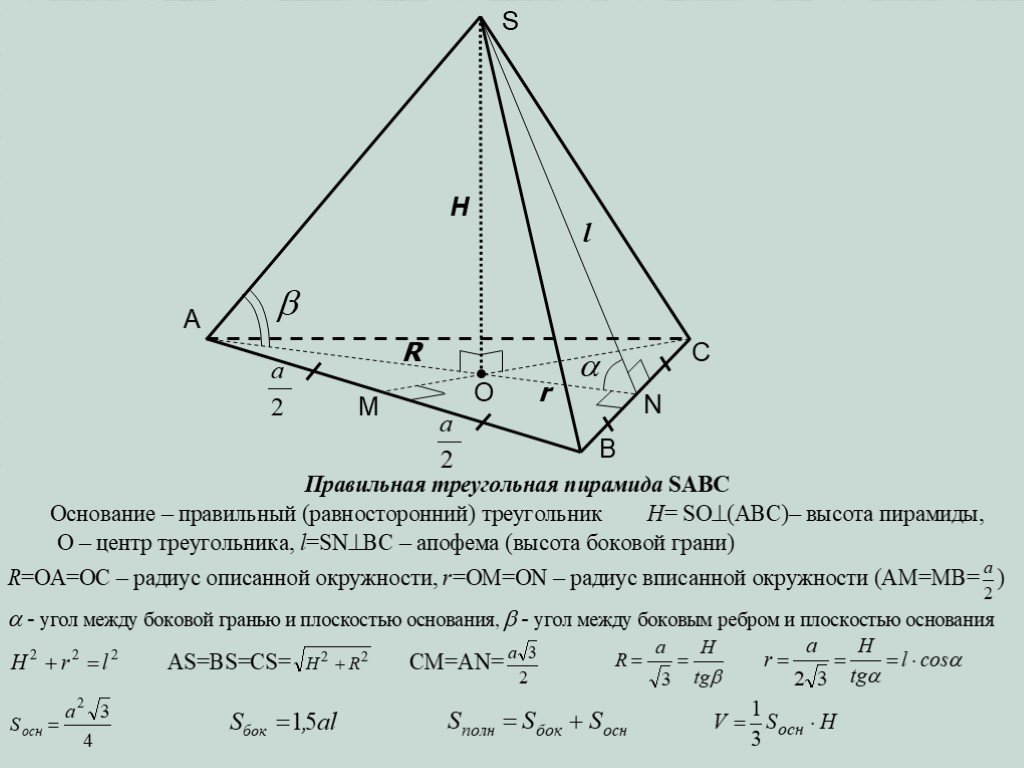

ПРОСТОЙ СПОСОБ КАК СОБРАТЬ ПИРАМИДКУ РУБИКА(МЕФФЕРТА)