Площадь поверхности куба: формулы и полезные советы для 5 класса
На этой странице вы найдете подробное объяснение того, как вычислить площадь поверхности куба для учеников 5 класса. Мы рассмотрим основные формулы, шаги решения задач, а также дадим полезные советы для лучшего усвоения материала.


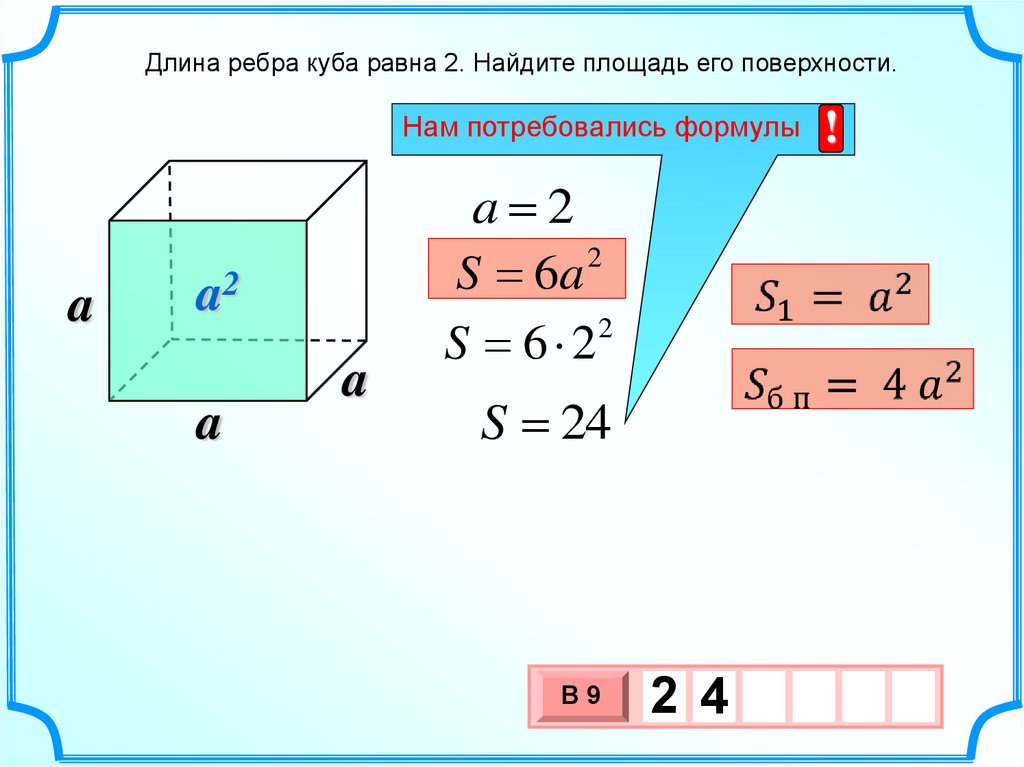
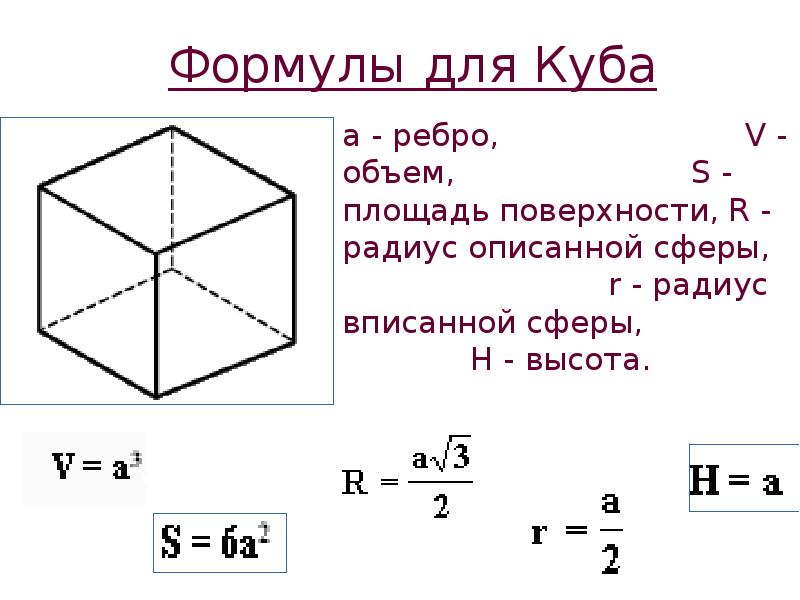
Запомните, что куб — это фигура с шестью равными квадратными гранями. Для вычисления площади поверхности достаточно найти площадь одной грани и умножить ее на 6.

КАК НАЙТИ ПЛОЩАДЬ ПОВЕРХНОСТИ КУБА, ЕСЛИ ИЗВЕСТНО РЕБРО? Примеры - МАТЕМАТИКА 5 класс
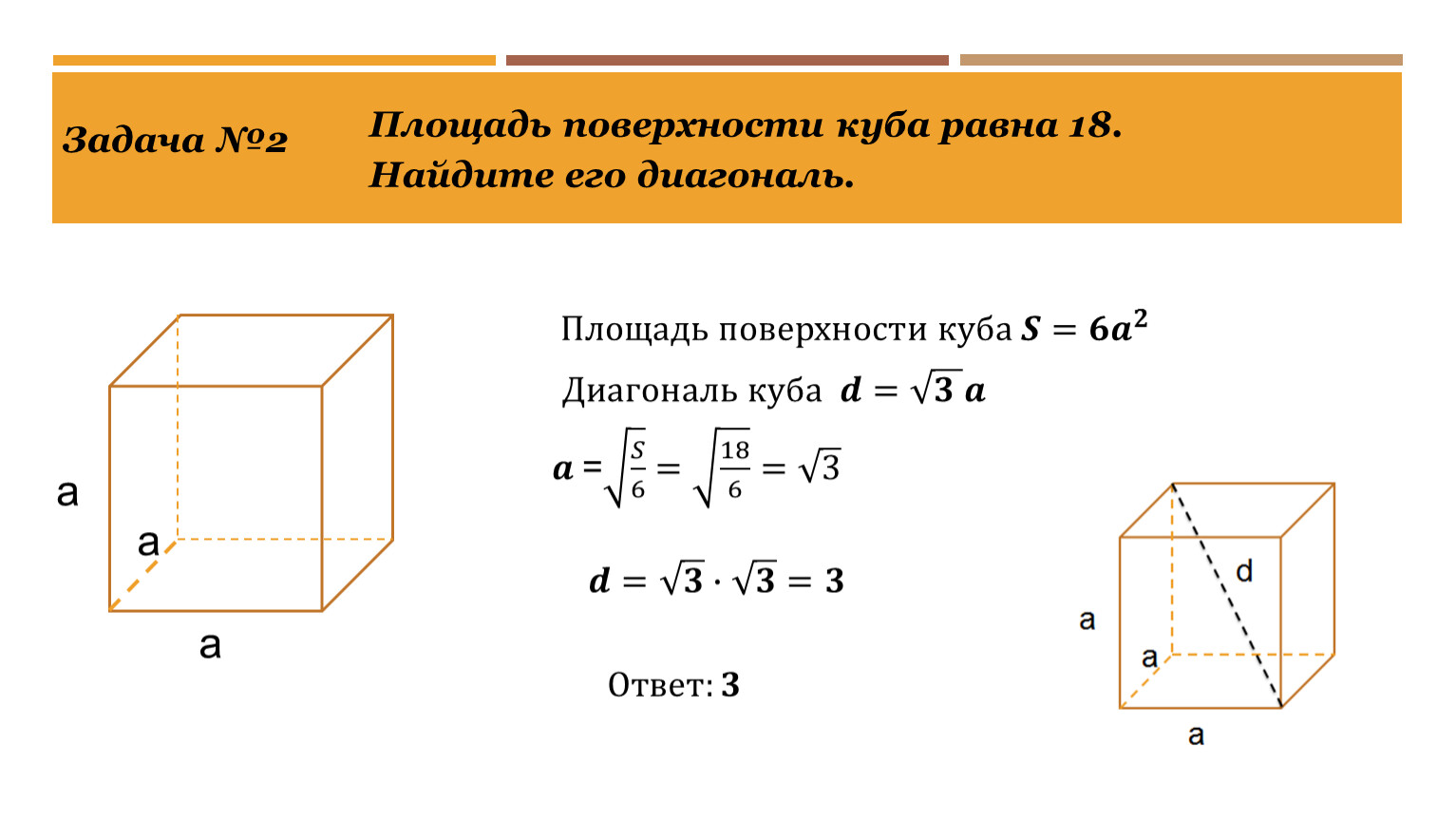
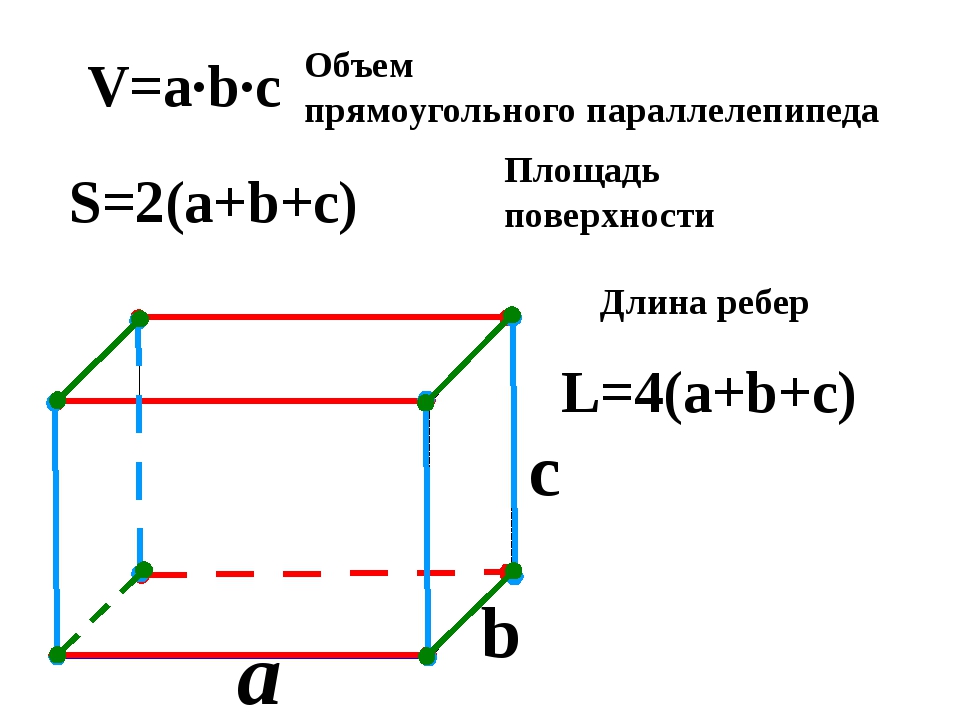
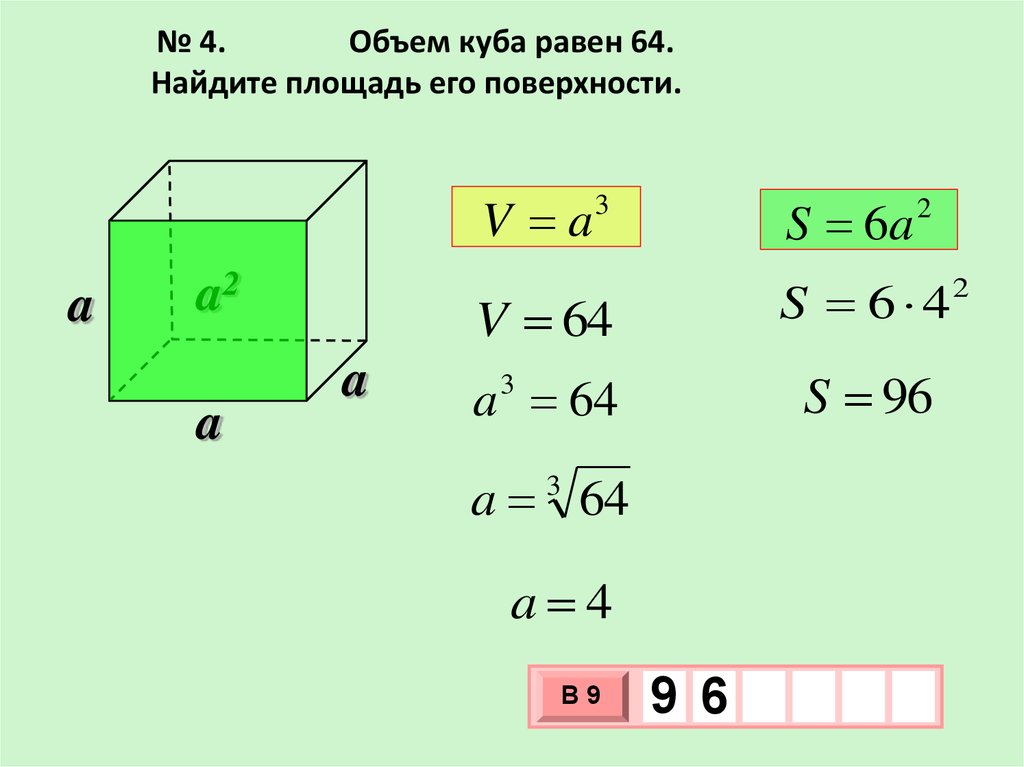
Площадь одной грани куба можно найти, возведя длину ребра в квадрат: S = a², где а — длина ребра куба.

Математика 5 класс. Объем куба Соотношения между единицами объема
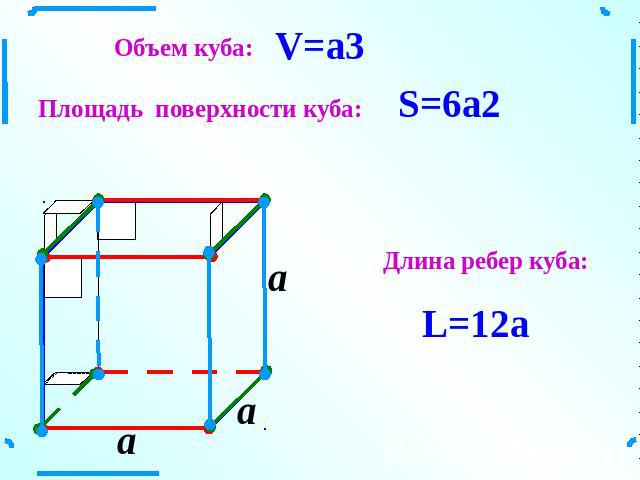
Если вам дана длина ребра, например 5 см, то площадь одной грани будет равна 5² = 25 см².

Площадь квадрата. Как найти площадь квадрата?

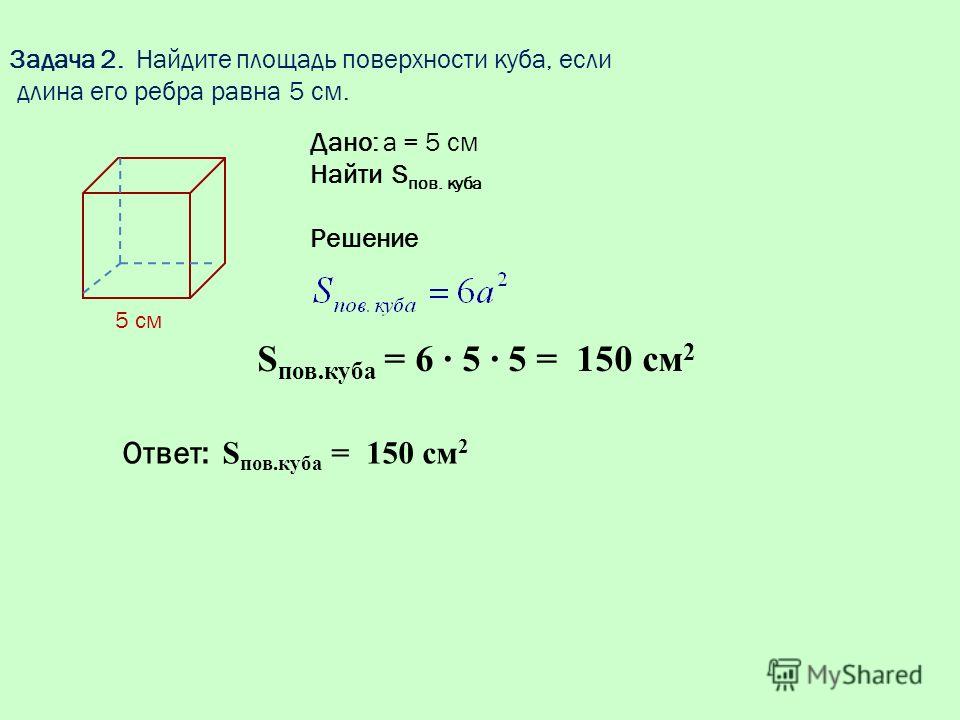
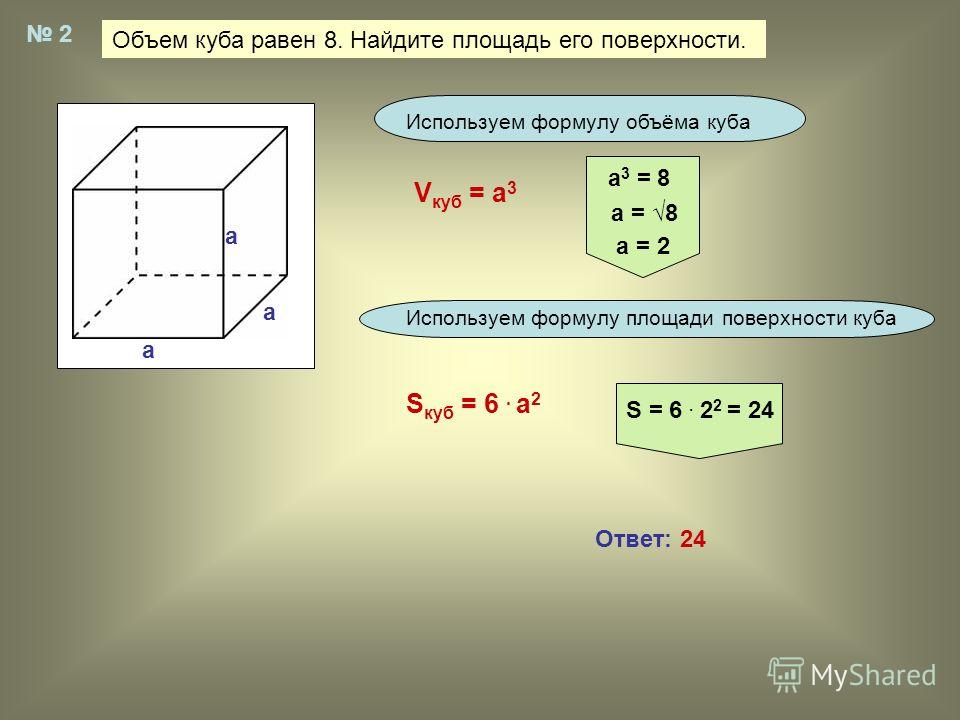
Не забывайте, что куб имеет 6 граней, и площадь поверхности будет равна 6 умножить на площадь одной грани. То есть, для куба с ребром 5 см площадь поверхности составит 6 * 25 = 150 см².

Математика 5 класс. Объем Объем прямоугольного параллелепипеда

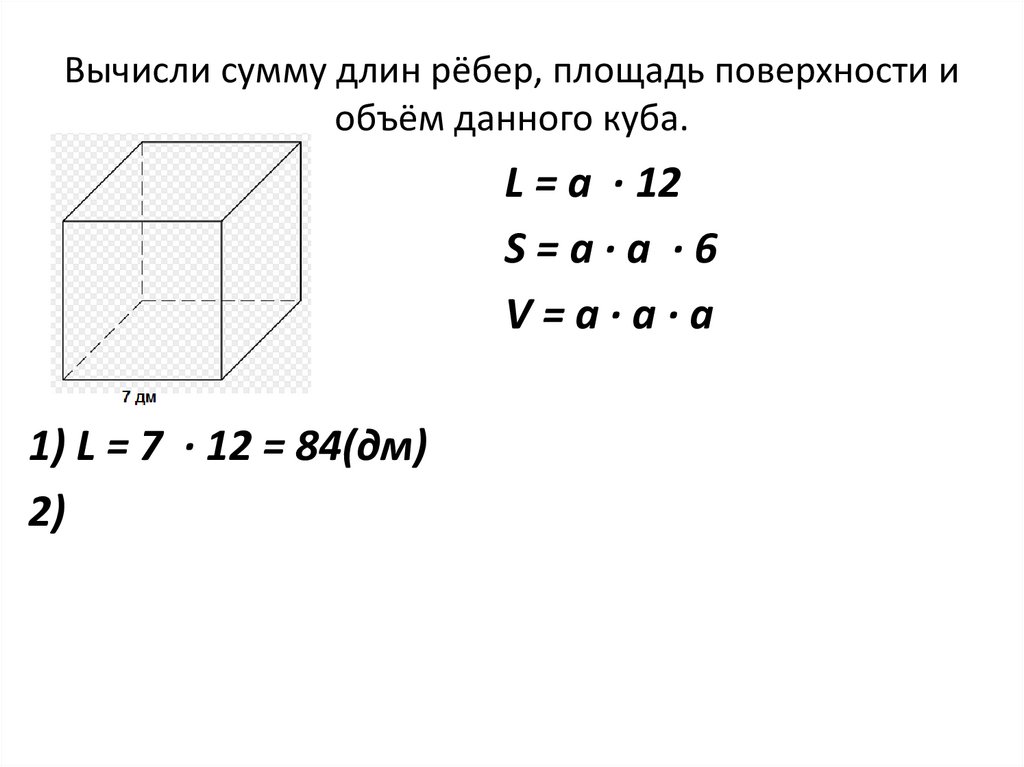
Для выполнения задач на нахождение площади поверхности куба важно точно измерить длину его ребра, так как от этого зависит весь расчет.

5 класс, 21 урок, Объемы. Объем прямоугольного параллелепипеда
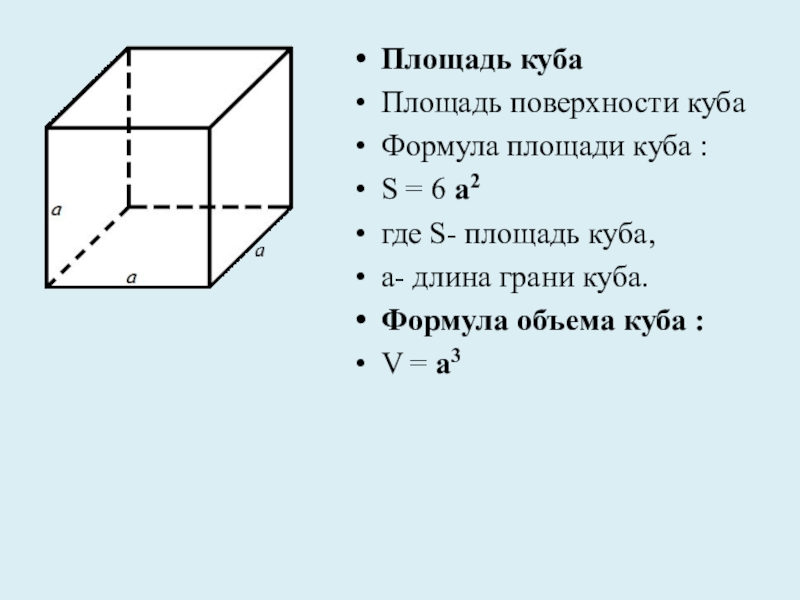
Если ребро куба задано в другом измерении (например, в метрах), не забудьте перевести все данные в одну систему единиц (например, в сантиметры), чтобы не допустить ошибок в расчетах.

КАК НАЙТИ ОБЪЕМ КУБА ПО РЕБРУ? Примеры - МАТЕМАТИКА 5 класс
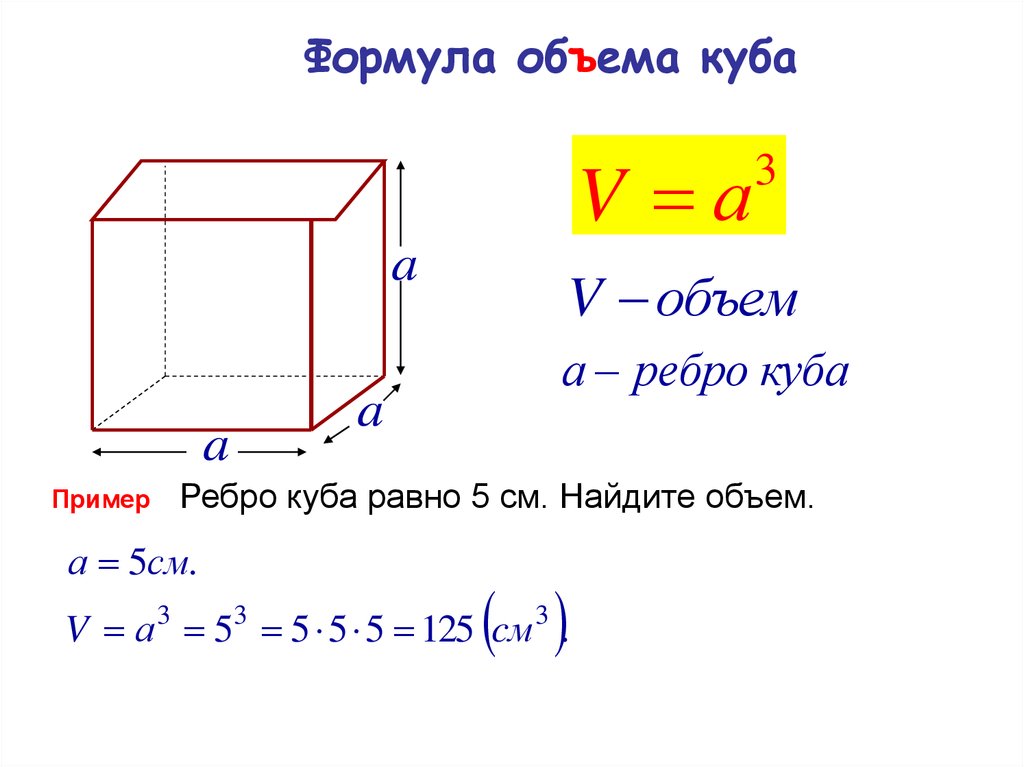

Проверьте свой расчет: площадь одной грани куба должна быть положительным числом, а итоговая площадь поверхности — также положительной.
Используйте формулу площади поверхности куба только для правильных кубов, где все ребра одинаковы по длине.

Формулы. Вычисление по формулам. 5 класс.
Чтобы лучше понять тему, попробуйте решить несколько задач на вычисление площади поверхности куба с разной длиной ребра.

21. Площадь. Формула площади прямоугольника - 5 класс
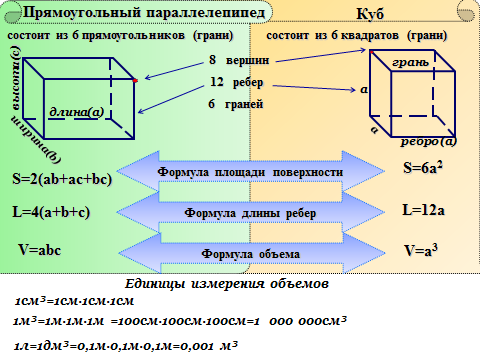
Не забывайте, что куб — это частный случай параллелепипеда, где все рёбра одинаковы. Поэтому формулы для расчета площади поверхности куба просты и легко запоминаются.
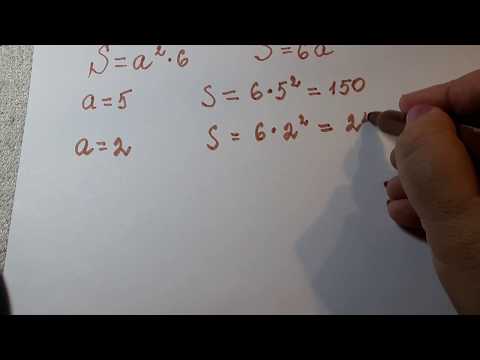
Площадь поверхности куба. 5 likerkacinema.ru(базовый уровень)