Как правильно решить неполное квадратное уравнение: пошаговое руководство и полезные советы
Неполные квадратные уравнения встречаются в математике довольно часто. В этой статье мы рассмотрим, как правильно решать такие уравнения, используя различные методы и приемы. Подробные шаги, примеры и советы помогут вам легко справиться с задачами любого уровня сложности.
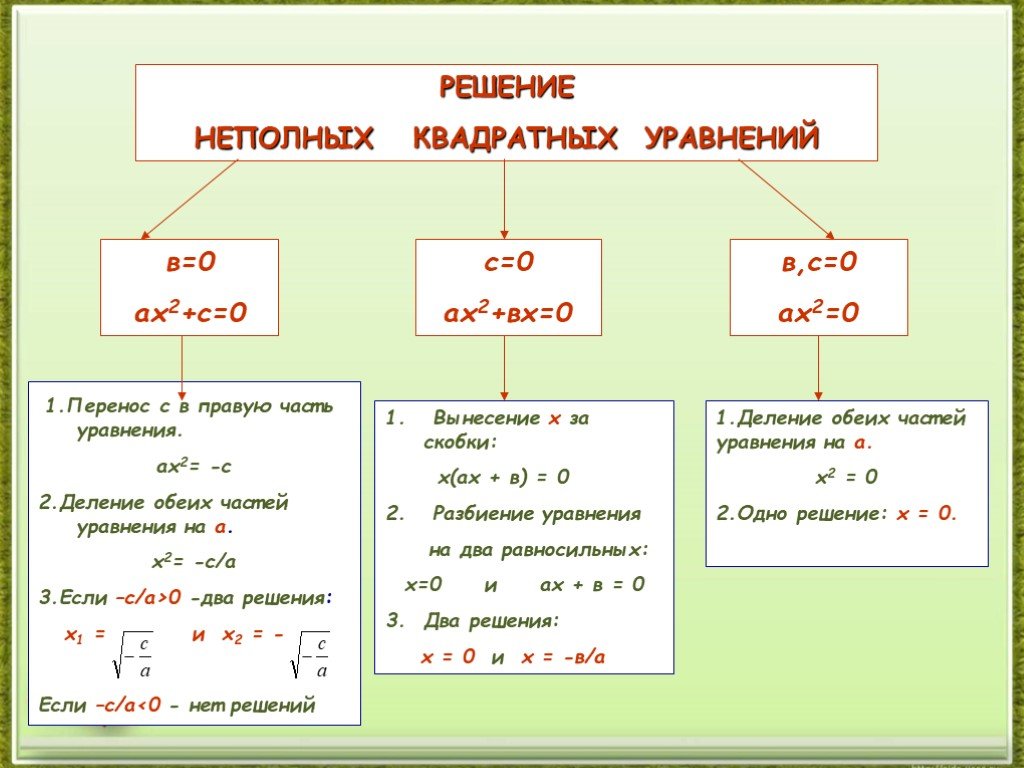

При решении неполного квадратного уравнения всегда внимательно проверяйте, какой коэффициент отсутствует (при a, b или c). Это поможет выбрать правильный метод.

Школьник из Тамбова, набравший 300 баллов на ЕГЭ, рассказал о подготовке к экзаменам

Не забывайте о дискриминанте. В случае неполного уравнения, если один из коэффициентов равен нулю, дискриминант можно вычислить по упрощенной формуле.

Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполные


Если в уравнении отсутствует линейный член (b = 0), то решение можно получить через извлечение квадратного корня из свободного члена.

АЛГЕБРА 8 класс : Решение неполных квадратных уравнений - Видеоурок


Если отсутствует свободный член (c = 0), то уравнение можно решить путем вынесения общего множителя и получения корней через разделение на коэффициент при x².

МАТЕМАТИКА 8 класс - Неполные Квадратные Уравнения. Как решать Неполные Квадратные Уравнения?
Используйте метод подбора, если коэффициенты простые и легко поддаются нахождению корней.

Квадратные уравнения. Решение неполных квадратных уравнений.


В случае отсутствия линейного члена и свободного члена (b = 0, c = 0) уравнение примет вид ax² = 0, и его решение будет очевидным.
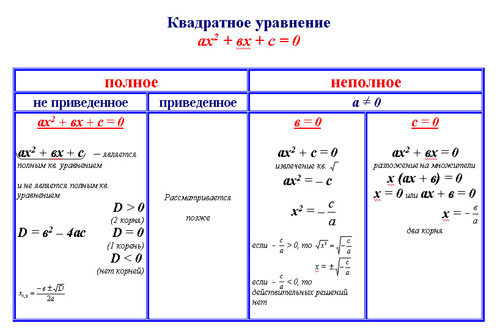

Не забывайте, что для уравнений вида ax² + c = 0 (где b = 0), решение можно получить через извлечение корня из отрицательной константы.
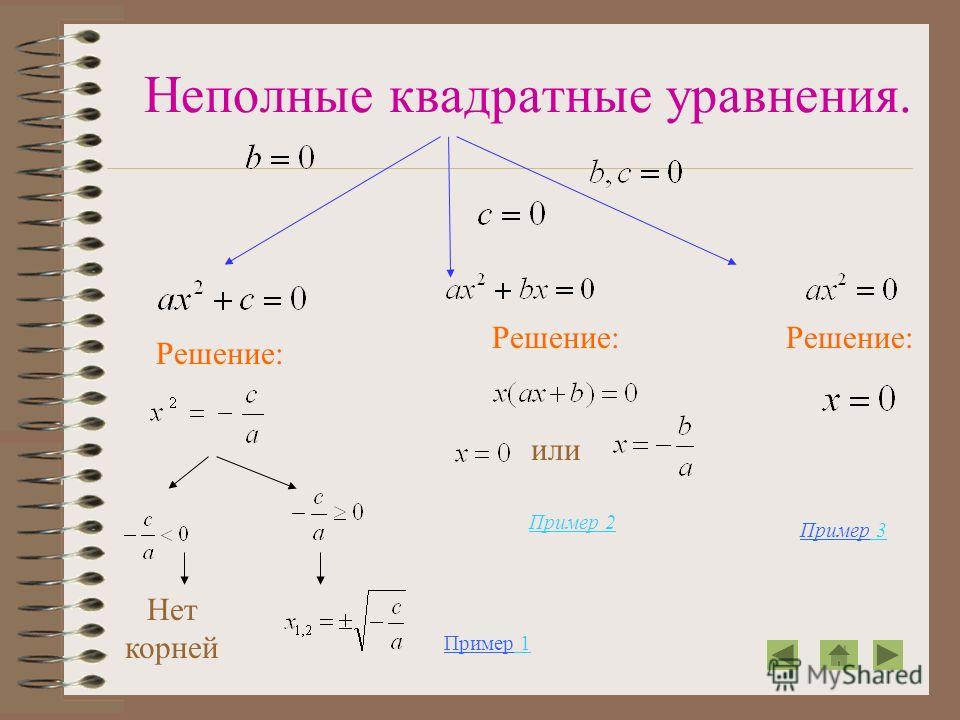
Всегда перепроверяйте свои корни, подставляя их в исходное уравнение. Иногда можно получить ошибочные результаты из-за неверной трактовки знаков.

Использование графического метода может быть полезным для визуализации решения неполных квадратных уравнений.

Решение неполных квадратных уравнений всегда должно учитывать возможные особенности, например, случай, когда решение — единственный корень или два одинаковых корня.