Парабола на графике функции: как читать и анализировать ее форму и особенности
На этой странице мы разберем основные аспекты работы с параболой на графике функции, объяснив, как правильно читать формулы и определять ключевые моменты, такие как вершина, ось симметрии и другие важные параметры графика. Эта информация поможет вам легче решать задачи и анализировать поведение квадратичной функции.
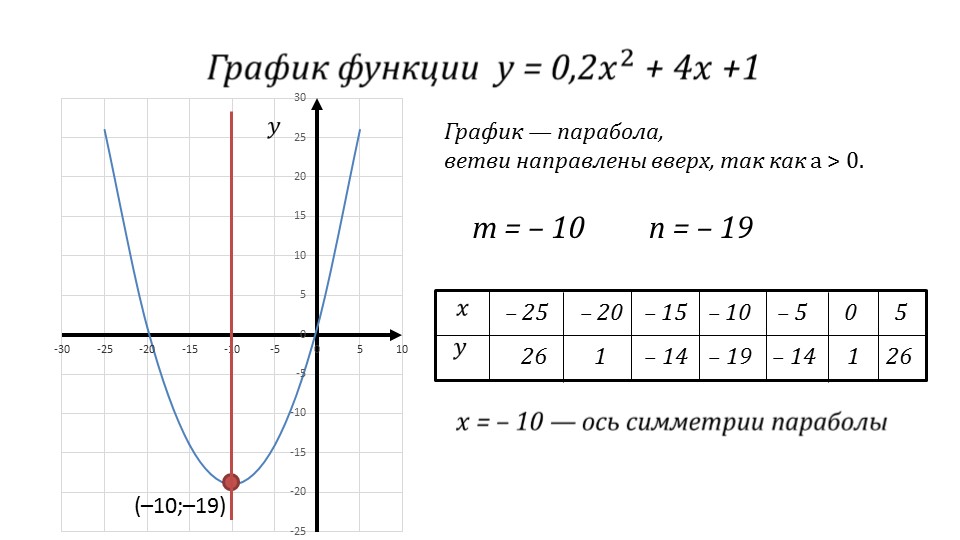
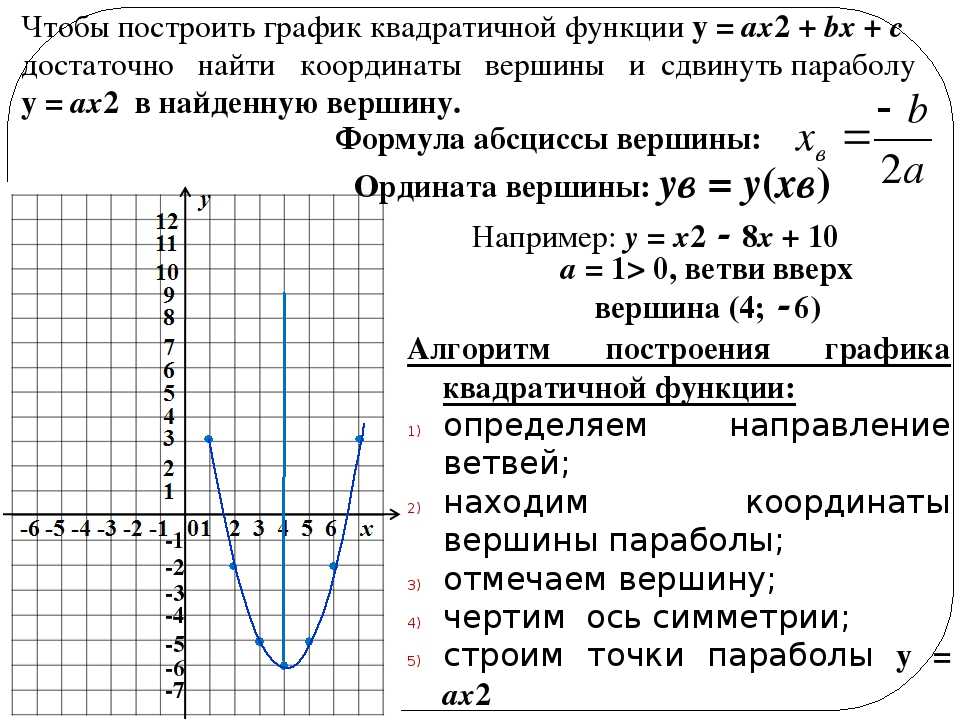
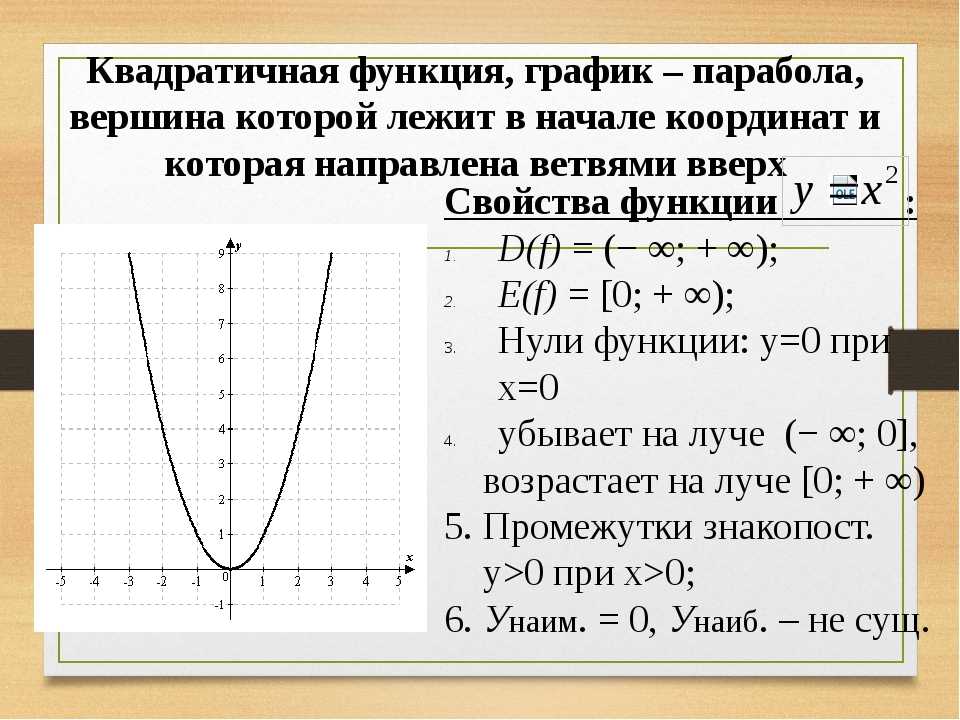
Чтобы правильно построить параболу на графике, важно правильно определить коэффициенты уравнения, такие как a, b и c, которые определяют форму и положение параболы.

ОБЪЯСНЕНИЕ ГРАФИКА ПАРАБОЛЫ 😉 ЧАСТЬ I #shorts #егэ #огэ #математика #проценты
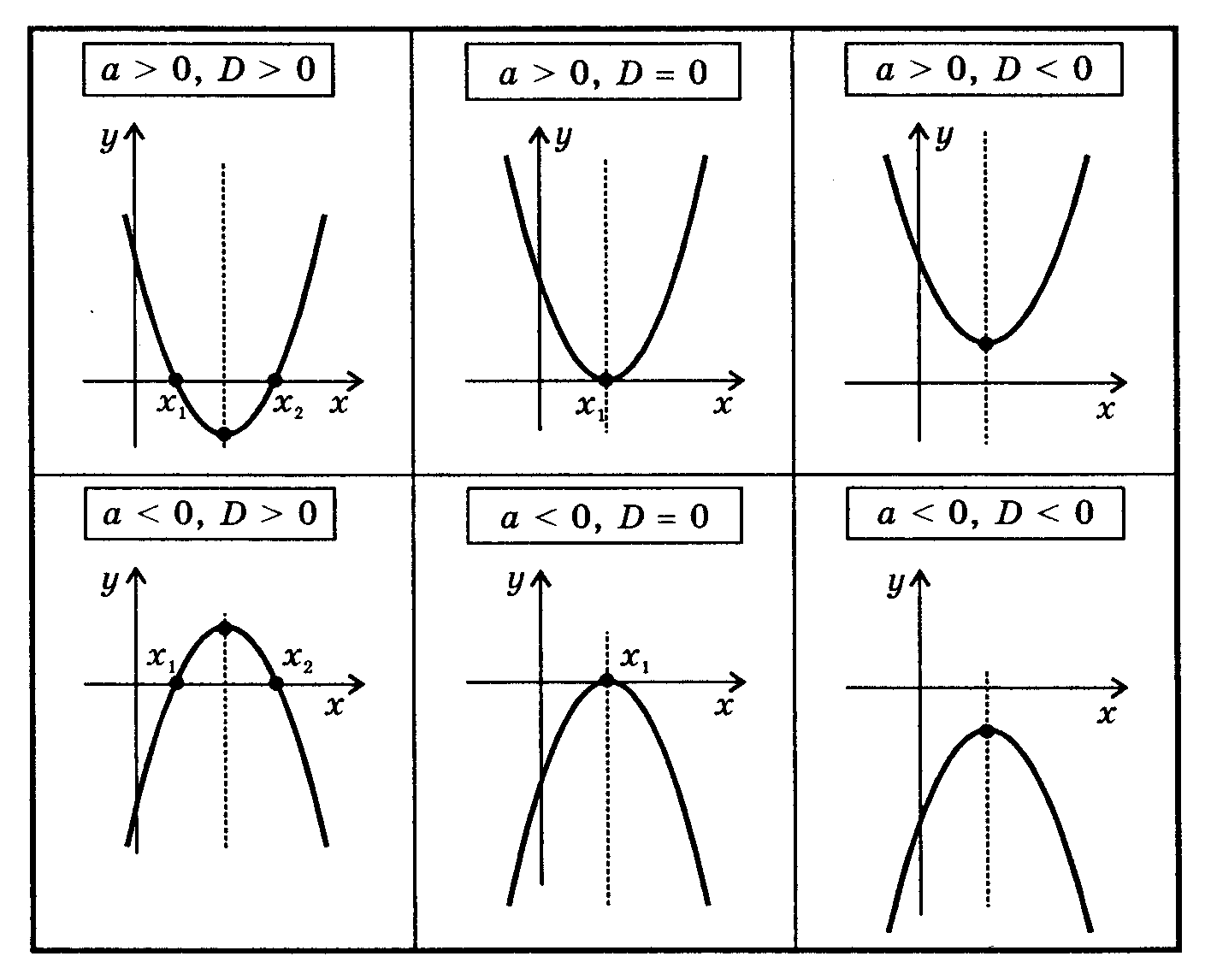
Обратите внимание на знак коэффициента a: если он положительный, парабола открывается вверх, если отрицательный — вниз.

Построение параболы
Вершина параболы является ключевой точкой, и ее координаты можно найти с помощью формулы: x = -b/(2a) и y = f(x).
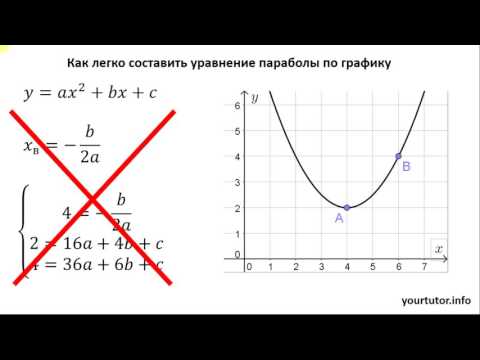
Как легко составить уравнение параболы из графика
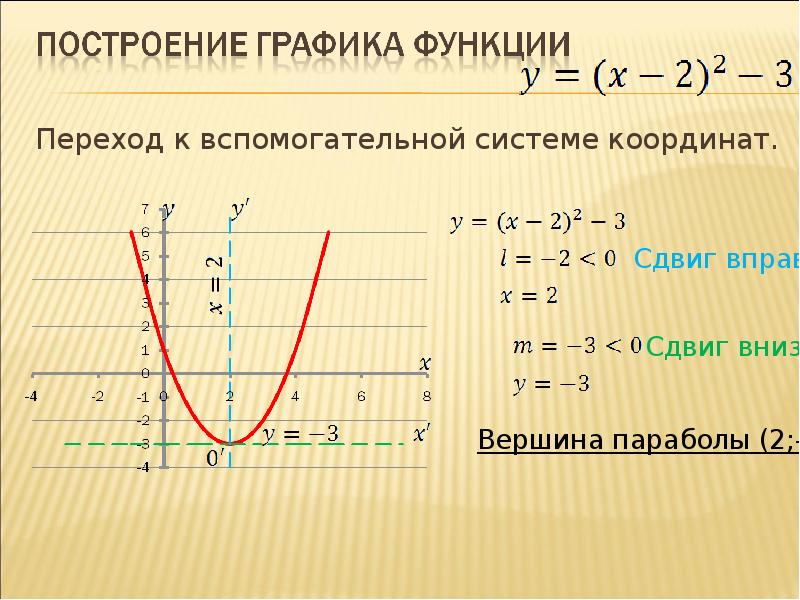
Ось симметрии параболы всегда проходит через ее вершину, и ее уравнение можно записать как x = -b/(2a).

Всё о квадратичной функции. Парабола - Математика TutorOnline


Для того, чтобы точнее изобразить параболу, лучше всего определить хотя бы несколько дополнительных точек на графике, подставив значения x в уравнение.
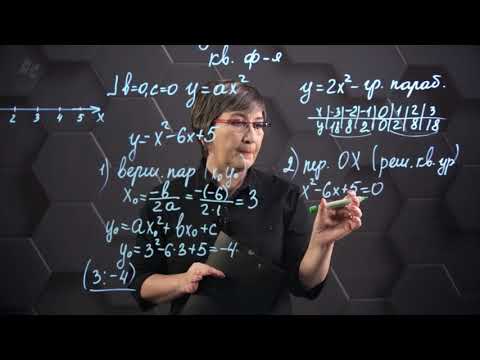
Квадратичная функция и ее график. 8 класс.

Если уравнение функции имеет вид y = ax^2 + bx + c, то его график всегда будет параболой, и важно правильно вычислять все параметры, чтобы понять, как он будет выглядеть.
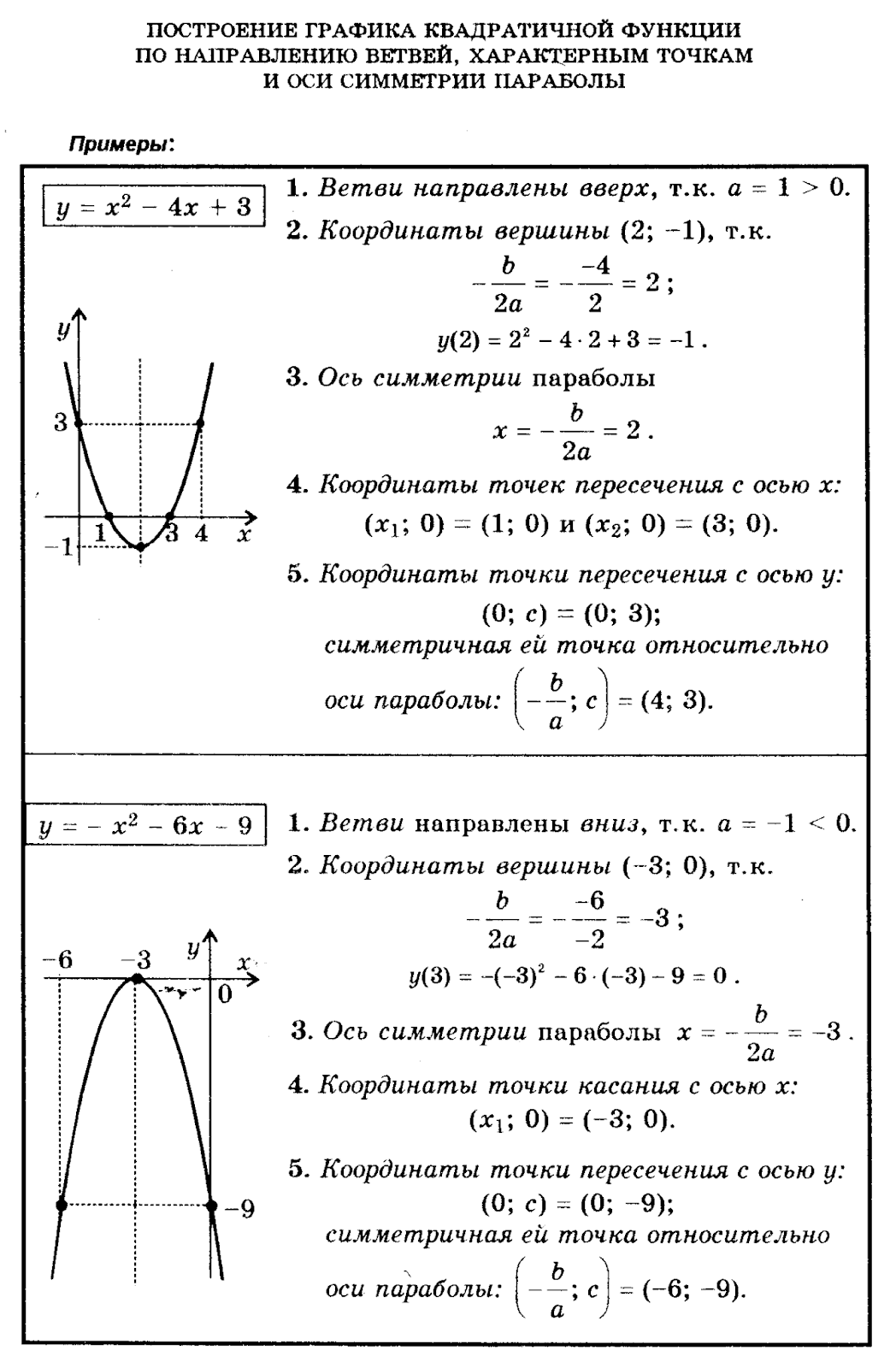
Для более точного анализа графика можно вычислить корни функции с помощью дискриминанта, что поможет понять, пересекает ли парабола ось x и в какой точке.
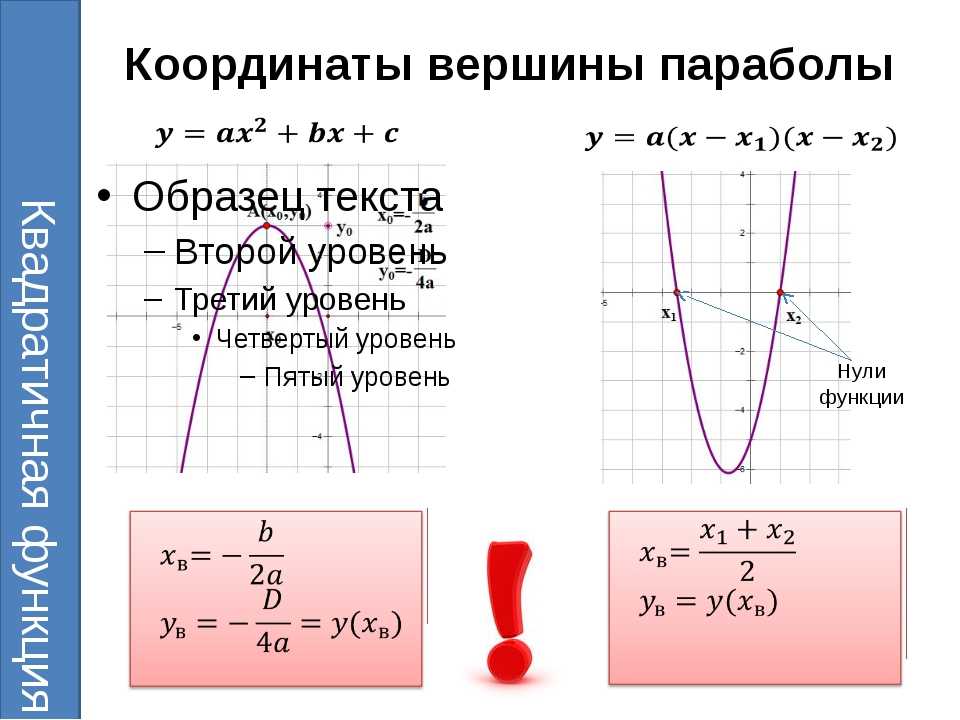
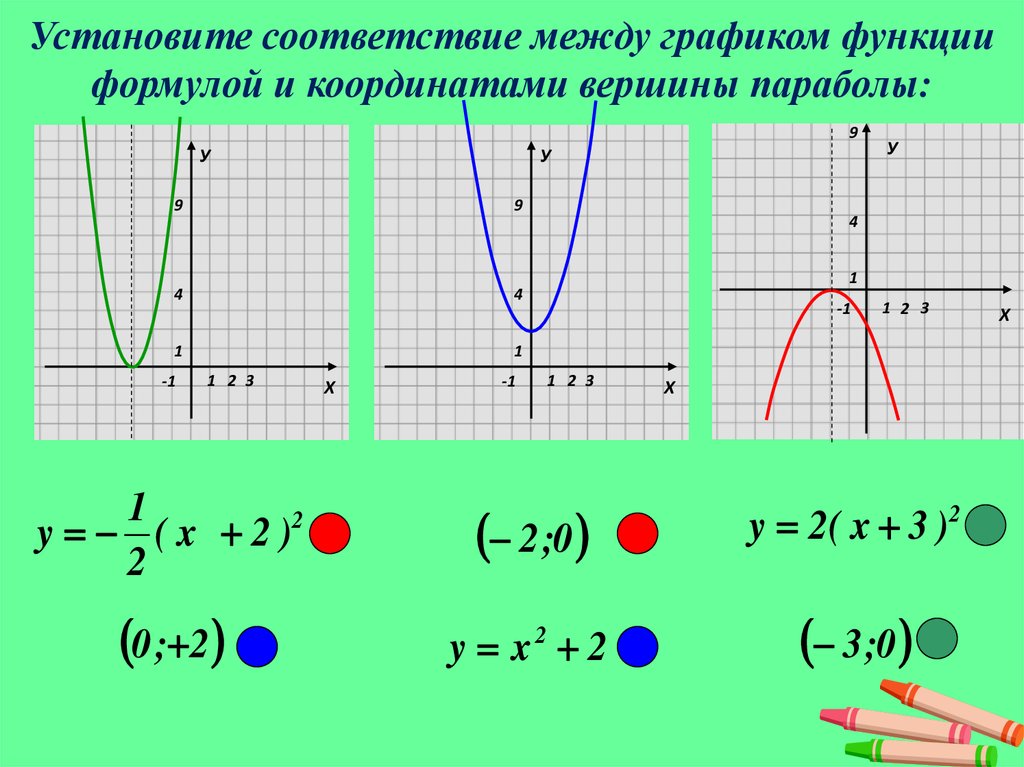
Если дискриминант отрицателен, то парабола не пересекает ось x, и у функции нет действительных корней.

ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график Парабола
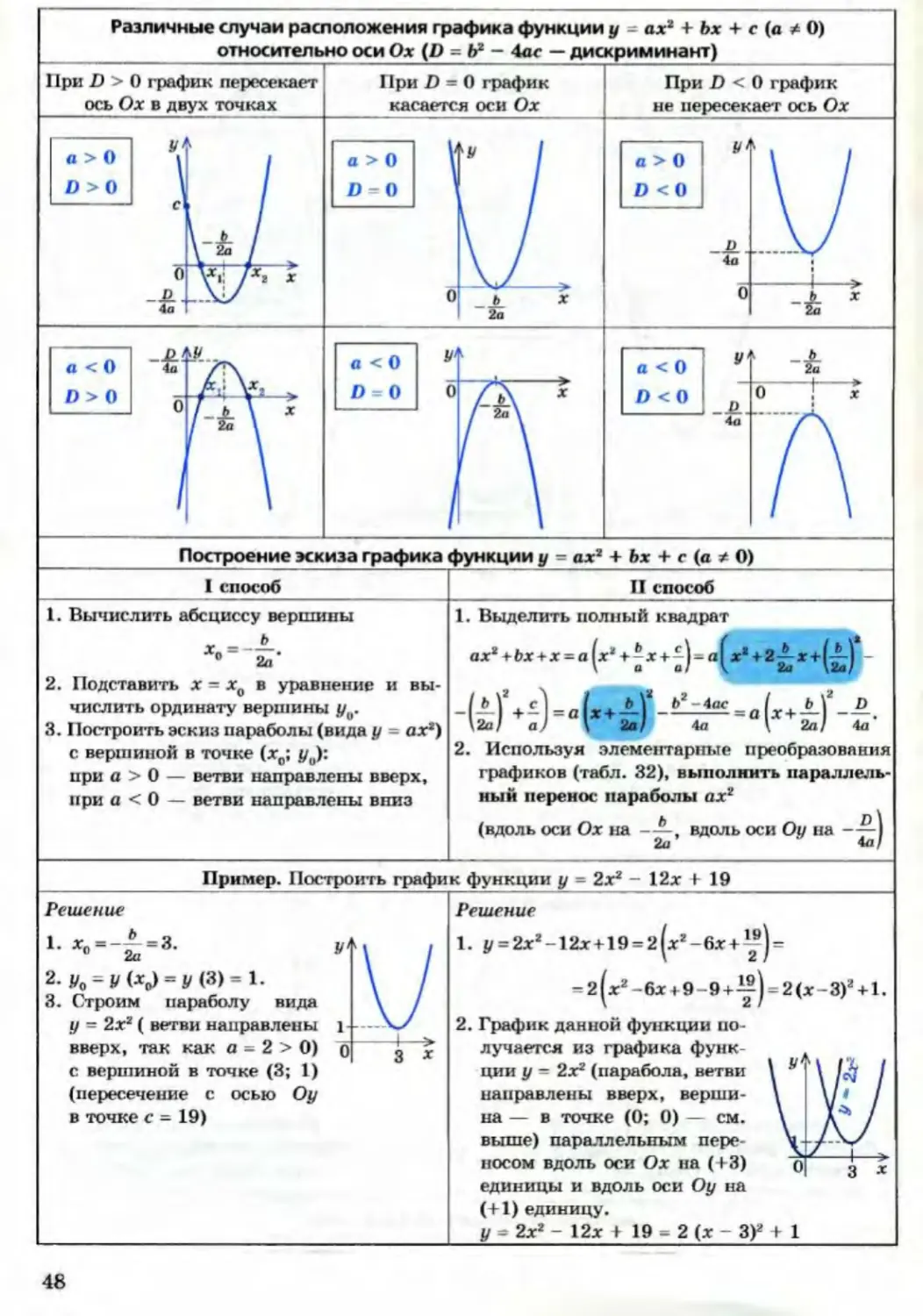
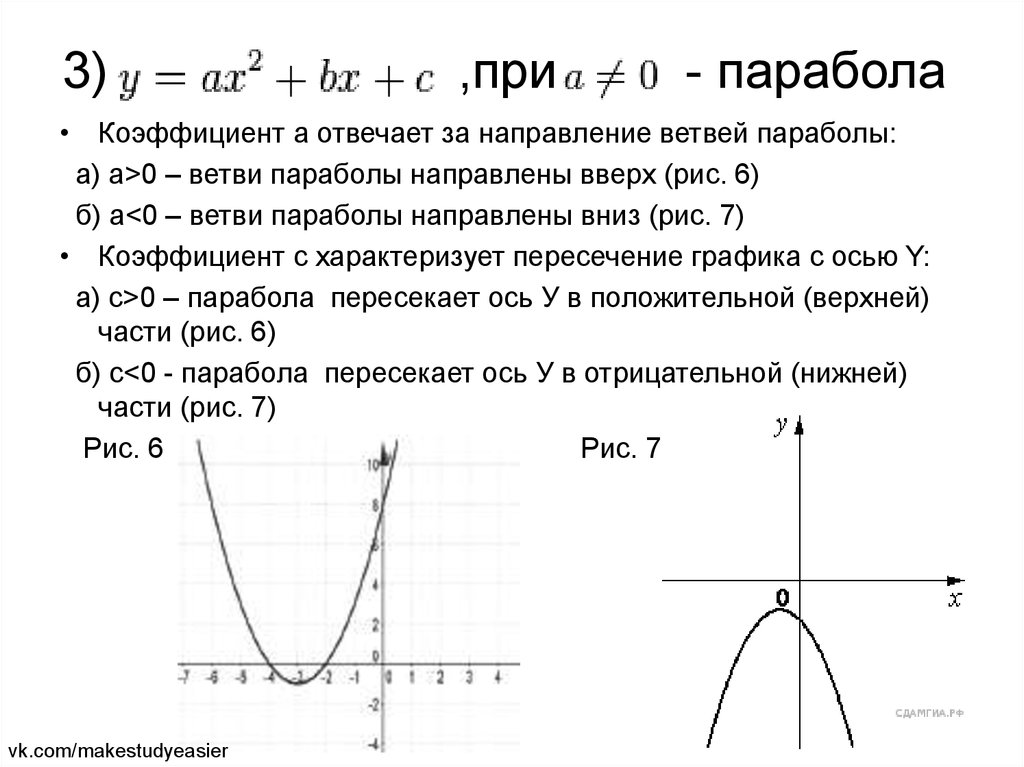
Когда дискриминант положительный, парабола имеет два действительных корня, которые можно найти с помощью формулы x1,2 = (-b ± √D) / (2a).
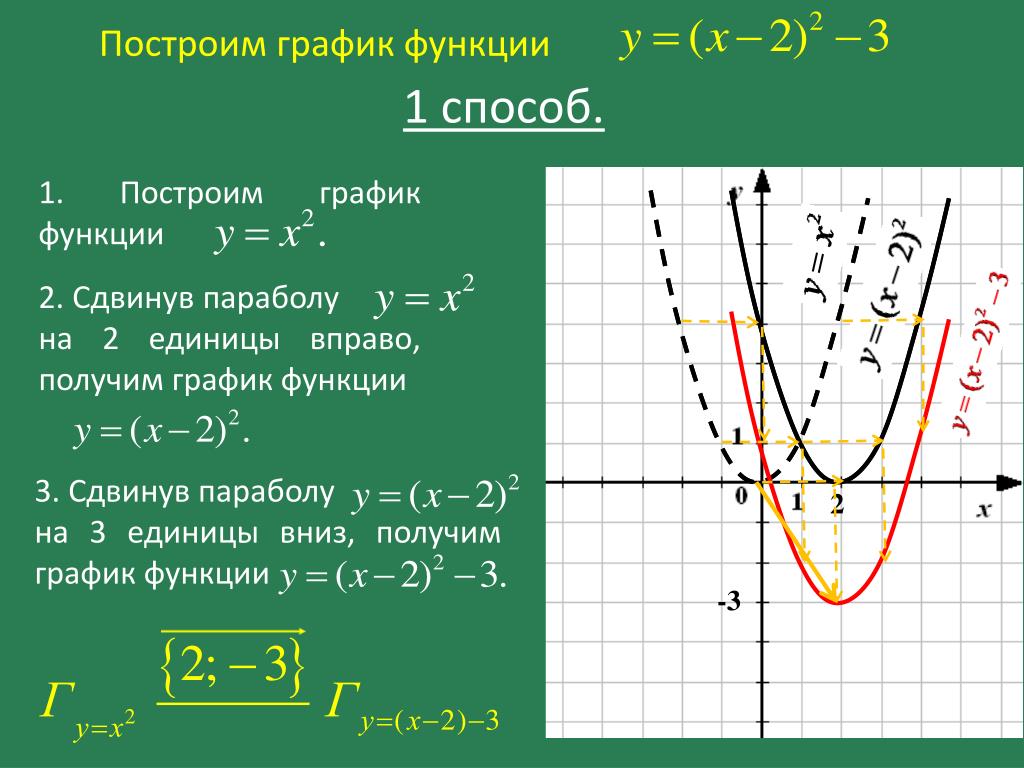
Для лучшего понимания графика, экспериментируйте с изменением коэффициентов a, b и c, чтобы увидеть, как они влияют на форму параболы.
Функция y=x2 и её график – 8 класс алгебра


Квадратичная функция за 5 минут