Как изучать фигуру, возникающую при вращении параболы вокруг оси: ключевые моменты
Фигура, образующаяся при вращении параболы вокруг оси, является интересным объектом в геометрии. Это уникальная форма с множеством практических приложений, например, в архитектуре и физике. Разнообразие таких фигур открывает новые горизонты для инженеров и ученых, исследующих объекты вращения.
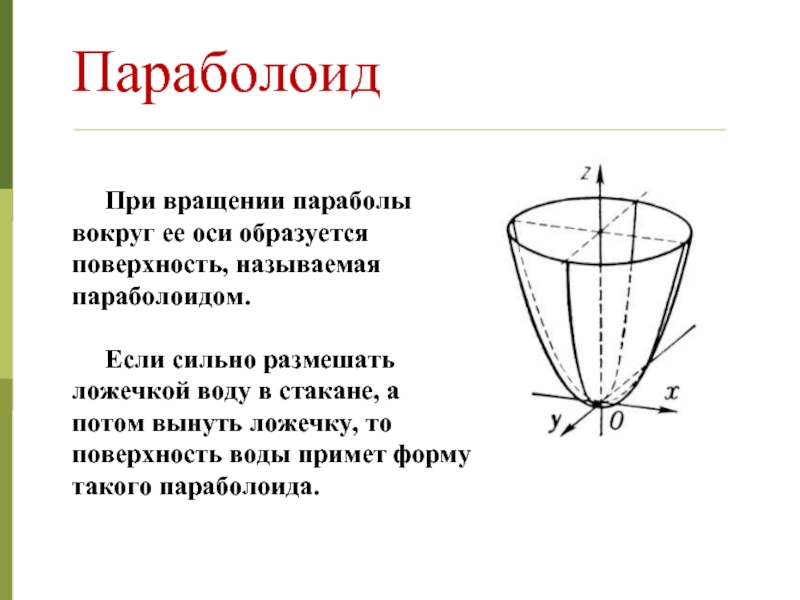

Для правильного представления фигуры начните с анализа исходной параболы, которая будет вращаться.
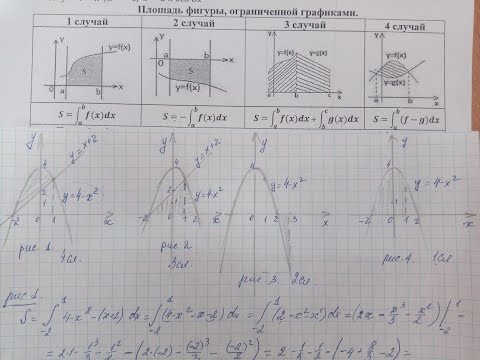
Нахождение площадей фигур, ограниченных графиками

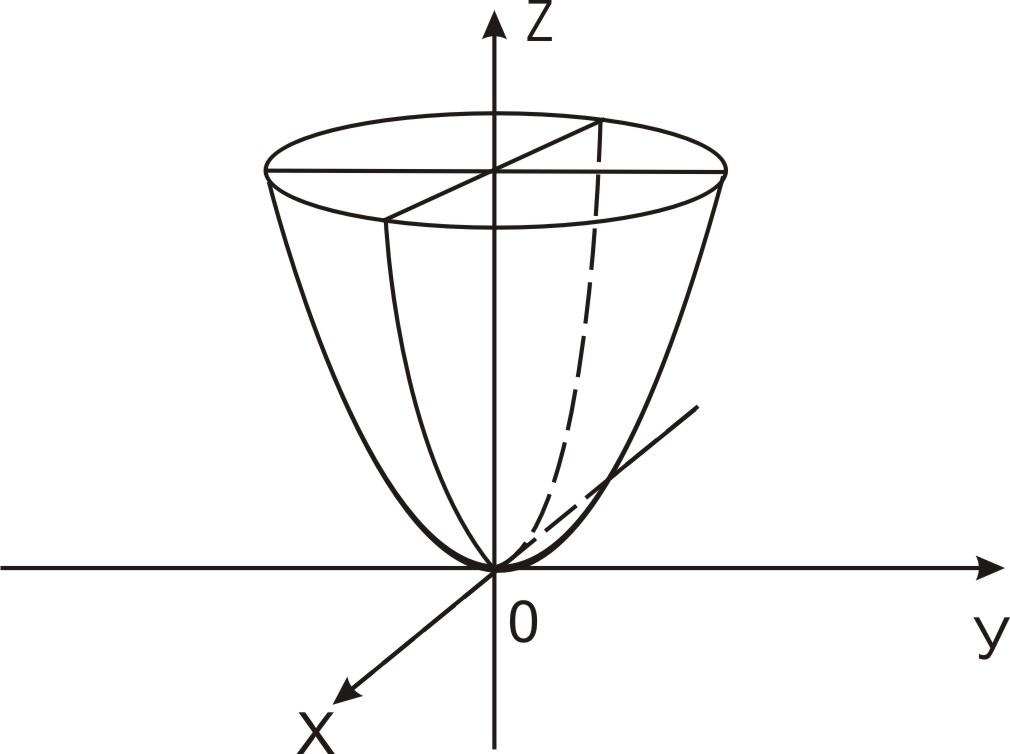
При построении таких фигур важно учитывать ось вращения, так как она определяет конечную форму объекта.

Шарик, катящийся по вращающейся платформе

Используйте компьютерное моделирование, чтобы визуализировать результат вращения параболы и лучше понять ее геометрические свойства.

Объем тела вращения на примере тора. 2 способа


Обратите внимание на симметрию фигуры, которая играет важную роль в ее анализе и применении.

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорение

Для расчета объема и площади поверхности фигуры, полученной при вращении, применяйте соответствующие интегралы.
ПОИ5. Объём тела вращения (вокруг оси ОY).

Исследуйте зависимости между параметрами параболы и характеристиками получаемой фигуры, такими как высота и радиус.

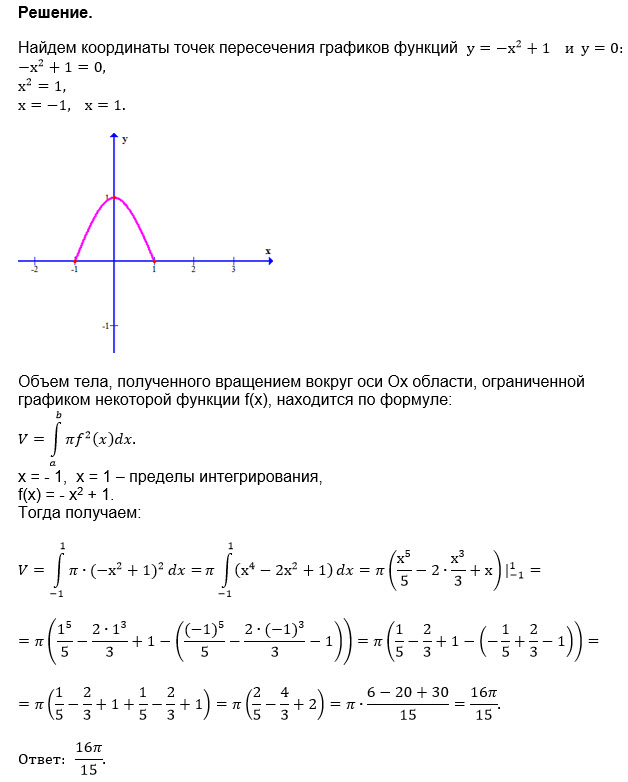
Не забывайте про различные варианты осей вращения — это может сильно изменить форму получаемой фигуры.

Видеоурок \
Практические применения таких фигур можно найти в строительстве, например, в проектировании куполов и зеркал.
Для создания точных моделей используйте специализированное программное обеспечение, которое позволяет моделировать вращение параболы в 3D-пространстве.
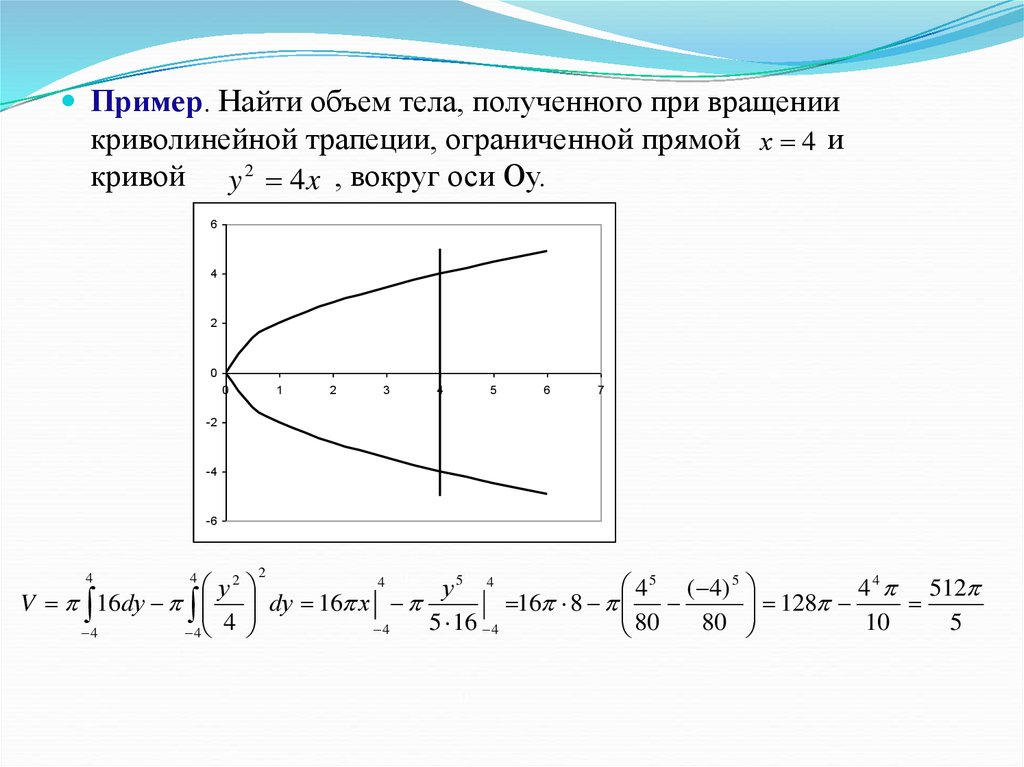
Не забывайте о математической теории, которая лежит в основе формирования таких фигур: это поможет вам глубже понять их свойства.

Skewer Hyperbolic Paraboloid


Интегралы №13 Объем тела вращения