Числовые характеристики непрерывных случайных величин: понятие, виды и их применение

Числовые характеристики непрерывной случайной величины играют ключевую роль в статистическом анализе и теории вероятностей. Эти показатели помогают описать поведение случайной величины, её распределение и закономерности, которые могут быть полезны при решении реальных задач. На странице представлены основные типы таких характеристик, их значения и практическое применение в различных областях науки и техники.

Для более точного анализа случайной величины всегда стоит учитывать её математическое ожидание, которое является важным ориентиром для дальнейших вычислений.

Если вам нужно оценить степень изменчивости случайной величины, то стоит обратить внимание на её дисперсию и стандартное отклонение.

В случае работы с нормальным распределением, важно помнить, что его числовые характеристики часто имеют симметричное распределение относительно математического ожидания.

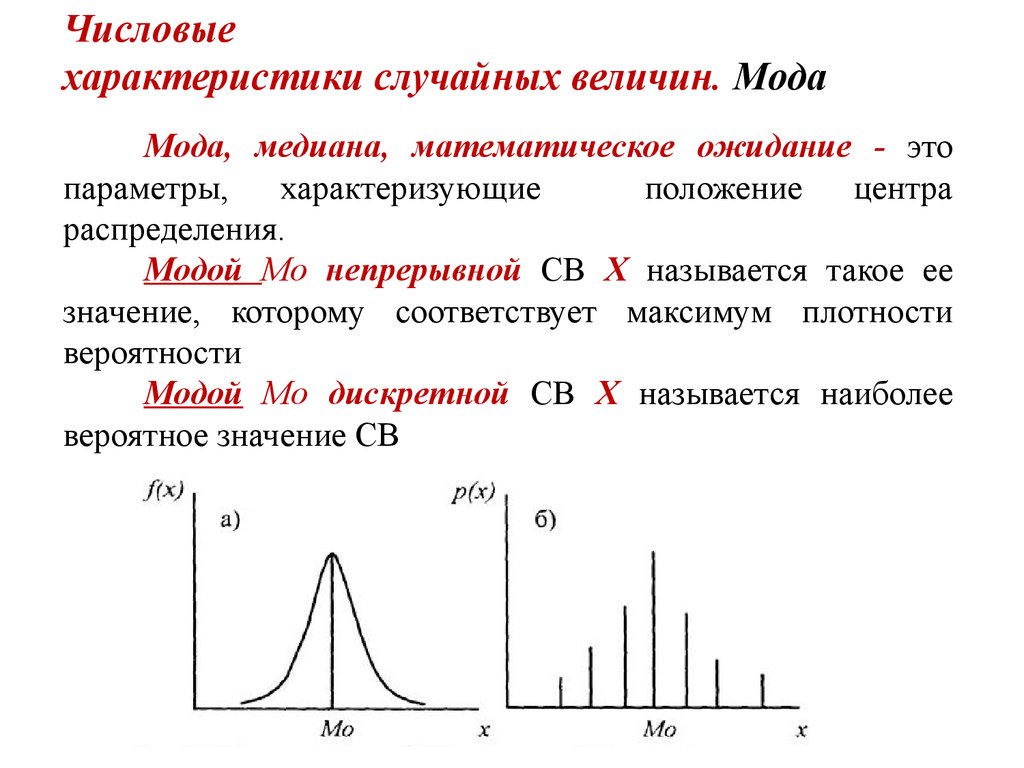
Рассматривая распределение случайной величины, стоит использовать такие характеристики, как медиана и мода, для анализа центральных тенденций.

Если распределение случайной величины асимметрично, то коэффицент асимметрии может стать полезным инструментом для более точного описания данных.

При оценке распределения важно учитывать показатели эксцесса, которые могут дать представление о толщине хвостов распределения.

Не забывайте о кумулятивной функции распределения, которая помогает визуализировать и понимать вероятность попадания случайной величины в тот или иной интервал.

Важно учитывать, что числовые характеристики случайной величины могут изменяться при изменении её распределения или условий эксперимента.

Для анализа различных случайных величин и их зависимостей часто используют корреляцию и ковариацию, которые помогают выявить взаимосвязь между величинами.

При построении моделей с использованием случайных величин всегда проверяйте гипотезы о распределении данных для повышения точности результатов.