Основы анализа асимптот: важность для точности построения графиков функций
Асимптоты играют ключевую роль при анализе поведения функции на бесконечности или вблизи точек, где она может стремиться к бесконечности или не быть определенной. В этом разделе вы найдете полезные советы по их вычислению и визуализации на графиках.

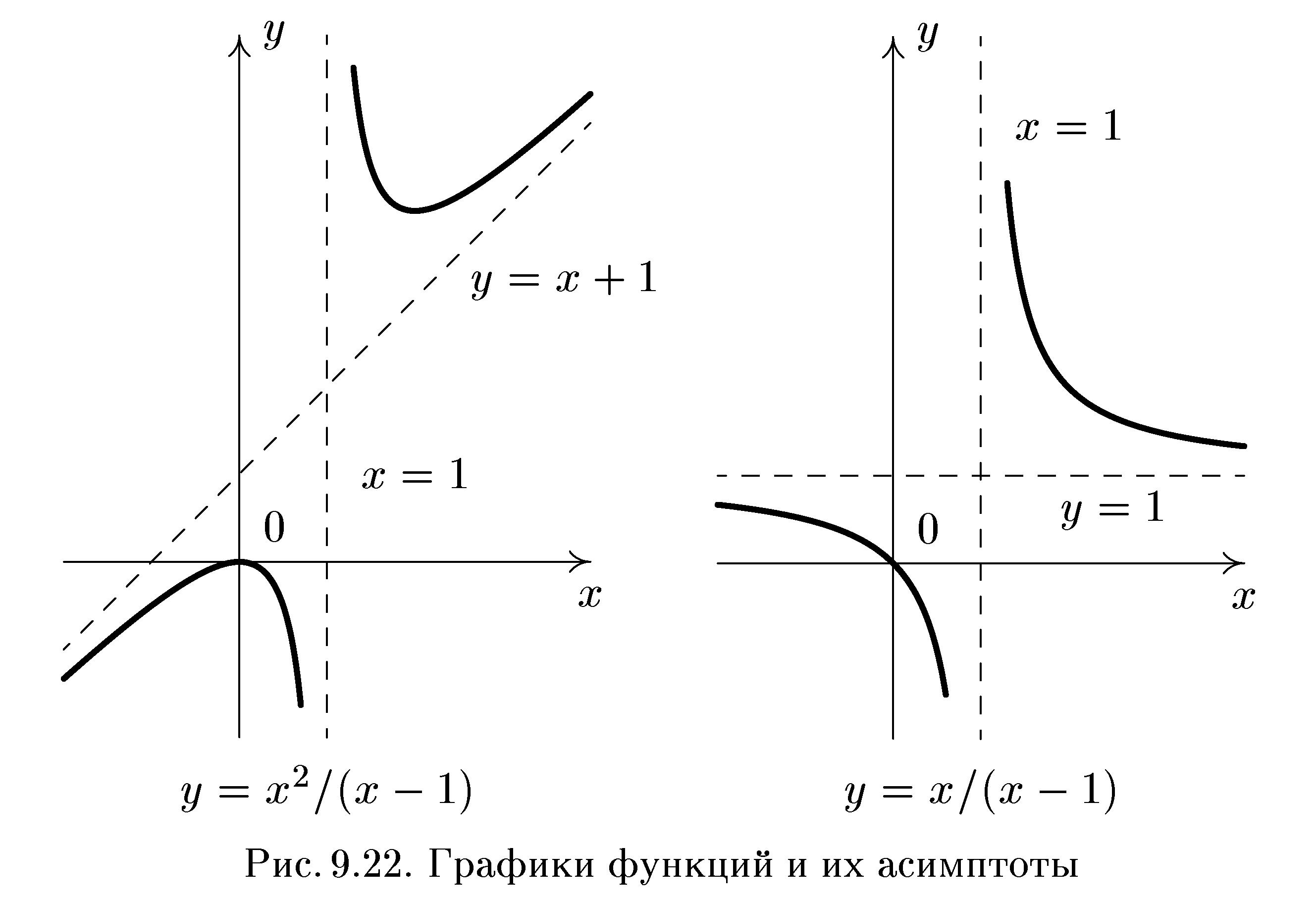
При построении графика функции важно правильно определить типы асимптот: горизонтальные, вертикальные или наклонные. Каждый тип асимптоты влияет на поведение функции в определенных областях.

Математический анализ, 15 урок, Ассимптоты

Для нахождения вертикальных асимптот необходимо искать значения x, при которых функция не определена, например, в точках разрыва или деления на ноль.
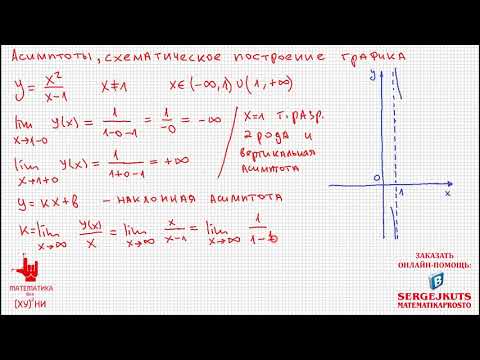
Математика без Ху%!ни. Нахождение асимптот, построение графика функции.

Горизонтальные асимптоты характеризуют поведение функции на бесконечности. Для их нахождения рассмотрите пределы функции при x, стремящемся к +∞ или -∞.

Асимптота, которая смогла - В интернете опять кто-то неправ #006 - Борис Трушин -


Наклонные асимптоты встречаются, когда функция стремится к прямой, но не горизонтальной, на больших значениях x. Их можно найти, вычислив предел отношения разности функции и прямой при x, стремящемся к бесконечности.

Асимптоты графика функции. Практика. Пример 1.


Не забывайте о возможных особенностях функций с разрывами или асимптоты могут быть не очевидны сразу, требуя более детального анализа.

Асимптоты графика функции (часть 1). Высшая математика.

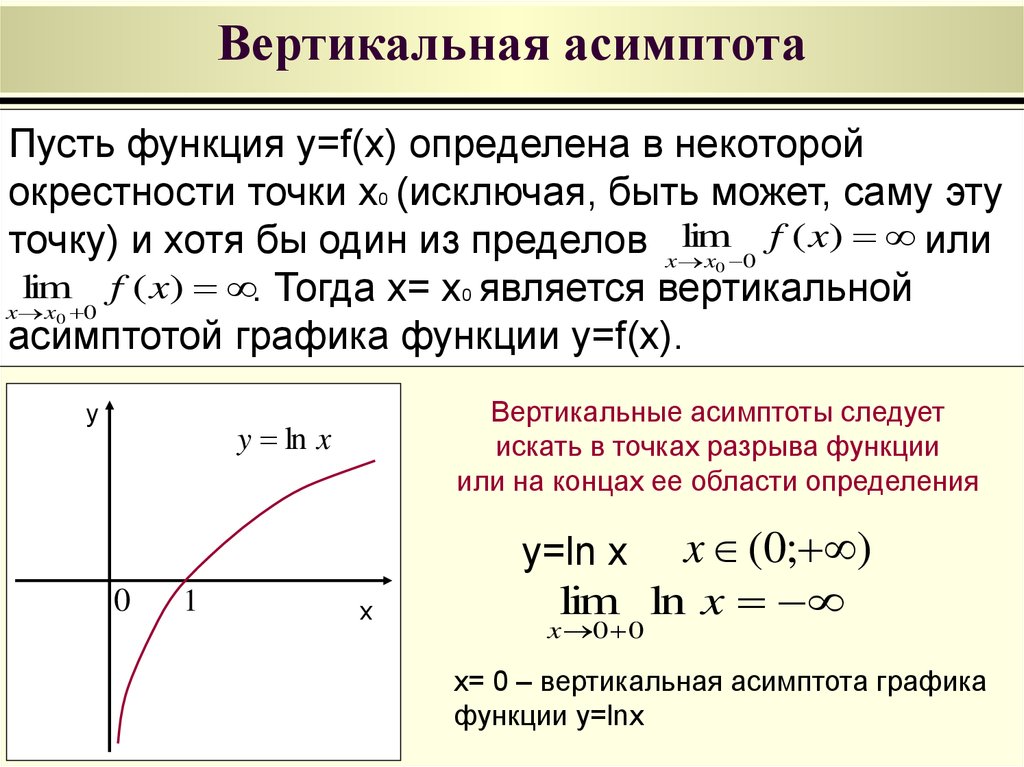
Для точности построения графика используйте соответствующие программные инструменты, такие как графопостроители или калькуляторы, чтобы визуализировать асимптоты и проверить результаты ваших вычислений.

Проверяйте асимптоты с помощью различных методов: аналитических (с помощью пределов) и графических (построение графика на компьютере или вручную).

Не забудьте учитывать возможное влияние асимптот на форму графика, так как они могут существенно изменить его вид в определенных областях.

При анализе асимптот часто полезно использовать разложение функции в ряд или приближенные методы для более точного понимания ее поведения.

Асимптоты функции. 10 класс.


Будьте внимательны к специфическим случаям, например, когда асимптоты могут пересекаться с графиком функции в ограниченных областях.
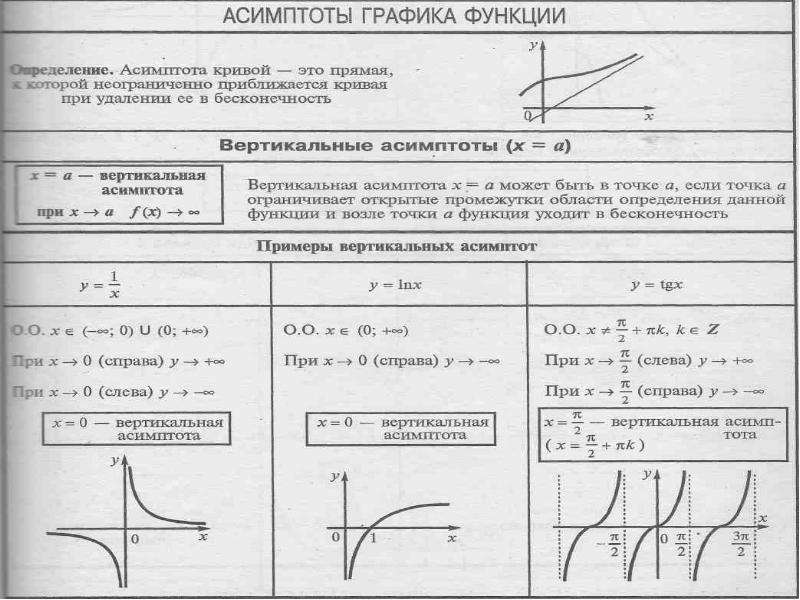
Математика без Ху%!ни. Исследование функции, график. Первая, вторая производная, асимптоты.