Как решать задачи с описанной окружностью вокруг треугольников: советы и рекомендации
Задачи на описанную окружность являются важной частью геометрии, требующей внимательного подхода. В этой подборке собраны ключевые моменты, советы и примеры для успешного решения задач, связанных с описанными окружностями около треугольников. Внимание к деталям, понимание теорем и использование основных свойств окружности помогут вам эффективно решать такие задачи.
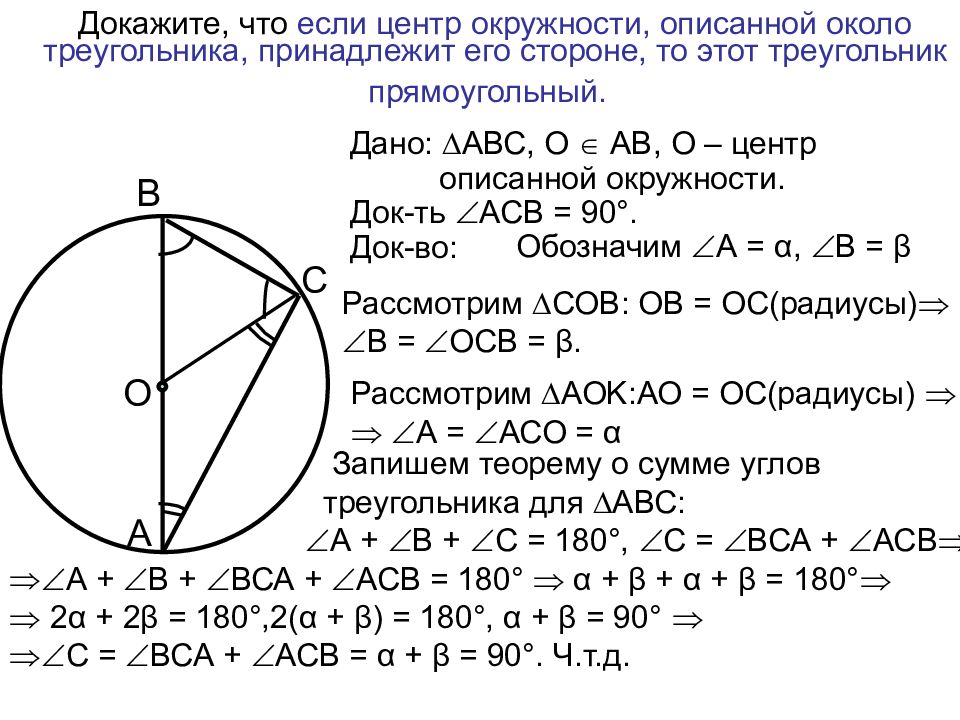
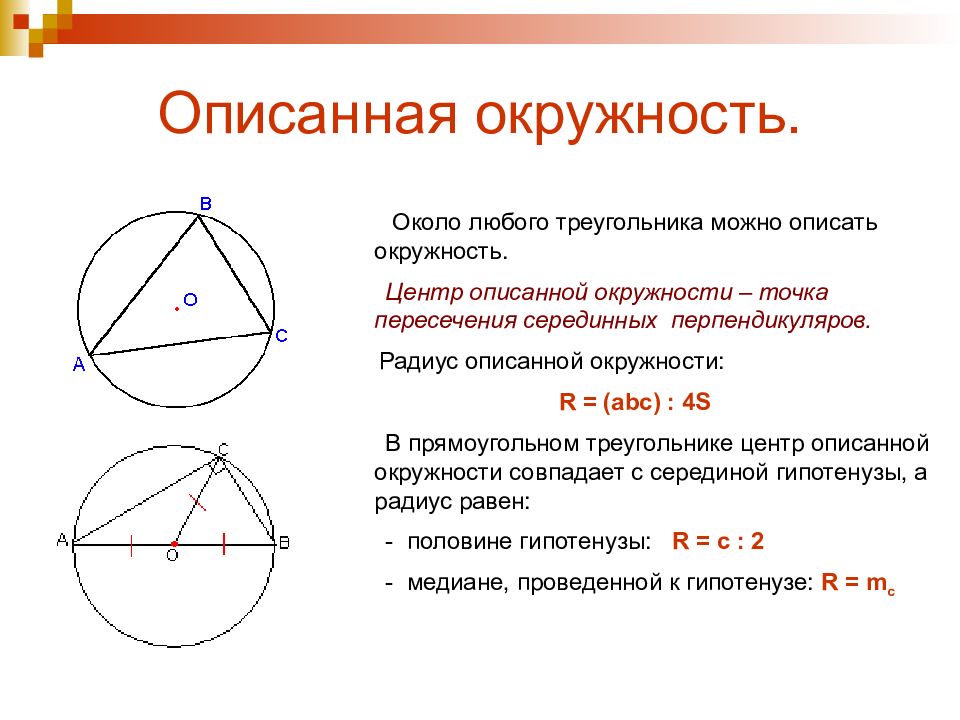
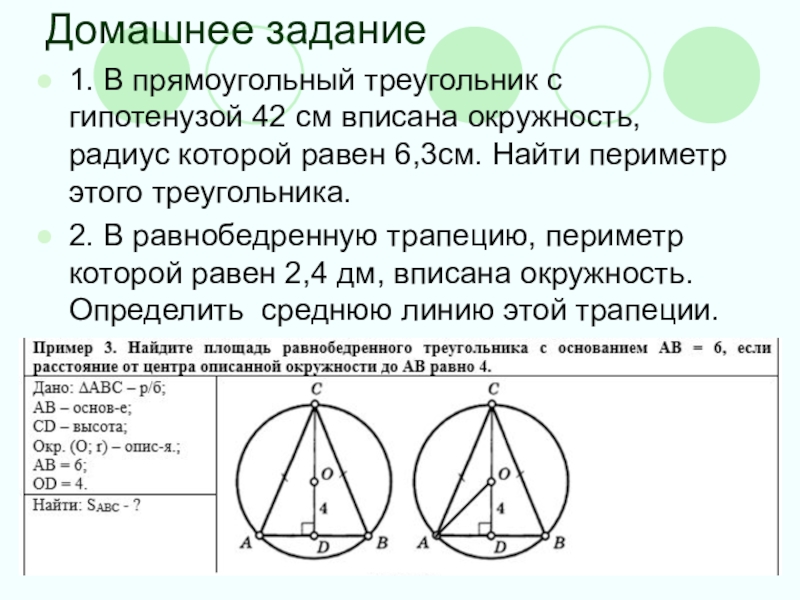
Начните с изучения теоремы о описанной окружности треугольника, она поможет вам лучше понять взаимосвязь сторон и углов треугольника с окружностью.

Окружность вписанная в треугольник и описанная около треугольника.

Не забывайте, что центр описанной окружности совпадает с точкой пересечения серединных перпендикуляров треугольника. Это важный факт для построений и доказательств.

РЕШЕНИЕ ЗАДАЧИ ПО ТЕМЕ «ОКРУЖНОСТЬ, ОПИСАННАЯ ОКОЛО ТРЕУГОЛЬНИКА». Задачи - ГЕОМЕТРИЯ 7 класс

Используйте формулы для нахождения радиуса описанной окружности, такие как R=abc4SR = /frac{abc}{4S}R=4Sabc, где a, b, c — стороны треугольника, а S — его площадь.

Окружность, описанная около likerkacinema.ru circumcircle of the triangle.
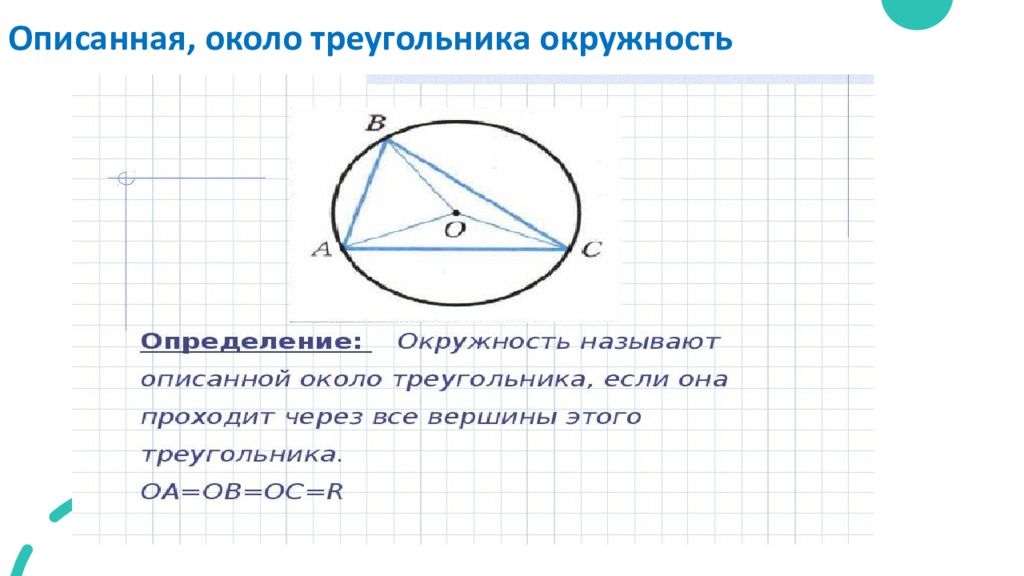
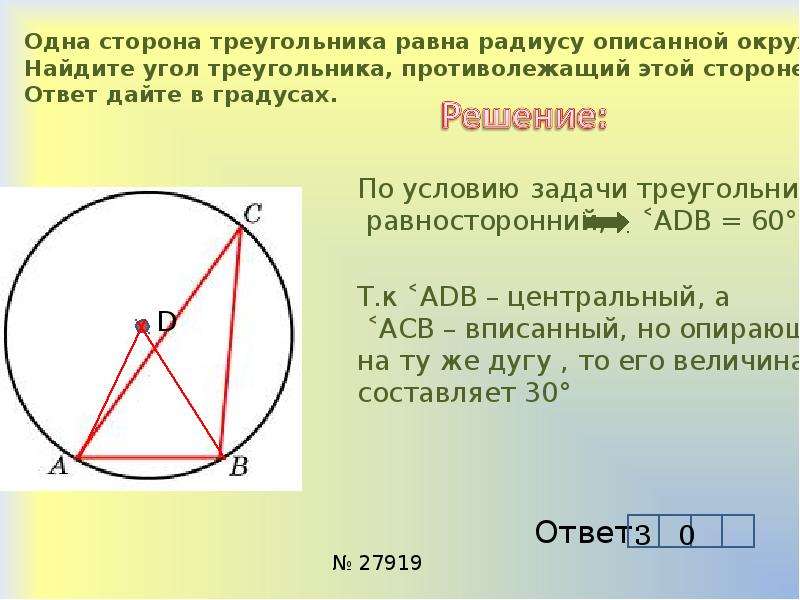
Для задач с углами полезно помнить, что углы при вершинах треугольника и их противоположные дуги на описанной окружности связаны через теорему о вписанных углах.
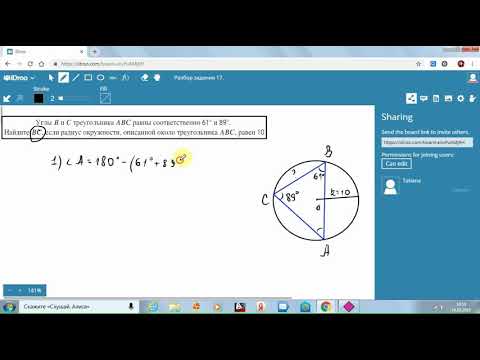
ОГЭ-2019. Задание 17. Теорема синусов, и описанная около треугольника окружность
При решении задач на описанную окружность часто возникает необходимость использования свойств хорды и дуг окружности. Не забывайте о связи между длиной хорды и углом, который она образует с центром окружности.

ОГЭ. Задача на описанную окружность № 16. Как легко решить задачу
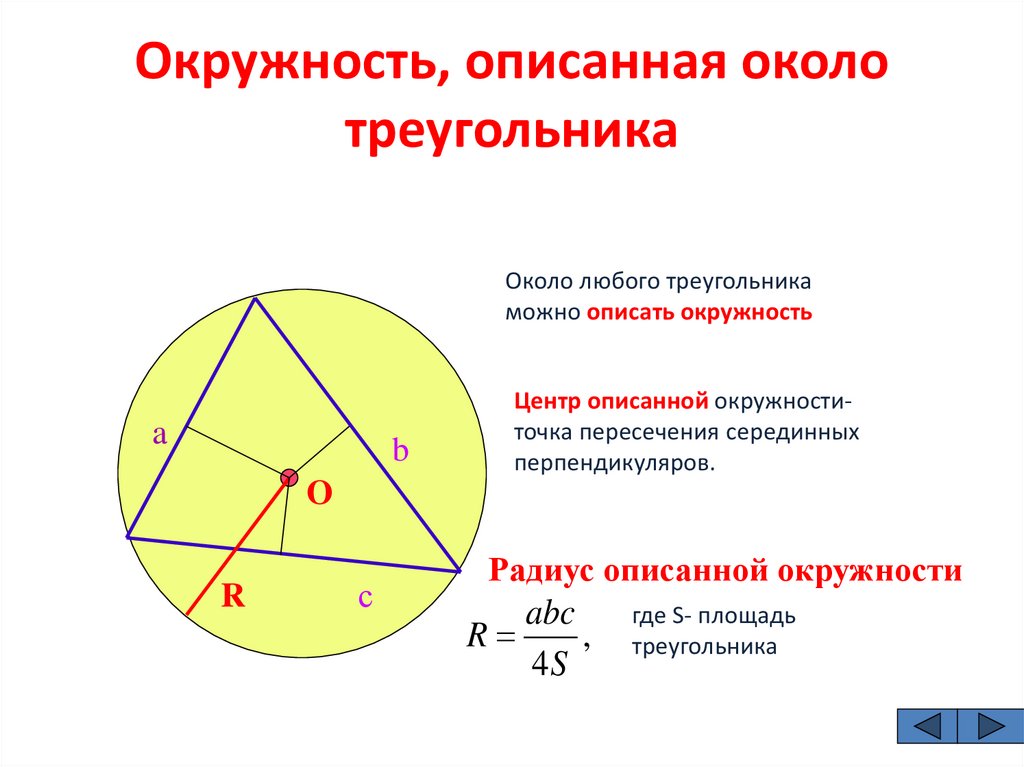

В задачах с прямыми углами можно применить теорему Пифагора для нахождения радиуса описанной окружности, если один из углов треугольника является прямым.

Вписанная и описанная окружности - Лайфхак для запоминания
Внимательно читайте условия задач, чтобы понять, какая информация о треугольнике дана напрямую, а какую нужно вычислять с помощью теорем и формул.
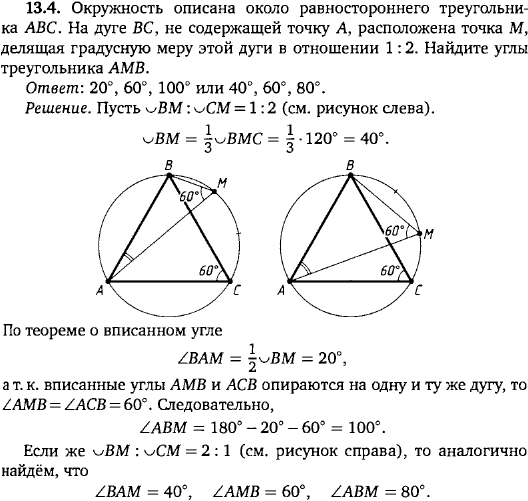

Использование симметрии треугольников поможет упростить решение задач с описанными окружностями, особенно если треугольник является равнобедренным или равносторонним.

Построить описанную окружность (Задача 1)
Если задача требует нахождения длины дуги окружности, используйте формулы для вычисления дуги на основе угла между радиусами и длины стороны треугольника.
На экзаменах и контрольных всегда проверяйте свои решения, строя диаграммы для наглядного понимания расположения описанных окружностей и их свойств.
