Что такое вписанный угол и как его использовать
Вписанный угол — это один из ключевых элементов геометрии окружности. В этой статье вы найдете простое объяснение, наглядные примеры и полезные советы для изучения и применения этой темы.

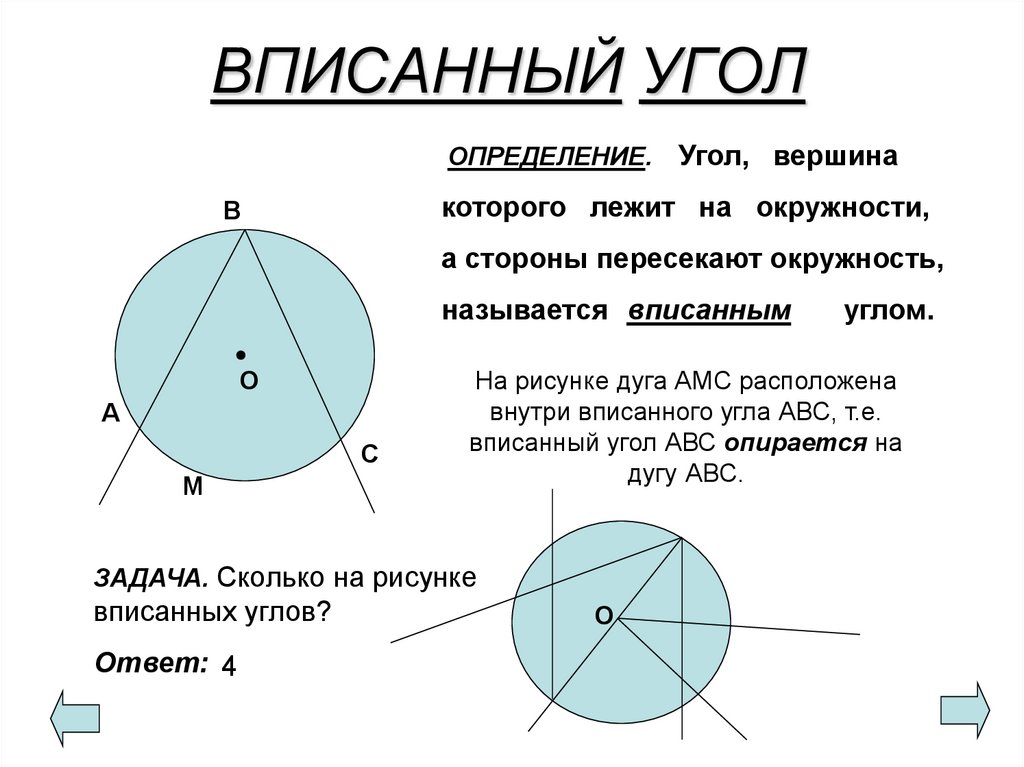
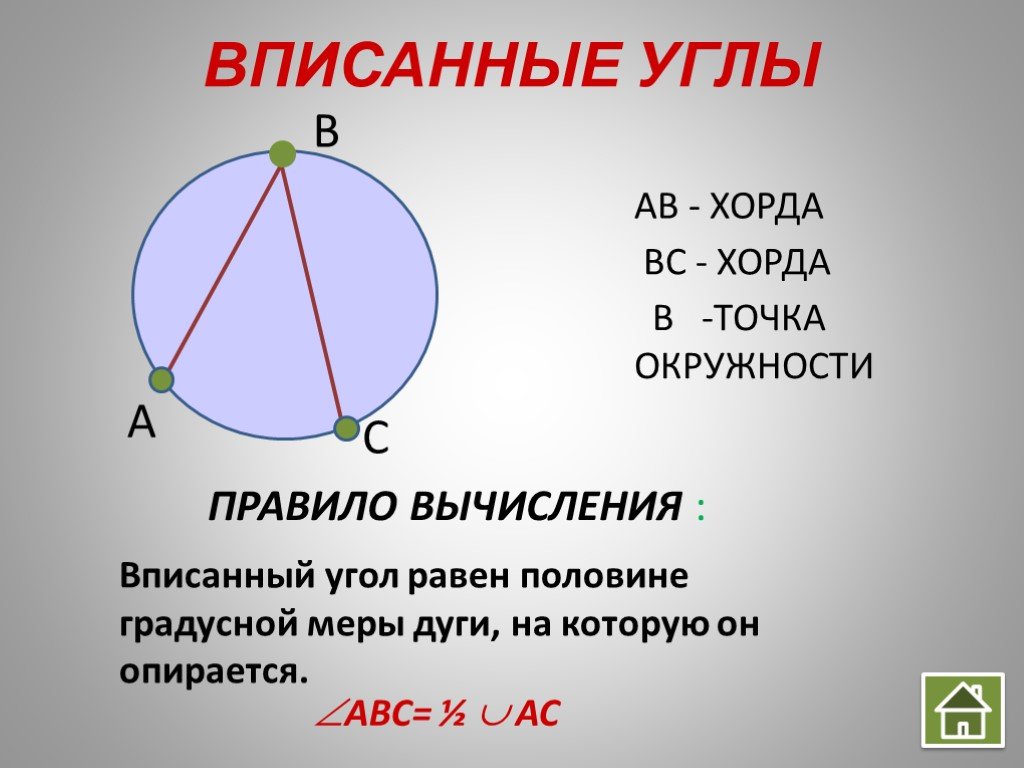
Всегда проверяйте, что вершина вписанного угла лежит на окружности.

ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный Угол
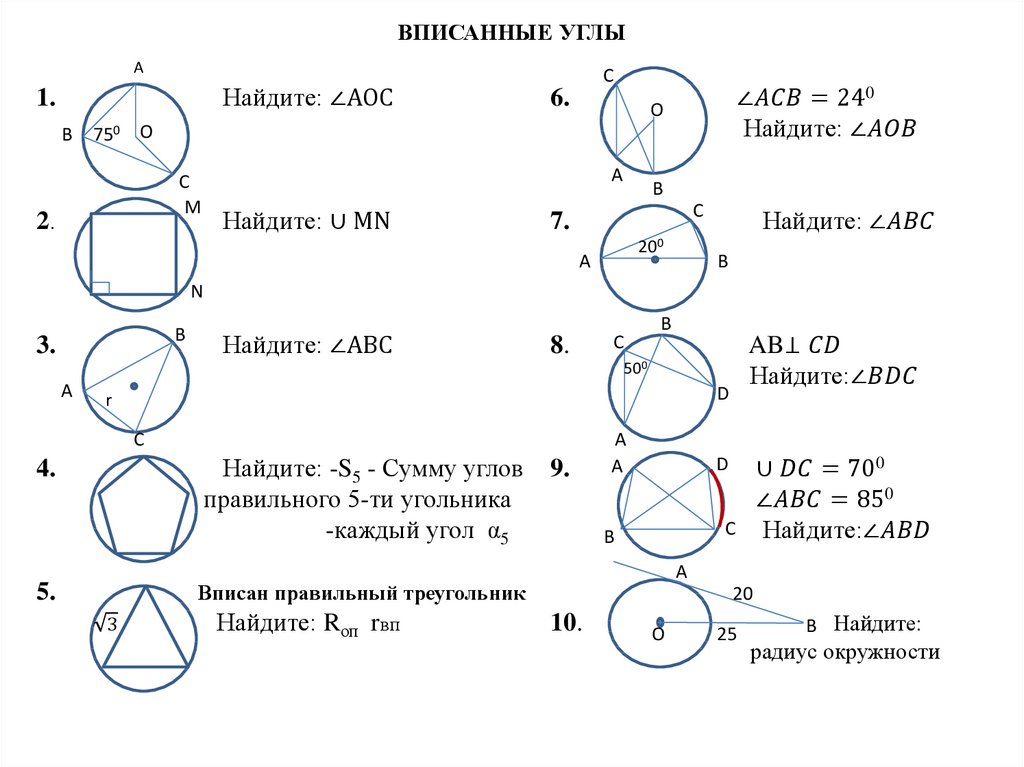
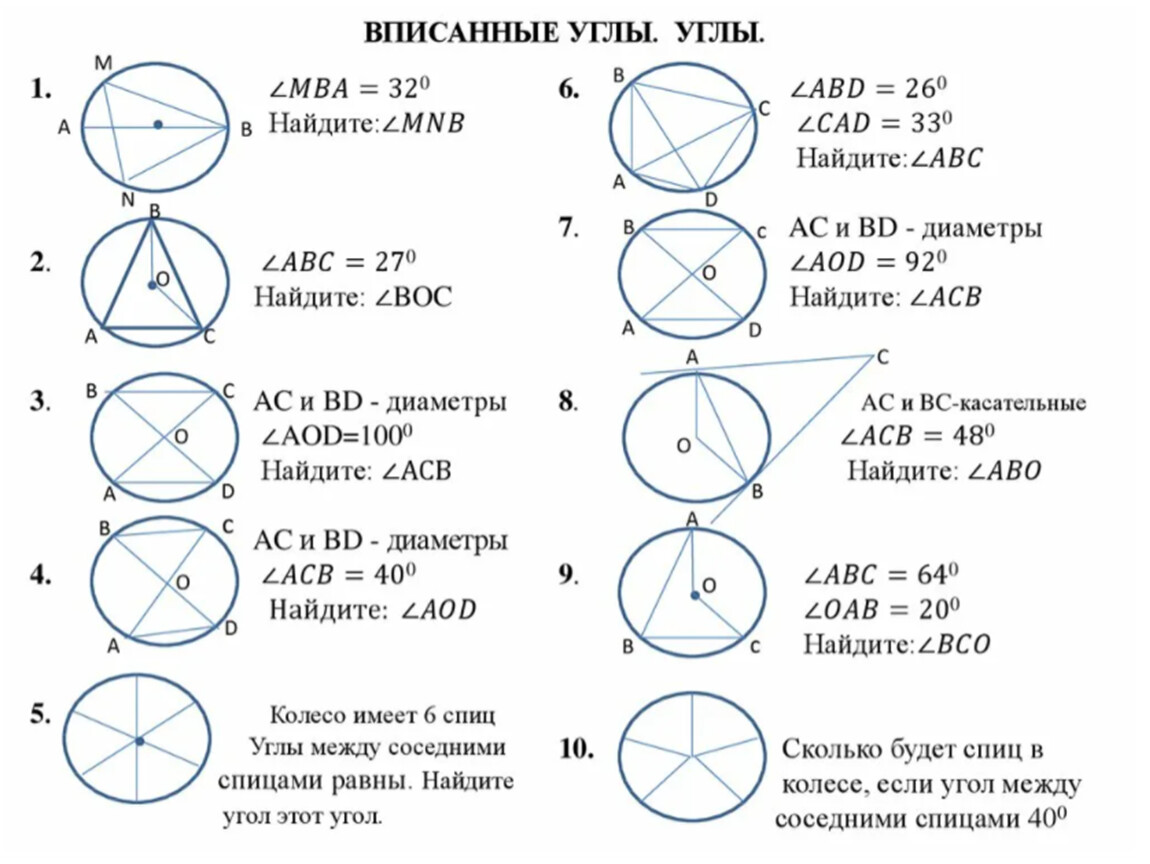
Помните, что вписанный угол равен половине соответствующего центрального угла.

Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСС

Используйте вписанные углы для доказательства равенства углов в задачах на окружностях.

Всё про вписанные и центральные углы за 4 минуты - Борис Трушин -
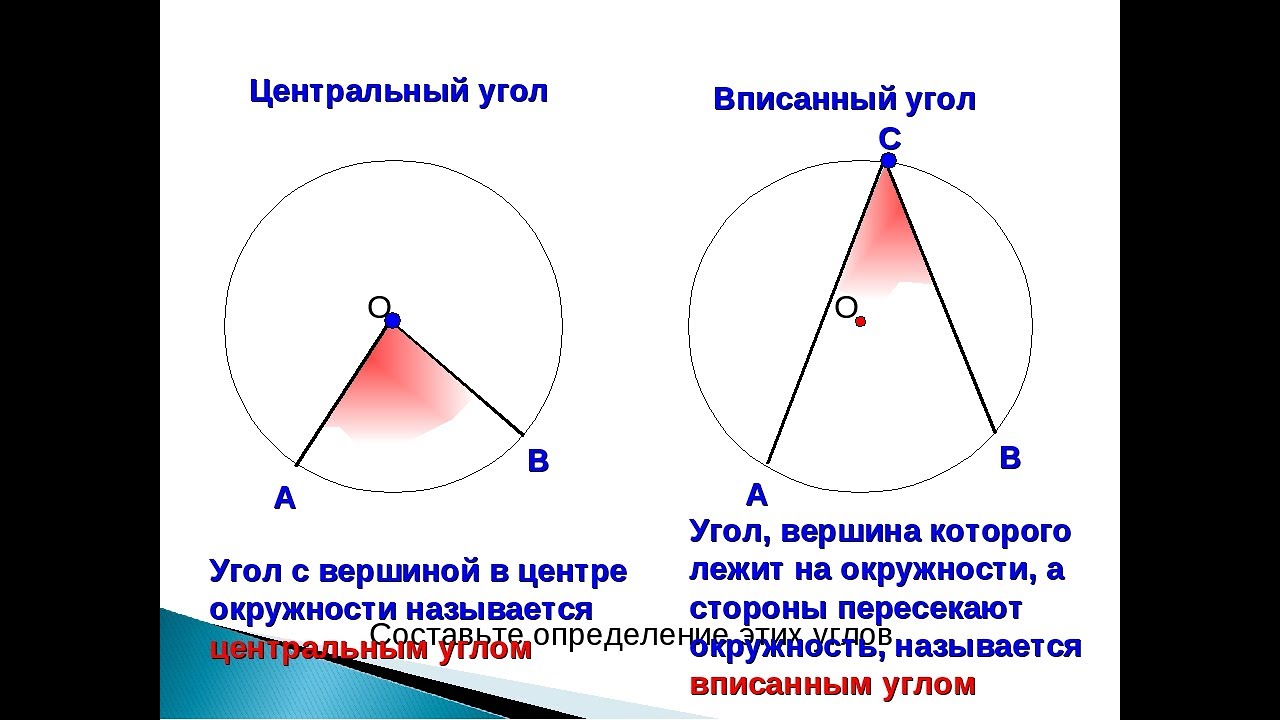
При решении задач начертите окружность и выделите все известные элементы.

Вписанные углы в окружности

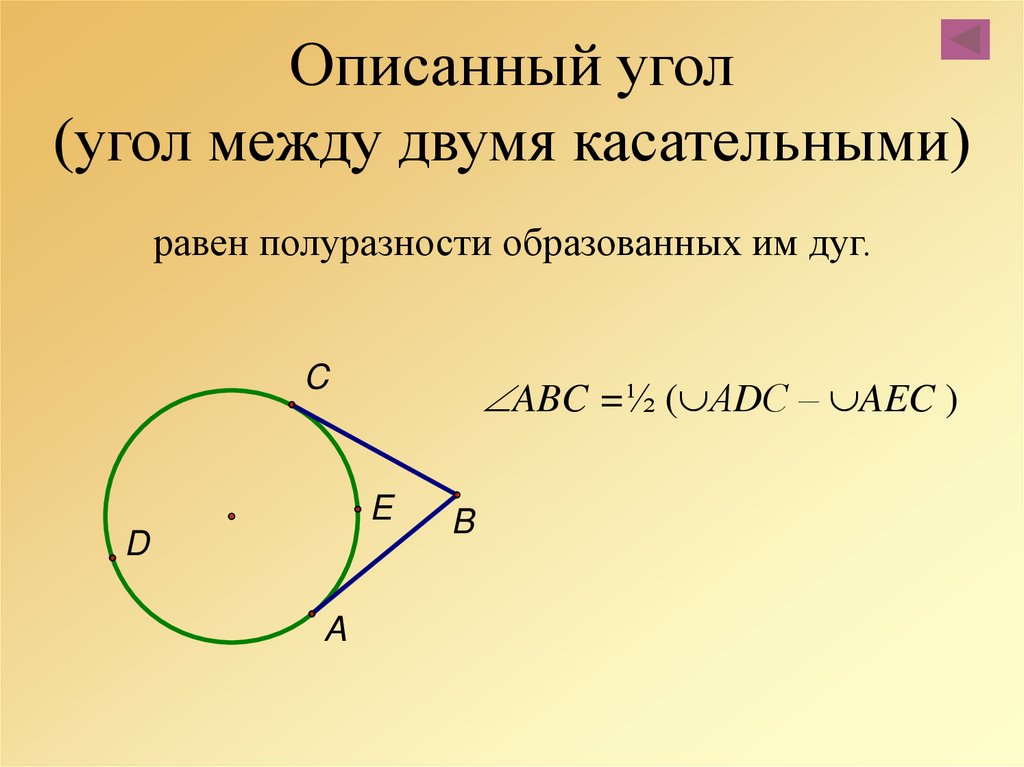
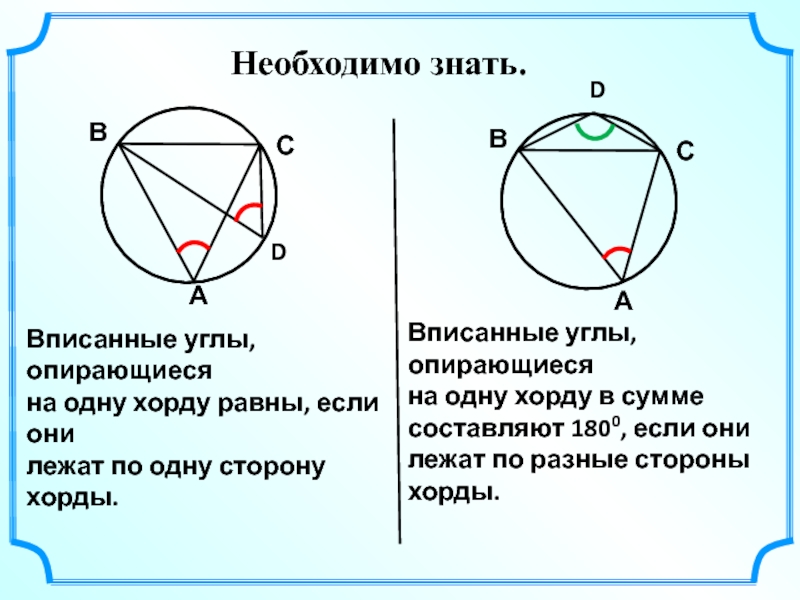
Знайте, что все вписанные углы, опирающиеся на одну и ту же дугу, равны.

Всё про углы в окружности. Геометрия - Математика
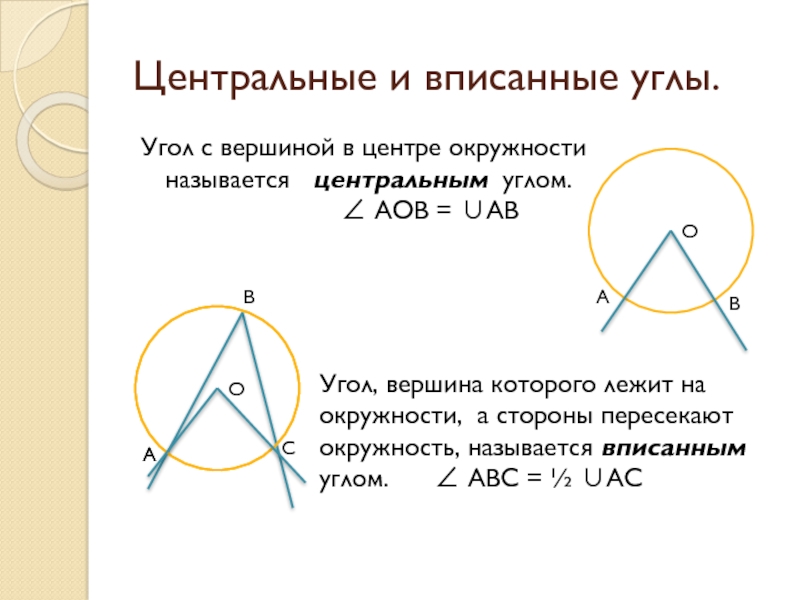
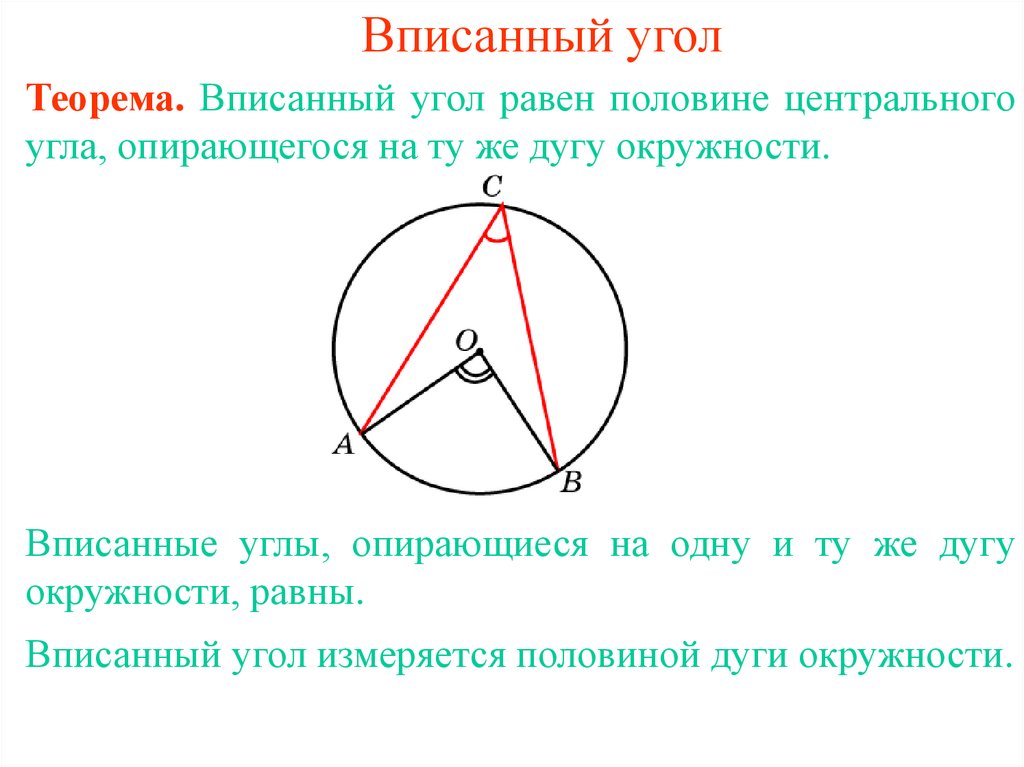
Используйте свойства вписанных углов при вычислении длины дуги или площади сектора.

ДЕМОВЕРСИЯ ОГЭ 2025 по математике - РАЗБОР 2 ЧАСТИ ОГЭ ПО МАТЕМАТИКЕ 2025 - 99 баллов
Обратите внимание, что вписанный угол, опирающийся на диаметр, всегда прямой.
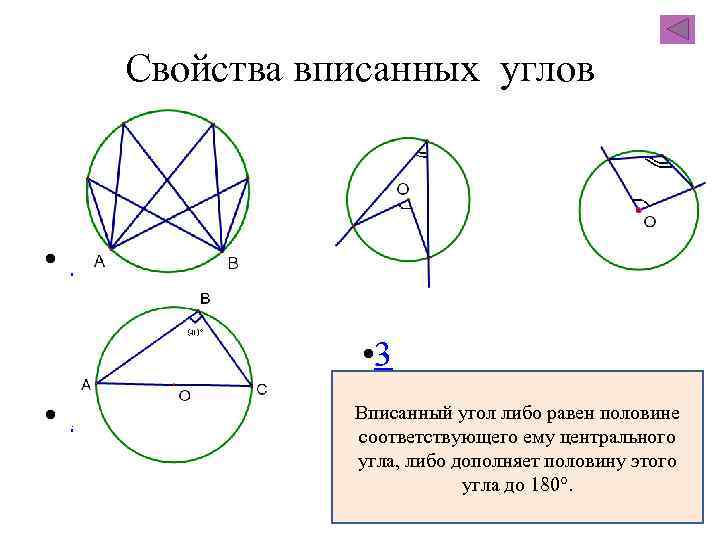
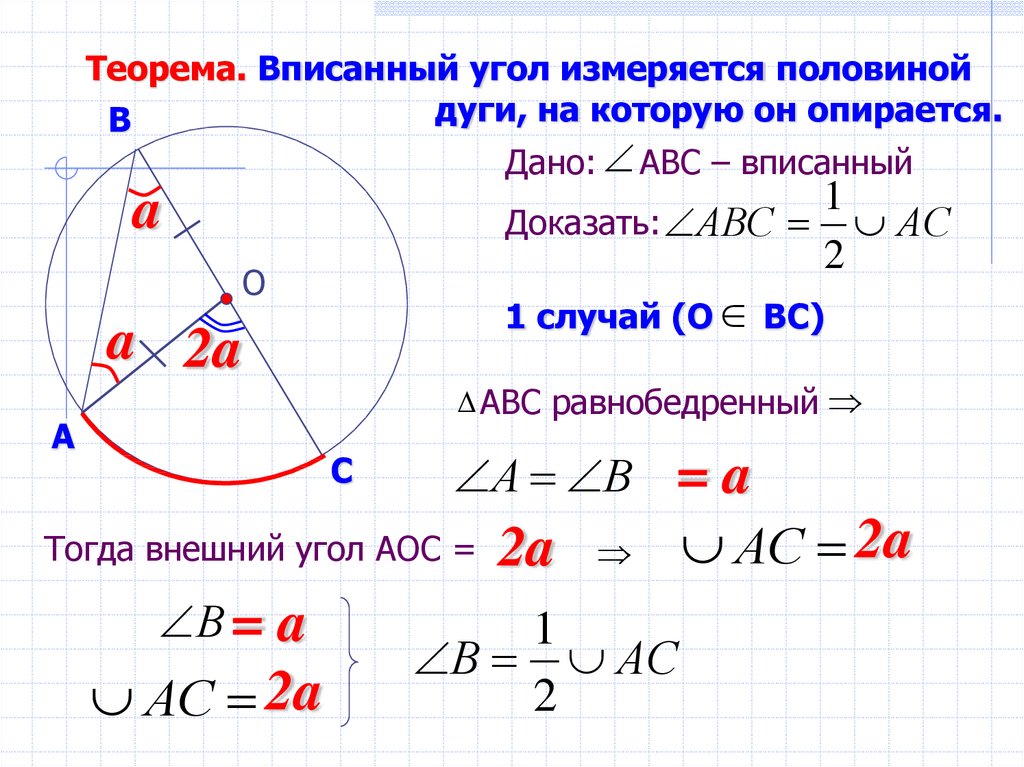
Для задач с вписанными четырёхугольниками помните, что сумма противоположных углов равна 180°.

Вписанные углы: вокруг ортоцентра
В задачах с окружностями полезно помнить формулу длины дуги через вписанный угол.
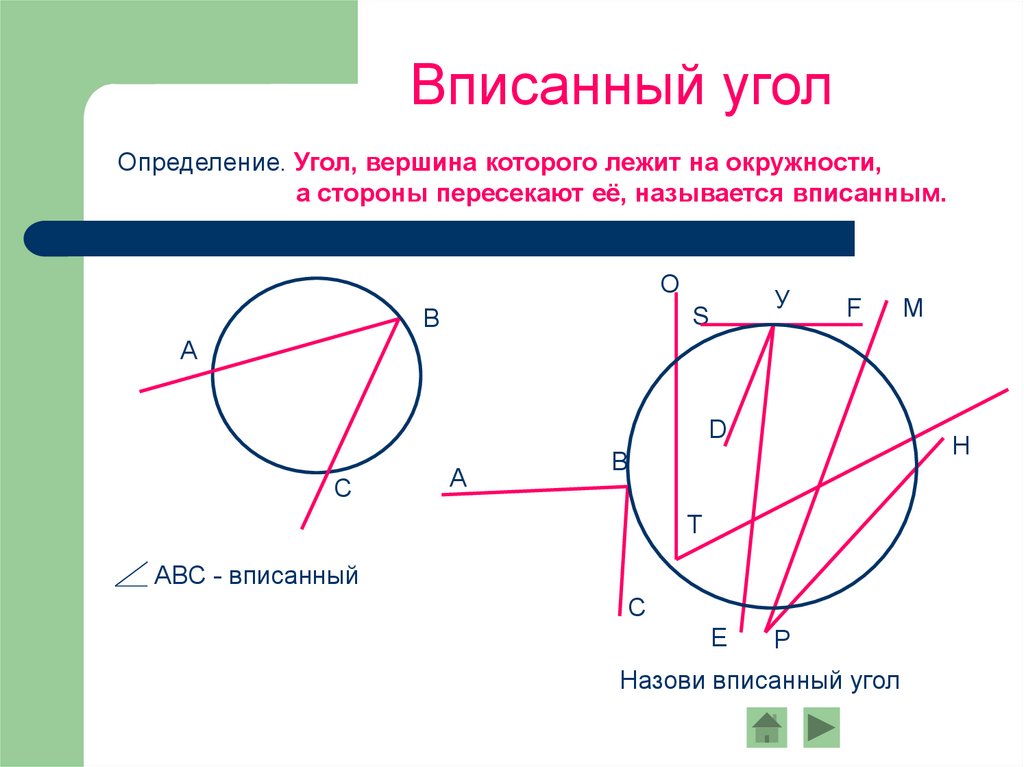

Если есть трудности, начните с простых чертежей для наглядности.

ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ . §9 геометрия 8 класс
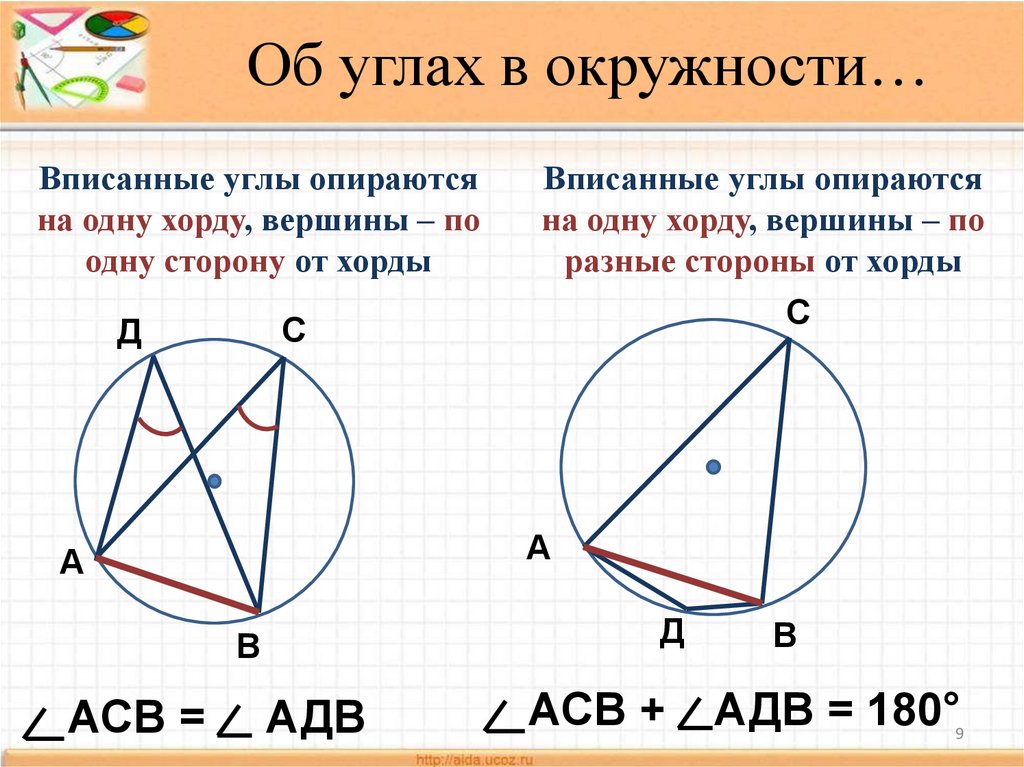

Углы, вписанные в окружность. 9 класс.