Основные принципы возрастания функции и практические советы для изучающих
Возрастание функции — это один из фундаментальных понятий в математике, особенно в анализе. Оно описывает, как меняется значение функции по мере изменения её аргумента. Понимание этого процесса важно не только для теории, но и для практического применения в различных областях науки и техники. Здесь вы найдете полезные советы и рекомендации, которые помогут глубже разобраться в этой теме и улучшить ваши навыки работы с функциями.

Чтобы понять возрастание функции, начните с анализа её графика. Это поможет визуально оценить, как меняется её значение.
10 класс, 44 урок, Применение производной для исследования функций на монотонность и экстремумы

Не забывайте про производную функции — если она положительна, то функция возрастает, если отрицательна — убывает.

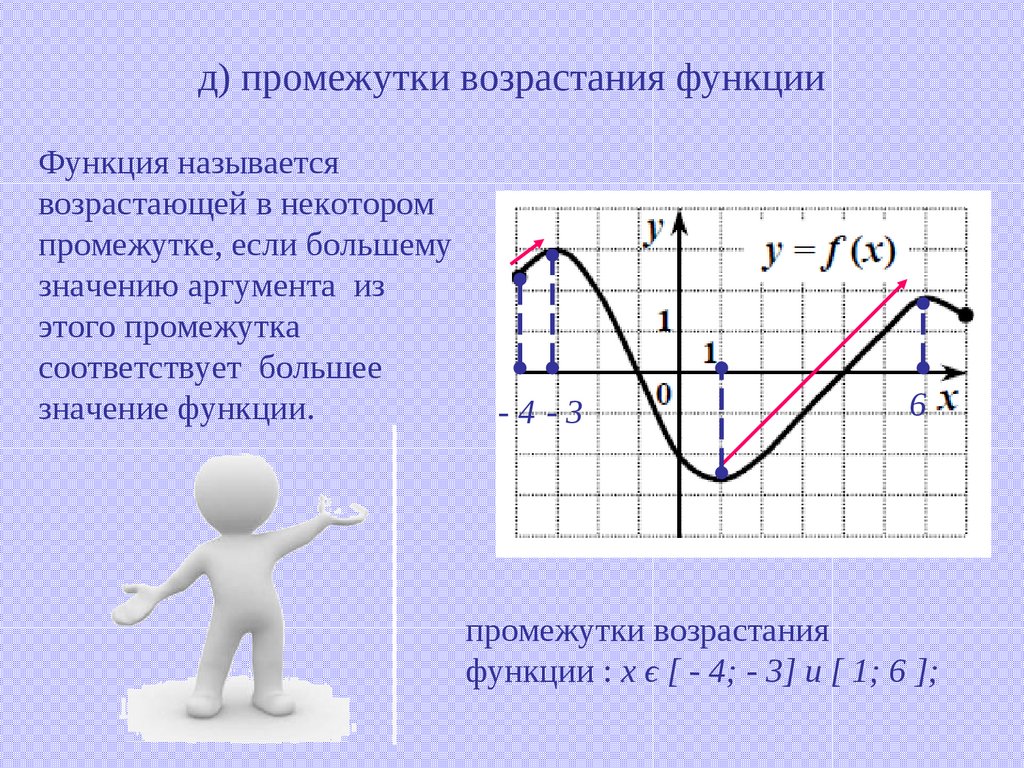
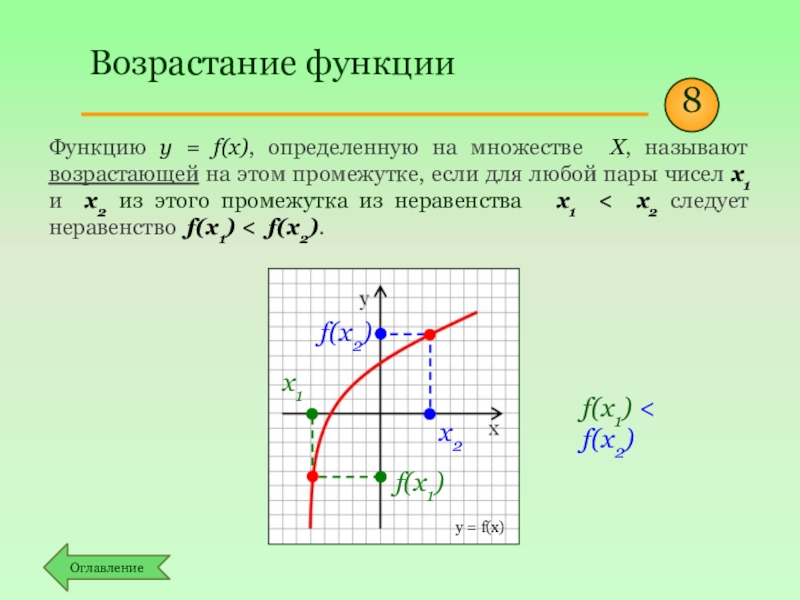
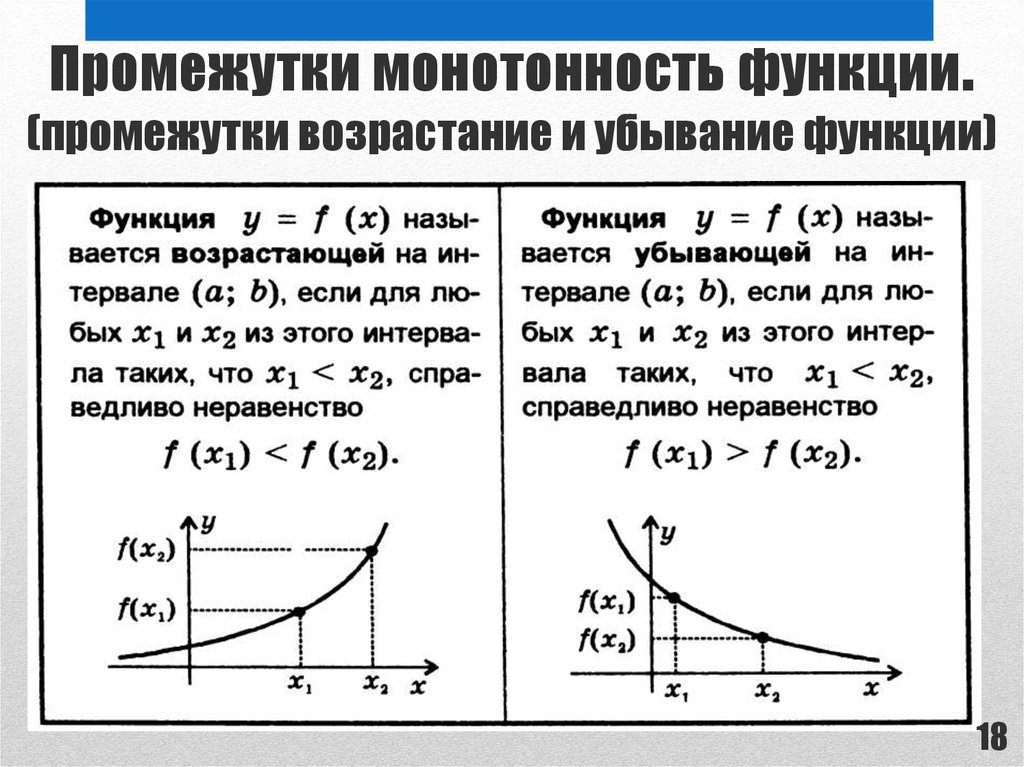
Возрастание и убывание функции
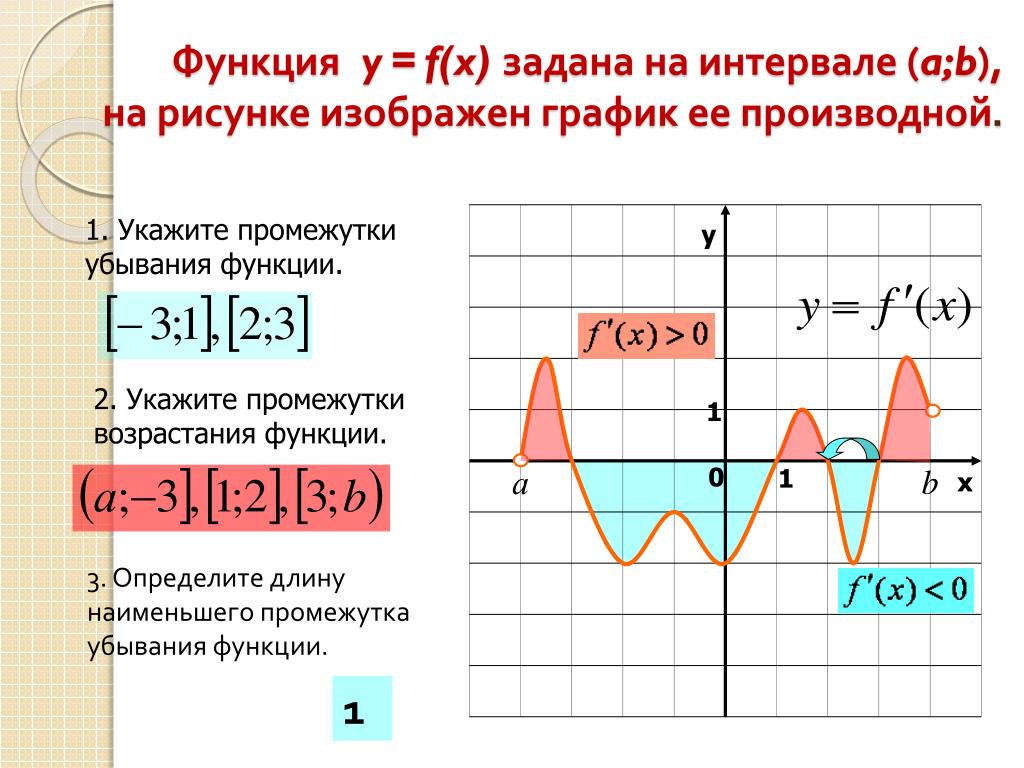
При исследовании функции на возрастание или убывание важно учитывать её критические точки и интервалы, на которых производная меняет знак.
Возрастание функции - убывание функции - 9 класс Макарычев

Для практических целей можно использовать численные методы для нахождения максимума и минимума функции.

Свойства функции. Возрастание и убывание. Как определить по графику и записать правильно. 7-11 класс

Исследуя поведение функции, всегда проверяйте её асимптоты, так как они могут повлиять на восприятие возрастания на больших значениях аргумента.
Свойства функции. Промежутки возрастания и убывания функции. 10 класс.

Когда изучаете сложные функции, разделите их на более простые компоненты и анализируйте каждую часть отдельно.
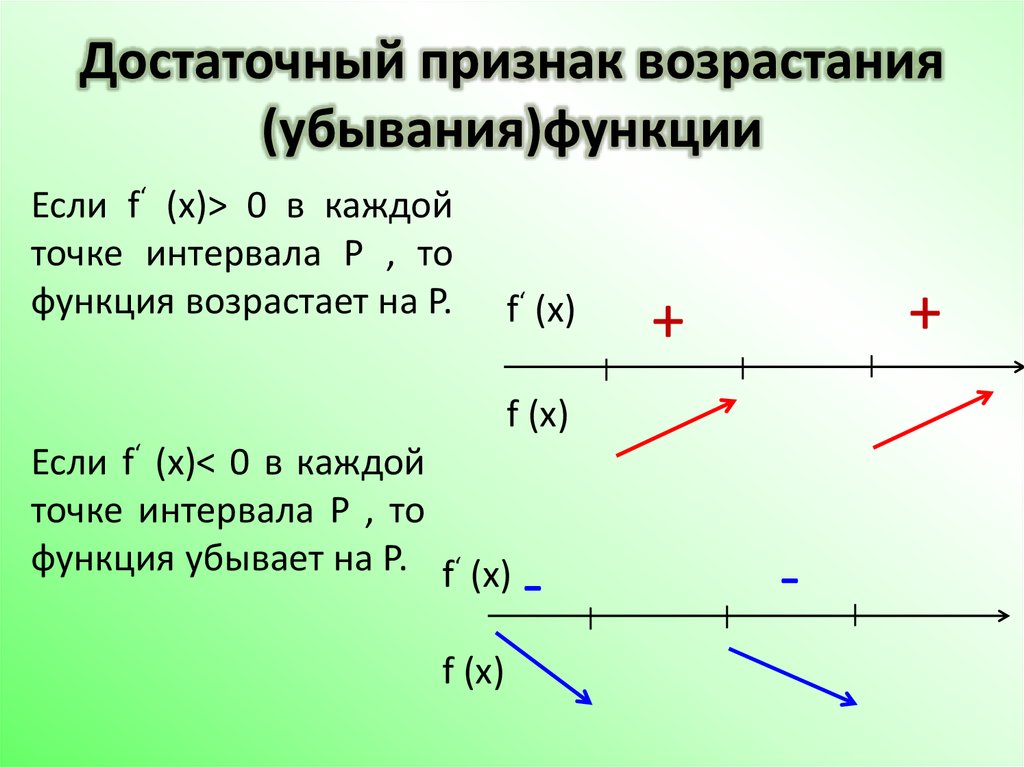
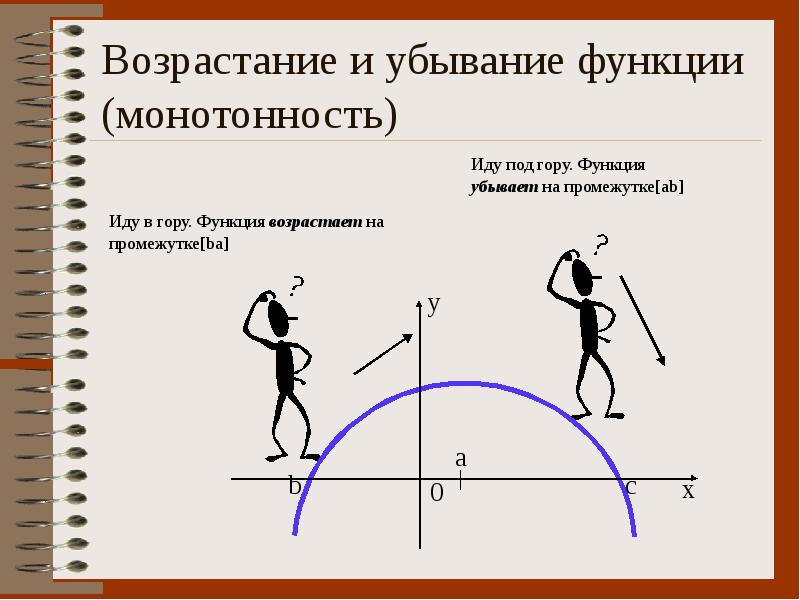
Используйте таблицы знаков для более удобного нахождения интервалов возрастания и убывания функции.

ТОЧКА МАКСИМУМА И МАКСИМУМ ФУНКЦИИ ЧАСТЬ I #математика #егэ #огэ #shorts #геометрия
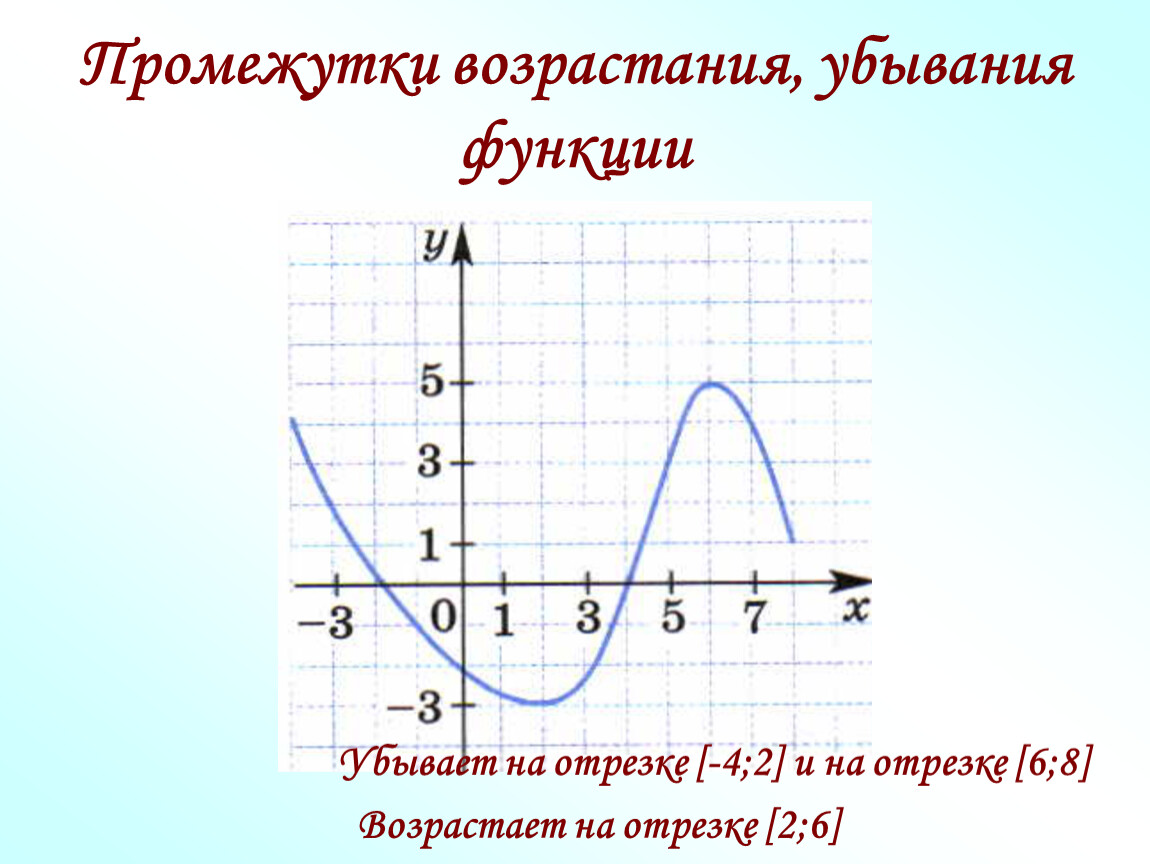
Не забывайте, что монотонность функции может быть ограничена её доменом, поэтому важно учитывать возможные ограничения на область определения.
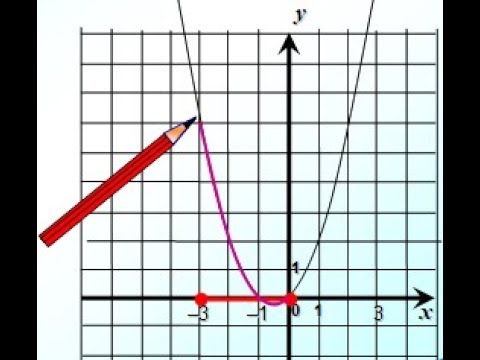
Задание 10 Возрастание убывание функции
Для точного анализа возрастания функции используйте производные высших порядков, особенно в сложных случаях.
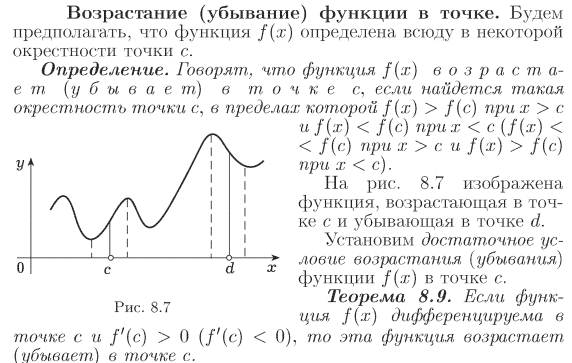
Практикуйтесь на реальных примерах, чтобы лучше понять, как возрастание функции используется в решении прикладных задач.

Возрастание и убывание функции от bezbotvy