Как найти объем тела, заключенного между параболоидом и сферой, с примерами решений

Этот материал посвящен вычислению объема тела, ограниченного параболоидом и сферой. Мы подробно разберем подходы к решению задачи, рассмотрим математические методы и основные этапы вычислений, а также дадим полезные советы для успешного выполнения подобных расчетов.

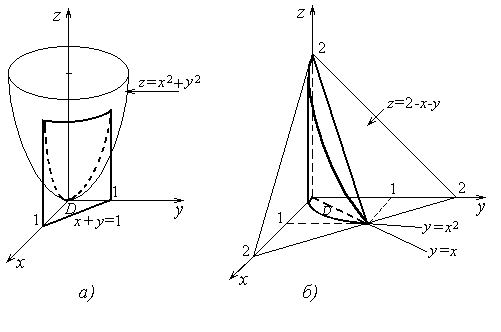
Начните с правильной постановки задачи и уточните границы тела, которые ограничены параболоидом и сферой, чтобы избежать ошибок при вычислениях.

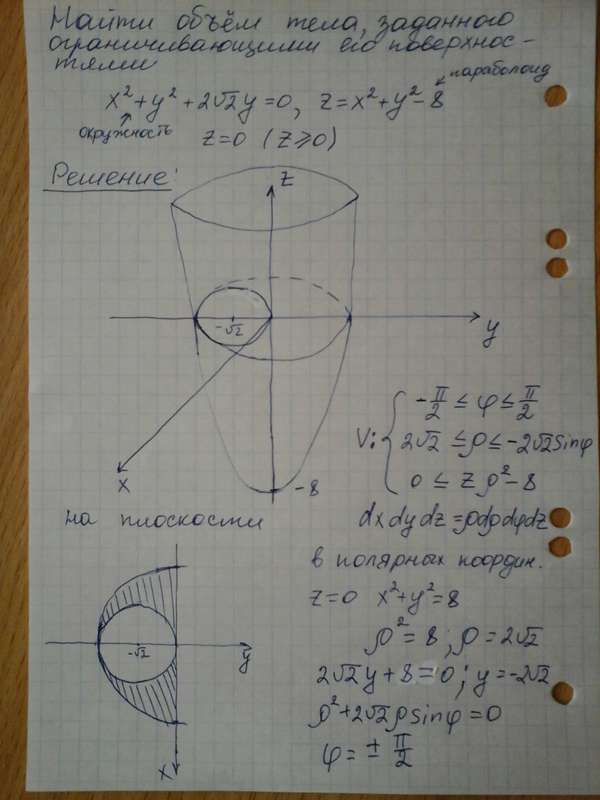
Используйте координатную систему, которая лучше всего подходит для описания геометрии тела, например, сферические или цилиндрические координаты.

Обратите внимание на возможные симметрии тела, что может существенно упростить вычисления и уменьшить количество операций.

При вычислениях объема часто используется метод интегрирования. Убедитесь, что правильно выбрали пределы интегрирования для каждой из переменных.

Не забывайте, что параболоид и сфера могут пересекаться в нескольких точках, поэтому важно правильно определить их пересечение для корректного вычисления объема.

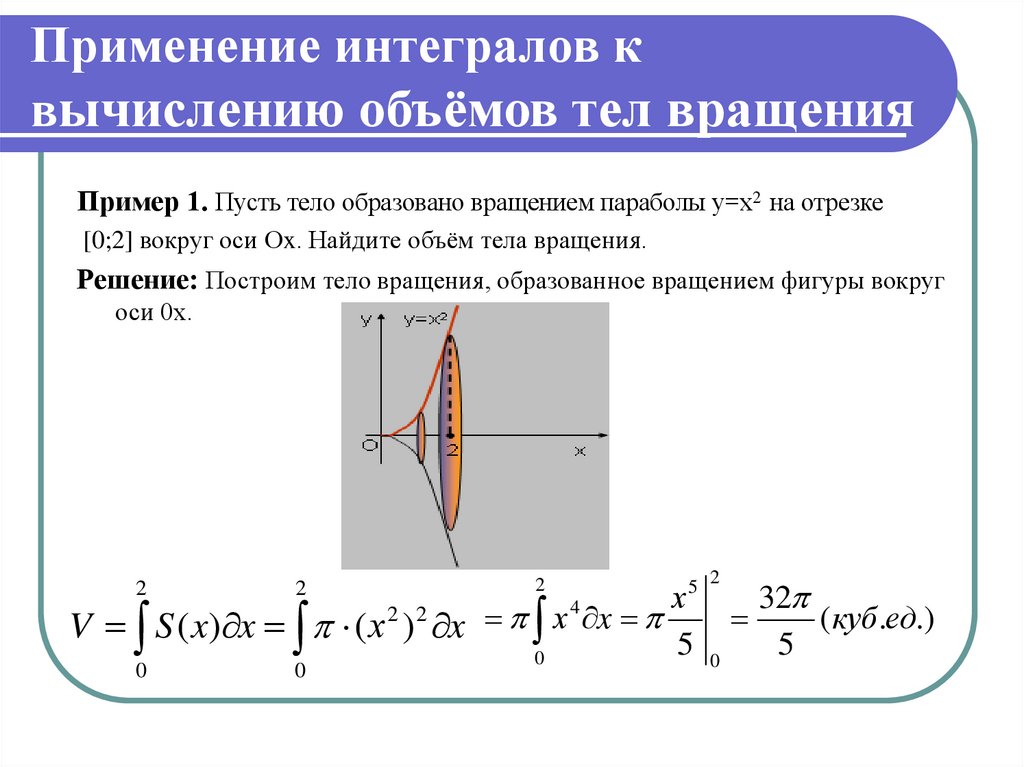
Для удобства расчета объема можно разделить тело на несколько частей, если его геометрия сложна.

Используйте численные методы интегрирования, если аналитическое решение задачи невозможно или слишком громоздко.

Проверьте единицы измерения при расчетах, чтобы убедиться, что они согласованы и результат будет в нужных единицах объема.

Если задача вызывает трудности, попробуйте использовать графическое представление тела, чтобы лучше понять его форму и границы.

При решении задач на объем всегда проверяйте промежуточные результаты, чтобы не допустить арифметических ошибок, особенно при сложных интеграциях.