Векторное произведение и его применение для нахождения площади: советы и рекомендации
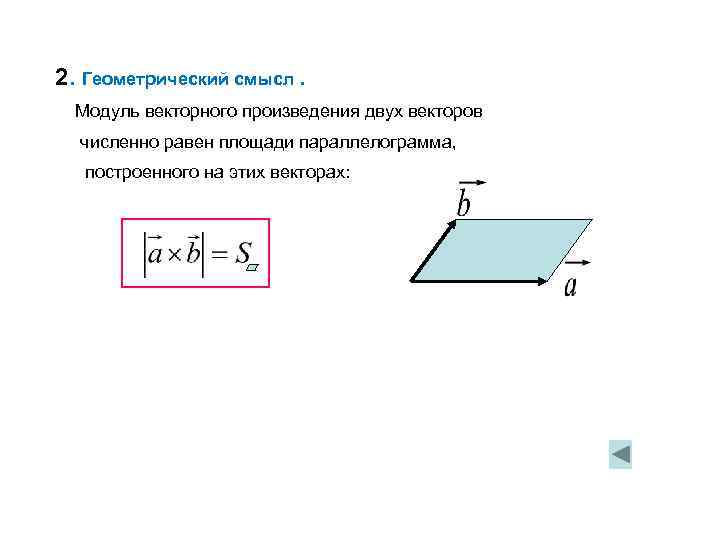
Векторное произведение – важный инструмент в геометрии и физике, который позволяет вычислять площади различных фигур, таких как параллелограмм и треугольники. В этом руководстве вы найдете основные принципы работы с векторным произведением и полезные советы для практических задач.
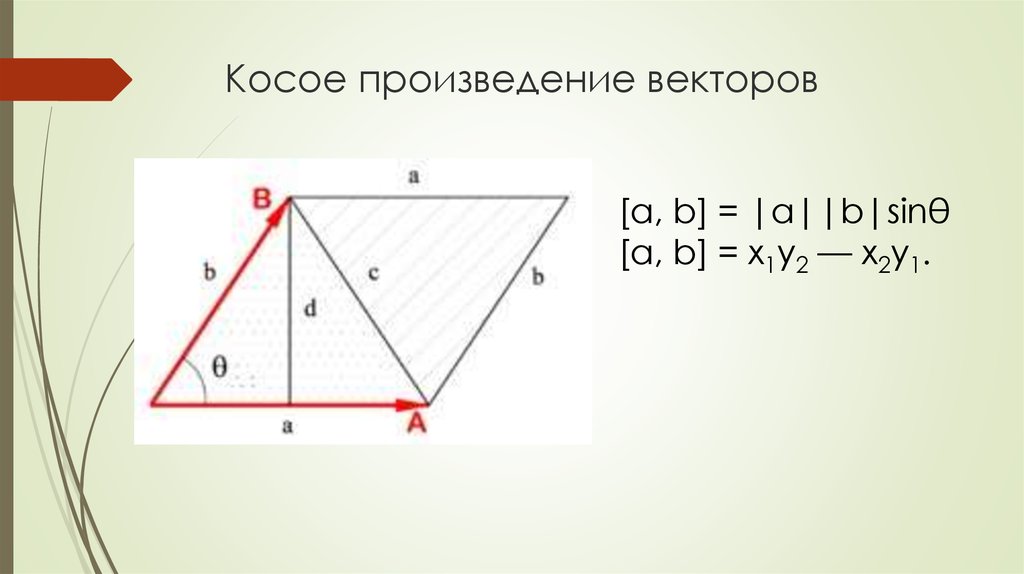
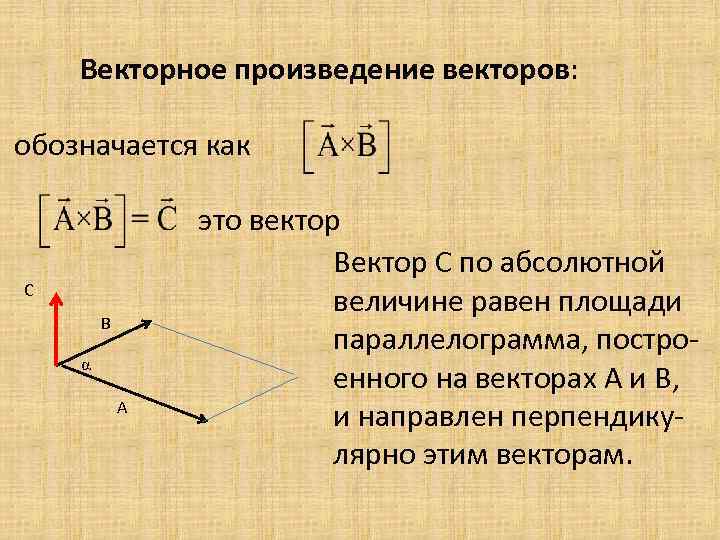
Для нахождения площади параллелограмма используйте формулу: S = |A × B|, где A и B – векторы, образующие стороны параллелограмма.

18+ Математика без Ху%!ни. Векторное произведение.
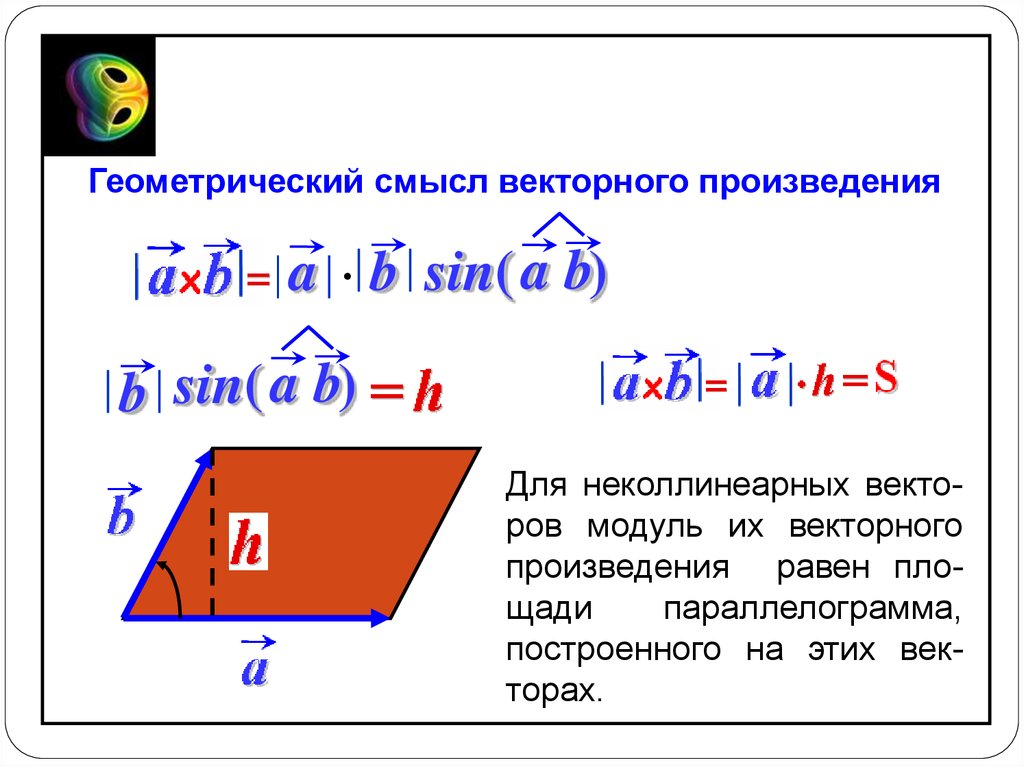

Для вычисления площади треугольника, возьмите половину площади параллелограмма: S = 0.5 × |A × B|, где A и B – стороны треугольника.
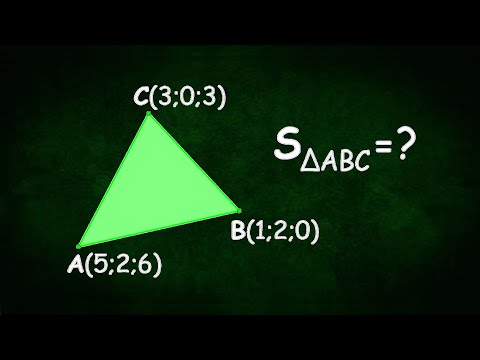
Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)

Не забывайте, что векторное произведение двух векторов всегда перпендикулярно к плоскости, в которой они лежат, что помогает понять геометрическую интерпретацию результата.

Векторное произведение - Сущность Линейной Алгебры, Глава 8

При работе с векторным произведением важно помнить, что порядок векторов имеет значение: A × B ≠ B × A, а их произведение противоположно по направлению.
Векторное произведение
Векторное произведение можно вычислять как детерминант матрицы, составленной из координат векторов. Это дает возможность быстро решать задачи с числовыми данными.

Решение, найти площадь треугольника, построенного на векторах a и b пример 8 Высшая математика
Для векторов в 3D пространстве используйте формулу: A × B = (A2B3 - A3B2, A3B1 - A1B3, A1B2 - A2B1), где A1, A2, A3 и B1, B2, B3 — компоненты векторов.

Векторное произведение векторов


Векторное произведение можно применять не только для нахождения площади, но и для определения ориентации векторов в пространстве.

Векторное произведение векторов - Высшая математика
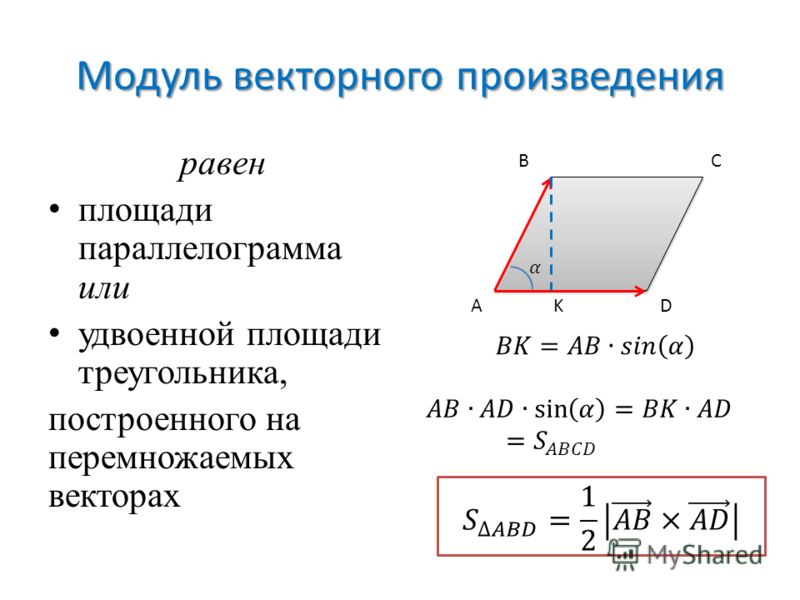
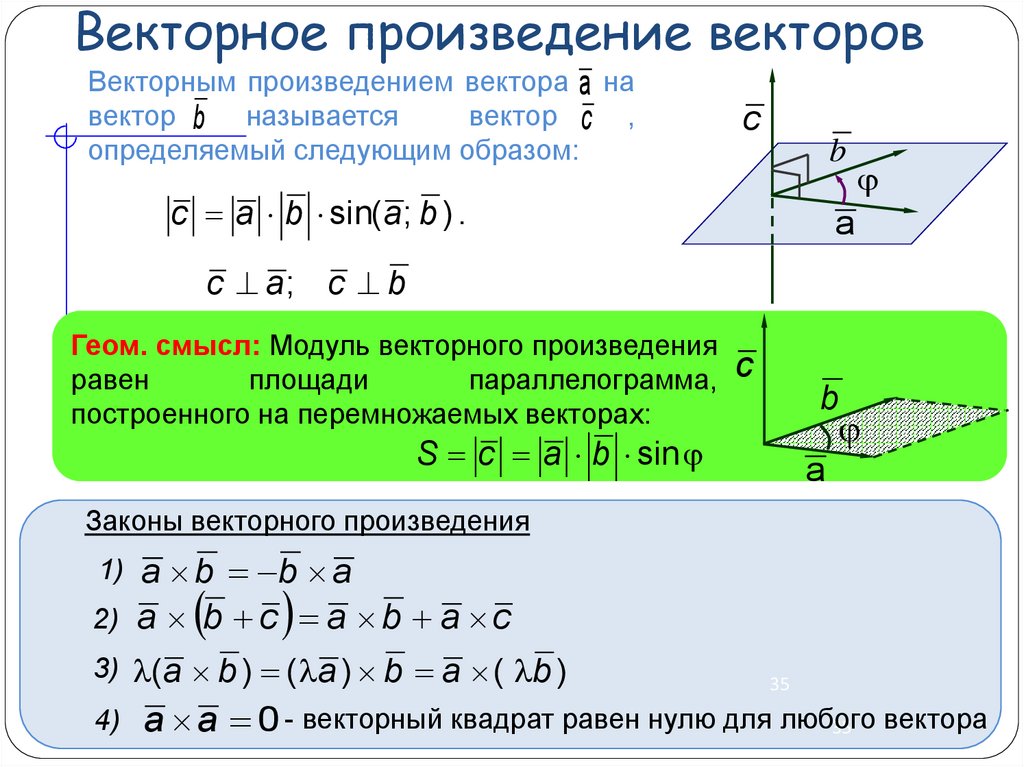
Если векторы параллельны, их векторное произведение равно нулю, что также может быть полезно для решения некоторых задач.
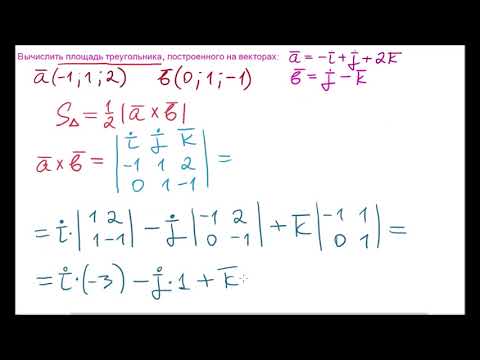
Площадь треугольника, построенного на векторах
Используйте графическое представление для лучшего понимания векторного произведения. Наглядно видно, как результат зависит от угла между векторами.

Убедитесь, что ваши векторы правильно ориентированы при вычислении векторного произведения, чтобы результат был точным и соответствовал геометрическому смыслу.