Основные методы нахождения уравнения прямой через точку с использованием различных формул
На данной странице представлены полезные советы и рекомендации по нахождению уравнения прямой, которая проходит через заданную точку. Эти методы полезны для студентов, изучающих геометрию, а также для тех, кто решает задачи на координатной плоскости. Мы рассмотрим основные подходы и ключевые формулы для нахождения уравнения прямой, используя точку и различные параметры.



Чтобы найти уравнение прямой через точку, начните с определения её координат, которые обозначаются как (x₁, y₁).

9 класс, 7 урок, Уравнение прямой

Используйте стандартную формулу уравнения прямой y - y₁ = m(x - x₁), где m — это угловой коэффициент прямой.
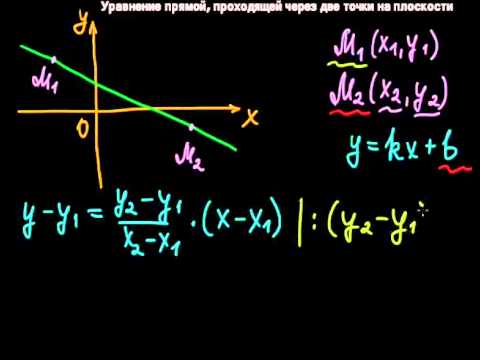
§11 Уравнение прямой, проходящей через две точки на плоскости


Если известен угловой коэффициент прямой, просто подставьте его в формулу, используя координаты точки.

Составляем уравнение прямой по точкам


Если прямую нужно выразить в виде y = kx + b, то вычислите b, подставив координаты точки и угловой коэффициент m.

Уравнение прямой проходящей через две точки. Урок геометрии 9 класс.


Если угловой коэффициент прямой не задан, используйте дополнительную информацию, например, другую точку на прямой.

Линейная функция: краткие ответы на важные вопросы - Математика - TutorOnline


В случае, если прямая вертикальная, её уравнение можно записать как x = x₁, где x₁ — абсцисса точки на прямой.

Математика без Ху%!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.

Если прямая горизонтальная, её уравнение будет иметь вид y = y₁, где y₁ — ордината точки на прямой.


Для нахождения углового коэффициента m, если дана ещё одна точка на прямой, используйте формулу m = (y₂ - y₁) / (x₂ - x₁).

Как составить уравнение прямой, проходящей через две точки. Урок 3. Геометрия 8 класс.
Запомните, что если прямая имеет вид y = mx + b, то для нахождения b нужно подставить координаты известной точки и вычислить свободный член.

Текстовые задачи №10 ЕГЭ и № 21 ОГЭ. Вебинар - Математика TutorOnline


Проверяйте полученные уравнения, подставляя координаты точки, чтобы удостовериться в их правильности.
