Тройные интегралы в цилиндрической системе координат: пошаговое руководство
Цилиндрическая система координат упрощает вычисление тройных интегралов в задачах с осевой симметрией. На этой странице вы найдете подробные примеры, полезные советы и объяснения для правильного применения этой системы в расчетах.
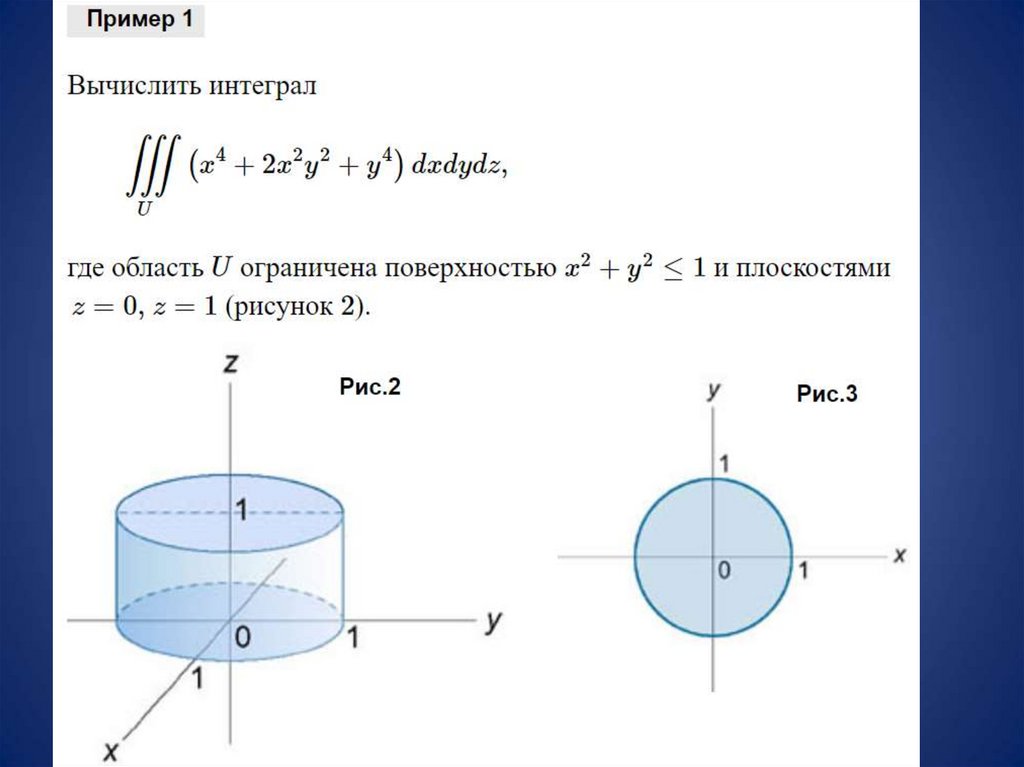

Перед началом работы определите границы интегрирования для каждой переменной (r, θ, z), учитывая геометрию области.

Объем через тройной интеграл в сферической системе координат

Всегда включайте якобиан (множитель r) в подынтегральное выражение при переходе к цилиндрическим координатам.

Тройной интеграл. Тройной интеграл в цилиндрических координатах

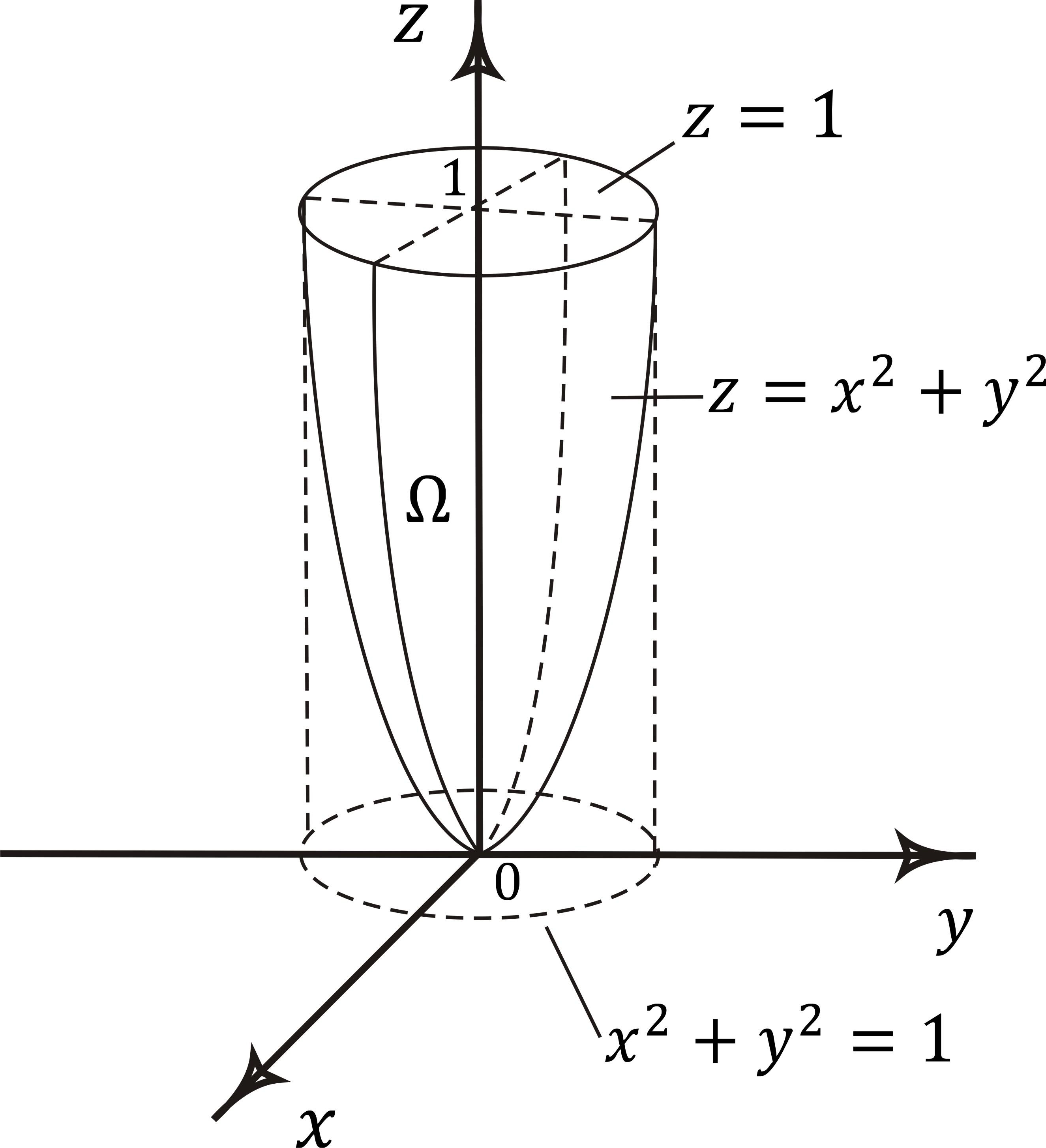
Обратите внимание, что угловая переменная θ измеряется в радианах, а не в градусах.
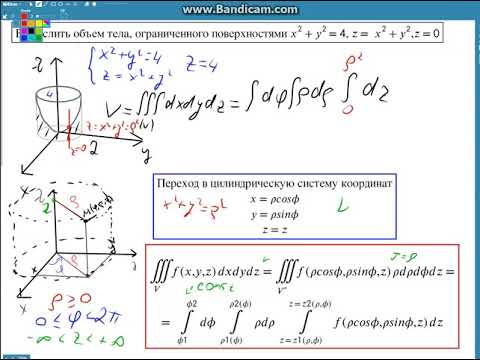
Для сложных областей используйте эскизы и визуализации, чтобы уточнить границы интегрирования.

Сферические координаты


Не забывайте проверять, соответствует ли функция под интегралом заданной симметрии области, что может значительно упростить вычисления.

Объем параболоида: тройной интеграл в цилиндрической системе координат

Если область симметрична относительно оси, рассмотрите упрощение интеграла через уменьшение углового диапазона (например, от 0 до π вместо 0 до 2π).

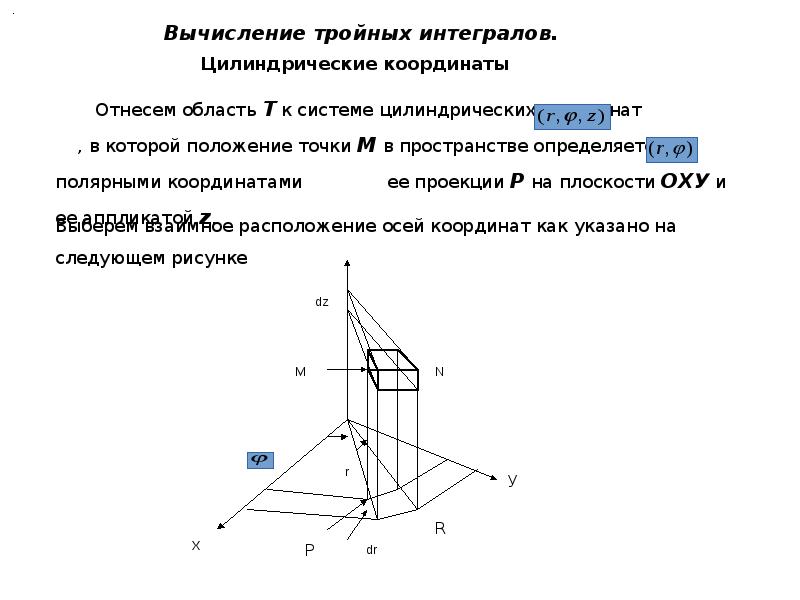
Разделяйте интегралы на несколько частей, если область определения функции разбивается на несколько областей с разными границами.

При необходимости обратитесь к математическим пакетам для проверки своих результатов или ускорения сложных вычислений.

Привыкайте преобразовывать интегралы в цилиндрических координатах обратно в декартовы для проверки.

Тройной интеграл в цилиндрических координатах.

Практикуйтесь на задачах с готовыми решениями, чтобы лучше понять алгоритм и специфику работы с цилиндрической системой координат.
